Flight Basics

Resources
A PDF of the 2016 lecture is found here. The original .pptx is here. The streaming video of the lecture may eventually be here. In the meantime, log on to Sakai, go to the HM ENGR80.X 2016 tab (where X is your section number, 1,2,3, or 4), click on the MediaSite link in the left navigation bar, if necessary click on the press here to launch link, and then watch the E80 - 2016S - Rm. Recital Hall_1/19/2016 video.
A PDF of the 2015 lecture is found here. The original .pptx is here. The streaming video of the lecture is here.
A PDF of the 2014 lecture is found here. The original .pptx is here.
A PDF of the 2013 lecture is found here.
A PDF of the 2012 lecture is found here.
Rocket Basics
The FAA has three classes of amateur rockets:
- Class 1 - a model rocket that uses no more than 125 grams (4.4 ounces) of propellant; uses a slow-burning propellant; is made of paper, wood, or breakable plastic; contains no substantial metal parts; and weighs no more than 1,500 grams (53 ounces) including the propellant – Requires permission of the Fire Department and the property owner.
- Class 2 – a high power rocket, other than a model rocket, that is propelled by a motor or motors having a combined total impulse of 40,960 Newton-seconds (9,208 pound-seconds) or less – Requires permission of FAA, Fire Department,
and property owner. Operator must also be TRA or NAR certified.
- Class 3 – an advanced high power rocket, other than a model rocket or high-power rocket – Has lots of regulatory restrictions.
Rockets flown in California require either State Fire Marshall certified motors or a bunch of permits.
Safety codes for Class 1 can be found here. Safety codes for Class 2 can be found here and here.
Modeling and Measurement of Rocket Performance
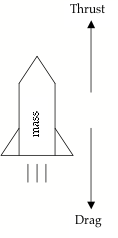
If mass change is small

A software package such as Rocksim has models for the mass,
thrust, and drag, and integrates Newton’s second law.
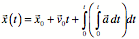
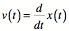
If you have 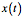 data (say from an altimeter) you can get velocity and
acceleration by numerically differentiating.
data (say from an altimeter) you can get velocity and
acceleration by numerically differentiating.
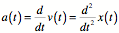
How do you take numerical derivatives? The straightforward
method is known as finite difference. There are two types, forward and
backward. For a set of data points 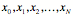
Forward Difference
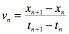
Backward Difference
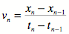
If the sample rate is constant the denominator can be
replaced with 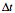 .
.
However, numerical derivatives amplify noise. There are a
number of methods for removing noise from numerical derivatives. Two common
ones are to:
- Low-pass filter either the signal, the derivatives, or both.
- Fit a smooth function, such as a polynomial or cubic spline to the data points and then analytically take the derivative of the fitting
function.
There are others.
Because numerically integrating reduces noise (but is
sensitive to drift) inertial measurement systems integrate accelerometers,
rather than differentiate position data. The best method uses a Kalman Filter
and uses data from acceleration, velocity, and position measurements.
Altimeter
A pressure-based altimeter measures the local absolute
pressure and uses a model for how the atmospheric pressure varies with altitude
to calculate the altitude. See details here. We are only interested in the expression from 0 km to 11 km in altitude. If your rocket manages to fly higher than 11 km we will be in big trouble with the FAA.
Inclinometer and Theodolite
An alternate method for measuring altitude is with one or
more inclinometers or theodolites.
An inclinometer measures angles relative to the horizontal.
A theodolite measures angles relative to both the horizontal and some baseline.
The method for using one inclinometer is explained here. A method for using two theodolites is
explained here and in much more detail here. Since it is unlikely that two projected lines would actually
intersect, one can also project two lines in 3-space and calculate the two
points on the lines where they are nearest each other. The basic equations are
found here. A Mathematica notebook of the derivation is found here.

![]()
![]()
![]() data (say from an altimeter) you can get velocity and
acceleration by numerically differentiating.
data (say from an altimeter) you can get velocity and
acceleration by numerically differentiating.![]()
![]()
![]()
![]()
![]()
![]() .
.

