Principal Component Analysis and Karhunen-Loeve Transform

We have discussed quite a few different orthogonal transforms, including Fourier transform, cosine transform, Walsh-Hadamard transform, Haar transform, etc., each of which, in its discrete form, is associated with an orthogonal (or unitary) matrix ${\bf A}$ that satisfies ${\bf A}^{-1}={\bf A}^T$ or ${\bf A}^T {\bf A}={\bf A}^{-1} {\bf A}={\bf I}$. This orthogonal matrix can be expressed in terms of its $N$ column vectors:

$${\bf A}=[{\bf a}_1,\cdots,{\bf a}_{N}],\;\;\;\;\;\mbox{or}\;\... ... {\bf a}_1^T \vdots {\bf a}^T_{N} \end{array} \right]$$

As these column vectors are orthonormal:

$$\langle{\bf a}_i, {\bf a}_j\rangle={\bf a}_i^T {\bf a}_j=\de... ...\{ \begin{array}{ll} 1 & i=j 0 & i\ne j\end{array} \right.$$

they form a set of $N$ orthogonal basis vectors to span an N-dimensional vector space.

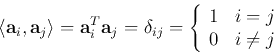
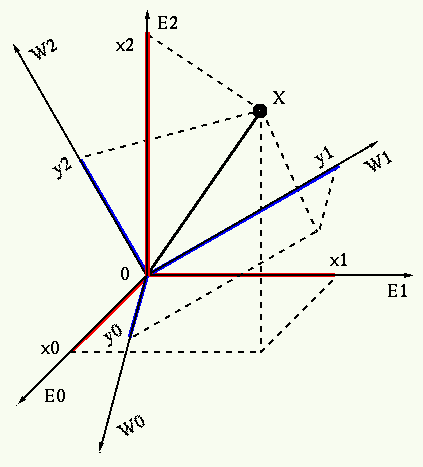
We have seen several times in the previous discussions of the various orthogonal transforms, the transform of any given discrete signal, represented as a vector in the N-dimensional space spanned by the standard basis vectors

$${\bf x}=\left[\begin{array}{c}x_1 \vdots x_N\end{array}\... ...+x_N\left[\begin{array}{c}0 \vdots 0 1\end{array}\right]$$

is carried out as a matrix multiplication:

$${\bf y}=\left[ \begin{array}{c}y_1 \vdots y_{N} \end{ar... ...}_1^T \vdots \\ {\bf a}^T_{N} \end{array} \right] {\bf x}$$

In the transform domain, the ith component of the vector $y_i={\bf a}_i^T {\bf x}$ is actually the projection of the signal vector ${\bf x}$ onto the ith basis vector ${\bf a}_i$. Left multiplying ${\bf A}$ on both sides of the transform equation above, we get the inverse transform:

$${\bf A}{\bf y}={\bf A}{\bf A}^T {\bf x}={\bf A}{\bf A}^{-1} {\bf x}={\bf x}$$

which can be rewritten as

$${\bf x}={\bf A}{\bf y}=[{\bf a}_1,\cdots,{\bf a}_{N}] \left[ ... ...ots y_{N} \end{array} \right] =\sum_{i=1}^{N} y_i {\bf a}_i$$

We see that the original signal vector ${\bf x}$ is expressed by the inverse transform as a linear combination of the orthogonal basis vectors ${\bf a}_i,\;(i=1,\cdots,N)$, the column vectors of the transform matrix. In other words, an orthogonal transform of the signal vector is actually a rotation in the N-dimensional space, represented by the orthogonal matrix, and different transform methods correspond to different rotations of the signal vector. In particular, the orthogonal transform matrix can be the identity matrix ${\bf A}={\bf I}=[{\bf e}_1,\cdots,{\bf e}_{N}]$ where ${\bf e}_i=[0,\cdots,0,1,0,\cdots,0]^T$ is the ith basis vector of the N-dimensional vector space. The transform associated with this matrix is ${\bf y}={\bf I}{\bf x}={\bf x}$, i.e., the coordinate system is not rotated.

In the previous chapters, we have also seen some specific applications of each of the transforms, such as various filtering in the transform domain (e.g., in frequency domain by Fourier transform and discrete cosine transform), such as encoding and data compression. Do all of these transforms, each represented by a totally different transform matrix from others, share some intrinsic properties and essential characteristics in common? Moreover, we may want to ask some more general questions, why do we want to carry out such transforms to start with? If an orthogonal transform is nothing more than a certain rotation of the signal vector in the N-dimensional space, what can be achieved by such a rotation? And, finally, is there a best rotation among all possible transform rotations (infinitely many of them)?

The following discussion for the principal component analysis (PCA) and the associated Karhunen-Loeve Transform (KLT) will answer all these questions.