


Next: Karhunen-Loeve Transform (KLT)
Up: klt
Previous: Multivariate Random Signals
Let 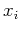 and
and 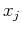 be two real random variables in a random vector
be two real random variables in a random vector
![${\bf x}=[x_1,\cdots,x_N]^T$](img45.png) .
The mean and variance of a variable
.
The mean and variance of a variable 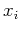 and the covariance and correlation coefficient
(normalized correlation) between two variables
and the covariance and correlation coefficient
(normalized correlation) between two variables 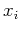 and
and 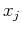 are defined below:
are defined below:
- Mean of
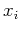 :
: 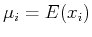
- Variance of
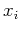 :
:
![$ \sigma^2_i=E[ (x_i-\mu_i)^2 ]=E(x_i^2)-m_i^2 $](img47.png)
- Covariance of
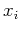 and
and 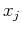 :
:
![$ \sigma^2_{ij}=E[ (x_i-\mu_i)(x_j-\mu_j) ]=E(x_ix_j)-\mu_i\mu_j $](img48.png)
- Correlation coefficient between
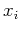 and
and 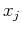 :
:
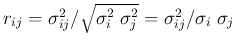
Note that the correlation coefficient
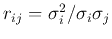 can be
considered as the normalized covariance
can be
considered as the normalized covariance 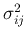 .
.
To obtain these parameters as expectations of the first and second order functions
of the random variables, the joint probability density function
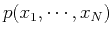 is required. However, when it is not available, the parameters can still be estimated
by averaging the outcomes of a random experiment involving these variables repeated
is required. However, when it is not available, the parameters can still be estimated
by averaging the outcomes of a random experiment involving these variables repeated
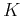 times:
times:
To understand intuitively the meaning of these parameters, we consider the following
very simple examples.
Examples:
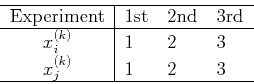
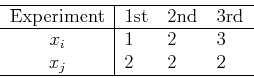
- Assume the experiment concerning
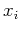 and
and 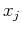 is repeated
is repeated 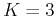 times with
the following outcomes:
times with
the following outcomes:
The means, variances and covariance of 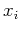 and
and 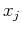 can be estimated as
can be estimated as
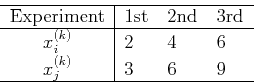
and the correlation coefficient is:
We see that 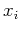 and
and 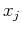 are highly (maximally in this case) correlated.
are highly (maximally in this case) correlated.
- Assume the outcomes of the 3 experiments are
then we have
and
We see that the two variables 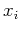 and
and 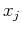 can be individually scaled while
their correlation remains the same.
can be individually scaled while
their correlation remains the same.
- Assume the outcomes of the 3 experiments are
We have
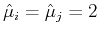 and
and
And the correlation coefficient is:
indicating that the two variables are highly inversely correlated.
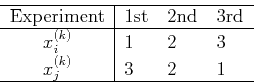
- Assume the outcomes are:
We have
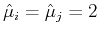 ,
,
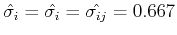 and
and
and 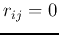 , indicating that the two variables are totally uncorrelated (unrelated).
, indicating that the two variables are totally uncorrelated (unrelated).
- Assume the experiment is carried out
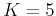 times with the outcomes:
times with the outcomes:
We still have
and 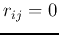 , indicating that the two variables are totally uncorrelated (unrelated).
, indicating that the two variables are totally uncorrelated (unrelated).
Now we see that the covariance 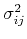 represents how much the two ramdom
variables
represents how much the two ramdom
variables 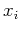 and
and 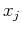 are positively correlated if
are positively correlated if
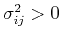 , negatively
correlated if
, negatively
correlated if
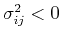 , or not correlated at all if
, or not correlated at all if
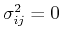 .
.
Assume a random vector
![${\bf x}=[x_1,\cdots,x_N]^T$](img45.png) is composed of
is composed of 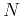 samples of a
signal
samples of a
signal 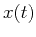 . The signal samples close to each other tend to be more correlated
than those that are farther away, i.e., given
. The signal samples close to each other tend to be more correlated
than those that are farther away, i.e., given 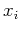 , we can predict the next sample
, we can predict the next sample
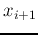 with much higher confidence than predicting some
with much higher confidence than predicting some 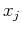 which is farther
away. Consequently, the elements in the covariance matrix
which is farther
away. Consequently, the elements in the covariance matrix 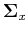 near the
main diagonal have higher values than those farther away from the diagonal.
near the
main diagonal have higher values than those farther away from the diagonal.



Next: Karhunen-Loeve Transform (KLT)
Up: klt
Previous: Multivariate Random Signals
Ruye Wang
2016-04-06
![]() and
and ![]() be two real random variables in a random vector
be two real random variables in a random vector
![]() .
The mean and variance of a variable
.
The mean and variance of a variable ![]() and the covariance and correlation coefficient
(normalized correlation) between two variables
and the covariance and correlation coefficient
(normalized correlation) between two variables ![]() and
and ![]() are defined below:
are defined below:
![]() is required. However, when it is not available, the parameters can still be estimated
by averaging the outcomes of a random experiment involving these variables repeated
is required. However, when it is not available, the parameters can still be estimated
by averaging the outcomes of a random experiment involving these variables repeated
![]() times:
times:
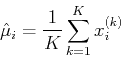
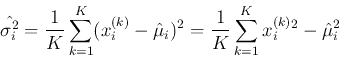
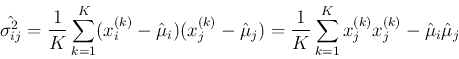
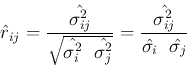
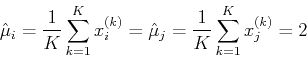
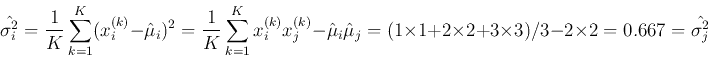
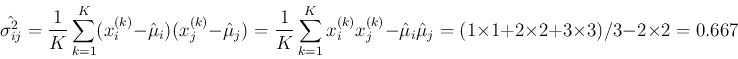
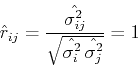
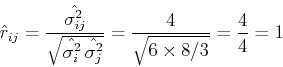
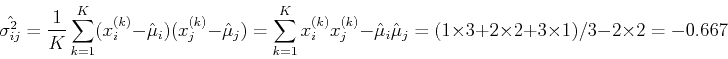
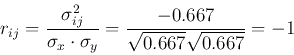

![]() is composed of
is composed of ![]() samples of a
signal
samples of a
signal ![]() . The signal samples close to each other tend to be more correlated
than those that are farther away, i.e., given
. The signal samples close to each other tend to be more correlated
than those that are farther away, i.e., given ![]() , we can predict the next sample
, we can predict the next sample
![]() with much higher confidence than predicting some
with much higher confidence than predicting some ![]() which is farther
away. Consequently, the elements in the covariance matrix
which is farther
away. Consequently, the elements in the covariance matrix ![]() near the
main diagonal have higher values than those farther away from the diagonal.
near the
main diagonal have higher values than those farther away from the diagonal.