


Next: KLT Completely Decorrelates the
Up: klt
Previous: Covariance and Correlation
Now we consider the Karhunen-Loeve Transform (KLT) (also known as Hotelling
Transform and Eigenvector Transform), which is closely related to the
Principal Component Analysis (PCA) and widely used in data analysis in many
fields.
Let 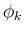 be the eigenvector corresponding to the kth eigenvalue
be the eigenvector corresponding to the kth eigenvalue 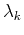 of the covariance matrix
of the covariance matrix 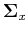 , i.e.,
, i.e.,
or in matrix form:
As the covariance matrix
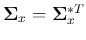 is Hermitian
(symmetric if
is Hermitian
(symmetric if 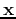 is real), its eigenvector
is real), its eigenvector 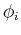 's are orthogonal:
's are orthogonal:
and we can construct an 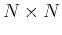 unitary (orthogonal if
unitary (orthogonal if 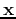 is real)
matrix
is real)
matrix 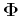
satisfying
The  eigenequations above can be combined to be expressed as:
eigenequations above can be combined to be expressed as:
or in matrix form:
Here 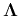 is a diagonal matrix
is a diagonal matrix
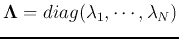 . Left multiplying
. Left multiplying
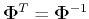 on both sides,
the covariance matrix
on both sides,
the covariance matrix 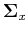 can be diagonalized:
can be diagonalized:
Now, given a signal vector 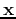 , we can define a unitary (orthogonal if
, we can define a unitary (orthogonal if 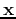 is real) Karhunen-Loeve Transform of
is real) Karhunen-Loeve Transform of 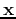 as:
as:
where the ith component 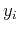 of the transform vector is the projection of
of the transform vector is the projection of 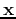 onto
onto 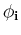 :
:
Left multiplying
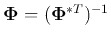 on both sides of the transform
on both sides of the transform
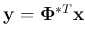 , we get the inverse transform:
, we get the inverse transform:
We see that by this transform, the signal vector 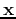 is now expressed in an
N-dimensional space spanned by the N eigenvectors
is now expressed in an
N-dimensional space spanned by the N eigenvectors 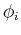 (
(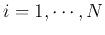 )
as the basis vectors of the space.
)
as the basis vectors of the space.



Next: KLT Completely Decorrelates the
Up: klt
Previous: Covariance and Correlation
Ruye Wang
2016-04-06
![]() be the eigenvector corresponding to the kth eigenvalue
be the eigenvector corresponding to the kth eigenvalue ![]() of the covariance matrix
of the covariance matrix ![]() , i.e.,
, i.e.,
![\begin{displaymath}\left[ \begin{array}{ccc}\cdots &\cdots &\cdots \\
\cdots & ...
...f\phi}_k \end{array} \right]
\;\;\;\;\;\;(k=1,\cdots,N) \end{displaymath}](img88.png)
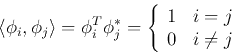
![\begin{displaymath}
\left[ \begin{array}{ccc}\ddots &\cdots &\cdots \\
\vdots &...
... & \vdots \\
0 & \cdots & \lambda_{N}
\end{array} \right]
\end{displaymath}](img97.png)
![\begin{displaymath}
{\bf y}=\left[ \begin{array}{c} y_1 \vdots y_{N} \end{...
...ht]\left[\begin{array}{c}x_1 \vdots, x_N\end{array}\right]
\end{displaymath}](img102.png)
![\begin{displaymath}
{\bf x}={\bf\Phi} {\bf y}=\left[\begin{array}{ccc}&& {\bf...
...dots y_{N} \end{array} \right]
=\sum_{i=1}^{N} y_i \phi_i
\end{displaymath}](img108.png)