Before reading on, it is highly recommended that you review the basics of multivariate probability theory
A real time signal ![]() can be considered as a random process and its samples
can be considered as a random process and its samples
![]() a random vector is the expectation of
a random vector is the expectation of ![]() :
:
![\begin{displaymath}
{\bf\Sigma}_x\stackrel{\triangle}{=}
E[ ({\bf x}-{\bf m}_x...
...^2 & \vdots \\
\cdots & \cdots & \ddots \end{array} \right]
\end{displaymath}](img23.png)
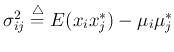 is the covariance
of two random variables
is the covariance
of two random variables
The correlation matrix of ![]() is defined as
is defined as
![\begin{displaymath}
{\bf R}_x\stackrel{\triangle}{=}E({\bf x}{\bf x}^{*T})
=\l...
...j} & \vdots \\
\cdots & \cdots & \ddots \end{array} \right]
\end{displaymath}](img31.png)
In general, if the data set ![]() is complex, both the covariance and the correlation
matrices are Hermitian, i.e.,
is complex, both the covariance and the correlation
matrices are Hermitian, i.e.,
A signal vector ![]() can always be easily converted into a zero-mean vector
can always be easily converted into a zero-mean vector
![]() with all of its dynamic energy (representing the
information contained) conserved. Without loss of generality for convenience,
sometimes we can assume
with all of its dynamic energy (representing the
information contained) conserved. Without loss of generality for convenience,
sometimes we can assume
![]() so that
so that
![]() .
.
After a certain orthogonal transform of a given random vector ![]() , the resulting
vector
, the resulting
vector
![]() is still random with the following mean and covariance:
is still random with the following mean and covariance: