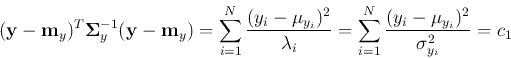Next: Comparison with Other Orthogonal
Up: klt
Previous: KLT Optimally Compacts Signal
Assume the N random variables in a signal vector
![${\bf x}=[x_1,\cdots, x_{N}]^T$](img167.png) have a normal joint probability density function:
have a normal joint probability density function:
where 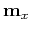 and
and 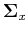 are the mean vector and covariance matrix of
are the mean vector and covariance matrix of
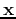 , respectively. When
, respectively. When 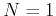 ,
, 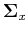 and
and 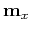 become
become
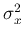 and
and 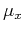 , respectively, and the density function becomes the
familiar single variable normal distribution:
, respectively, and the density function becomes the
familiar single variable normal distribution:
The shape of this normal distribution in the N-dimensional space can be represented
by the iso-hypersurface in the space determined by equation
where 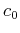 is a constant. Or, equivalently, this equation can be written as
is a constant. Or, equivalently, this equation can be written as
where 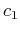 is another constant related to
is another constant related to 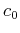 ,
, 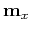 and
and 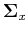 .
.
In particular, when 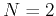 ,
,
![${\bf x}=[x_1, x_2]^T$](img178.png) , and we assume
, and we assume
then the equation above becomes
As 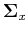 is positive definite, and so is
is positive definite, and so is
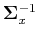 , we have
, we have
i.e., the quadratic equation above represents an ellipse (instead of other quadratic
curves such as hyperbola and parabola) centered at
![${\bf m}_x=[\mu_1, \mu_2]^T$](img185.png) .
When
.
When 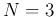 , the quadratic equation represents an ellipsoid. In general when
, the quadratic equation represents an ellipsoid. In general when
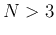 , the equation
, the equation
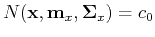 represents a
hyper ellipsoid in the N-dimensional space. The center and spatial distribution
of this ellipsoid are determined by
represents a
hyper ellipsoid in the N-dimensional space. The center and spatial distribution
of this ellipsoid are determined by 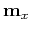 and
and 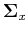 , respectively.
, respectively.
By the KLT, the signal
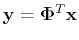 is completely decorrelated
and its the covariance matrix becomes diagonalized:
is completely decorrelated
and its the covariance matrix becomes diagonalized:
and the isosurface equation
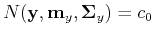 becomes
becomes
This equation represents a standard hyper-ellipsoid in the N-dimensional space.
In other words, the KLT
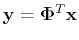 rotates the coordinate
system so that the semi-principal axes of the ellipsoid represented by
rotates the coordinate
system so that the semi-principal axes of the ellipsoid represented by
 are in parallel with
are in parallel with 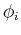 (
(
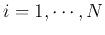 ), the axes of the new coordinate system. Moreover, the length
of the semi-principal axis parallel to
), the axes of the new coordinate system. Moreover, the length
of the semi-principal axis parallel to 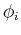 is proportional to
is proportional to
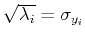 .
.
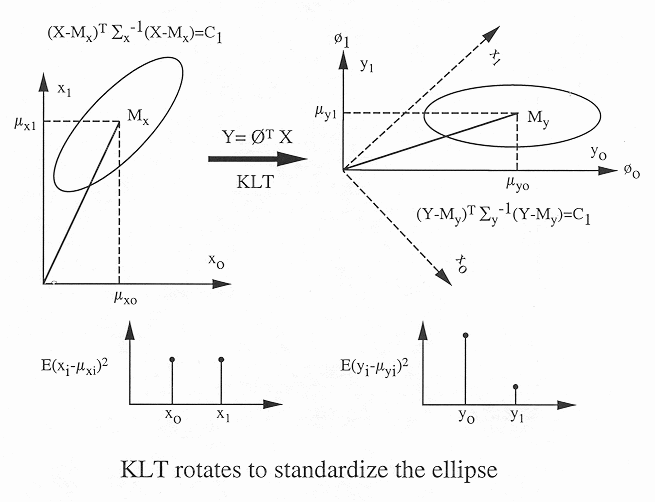
The standardization of the ellipsoid is the essential reason why the rotation of
KLT can achieve two highly desirable outcomes: (a) the decorrelation of the signal
components, and (b) redistribution and compaction of the energy or information
contained in the signal, as illustrated in the figure:



Next: Comparison with Other Orthogonal
Up: klt
Previous: KLT Optimally Compacts Signal
Ruye Wang
2016-04-06
![]() have a normal joint probability density function:
have a normal joint probability density function:
![\begin{displaymath}
p(x_1,\cdots, x_{N})=p({\bf x})=N({\bf x}, {\bf m}_x, {\bf\S...
...bf x}-{\bf m}_x)^T{\bf\Sigma}_x^{-1}({\bf x}-{\bf m}_x)\right]
\end{displaymath}](img168.png)
![\begin{displaymath}
p(x)=N(x,\mu_x, \sigma_x)
=\frac{1}{\sqrt{2\pi \sigma_x^2}}\;exp\left[-\frac{(x-\mu_x)^2}{2\sigma_x^2}\right]
\end{displaymath}](img172.png)
![]() ,
,
![]() , and we assume
, and we assume
![\begin{displaymath}
{\bf\Sigma}_x^{-1}=\left[ \begin{array}{cc} A & B/2 B/2 & C \end{array} \right]
\end{displaymath}](img179.png)
![$\displaystyle [x_1-\mu_{x_1}, x_2-\mu_{x_2}]
\left[ \begin{array}{cc} A & B/2 ...
...]
\left[ \begin{array}{c} x_1-\mu_{x_1} x_2-\mu_{x_2} \end{array} \right]$](img181.png)
![]() is completely decorrelated
and its the covariance matrix becomes diagonalized:
is completely decorrelated
and its the covariance matrix becomes diagonalized:
![\begin{displaymath}
{\bf\Sigma}_y ={\bf\Lambda}=
\left[ \begin{array}{ccc}
\la...
... \vdots \\
0 & \cdots & \sigma^2_{y_{N}} \end{array} \right]
\end{displaymath}](img189.png)