


Next: KLT Optimally Compacts Signal
Up: klt
Previous: Karhunen-Loeve Transform (KLT)
Now we show that among all possible orthogonal transforms, KLT is optimal in the
following sense:
- KLT completely decorrelates the signal
- KLT maximally compacts the energy (information) contained in the signal.
The first property is simply due to the definition of KLT, and the second
property is due to the fact that KLT redistributes the energy among the 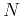 components in such a way that most of the energy is contained in a small number
of components of
components in such a way that most of the energy is contained in a small number
of components of
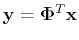 , as we will show later.
, as we will show later.
To see the first property, consider the mean vector  and covariance
matrix
and covariance
matrix 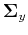 of
of
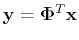 :
:
The above can also be written in matrix form:
We can make two observations:
- After KLT, the covariance matrix of the signal
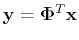 is diagonalized, i.e., the covariance
is diagonalized, i.e., the covariance 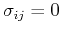 between any two components
between any two components
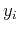 and
and 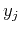 is always zero. In other words, the signal is completely decorrelated.
is always zero. In other words, the signal is completely decorrelated.
- The variance of
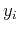 is the same as the ith eigenvalue of the covariance
matrix of
is the same as the ith eigenvalue of the covariance
matrix of 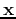 , i.e.,
, i.e.,
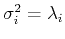 .
.



Next: KLT Optimally Compacts Signal
Up: klt
Previous: Karhunen-Loeve Transform (KLT)
Ruye Wang
2016-04-06
![]() and covariance
matrix
and covariance
matrix ![]() of
of
![]() :
:
![\begin{displaymath}
{\bf\Sigma}_y
=\left[ \begin{array}{ccc}
\cdots & \cdots &...
... & \vdots \\
0 & \cdots & \sigma^2_{{N}} \end{array} \right]
\end{displaymath}](img117.png)