


Next: Geometric Interpretation of KLT
Up: klt
Previous: KLT Completely Decorrelates the
Now we show that KLT redistributes the energy contained in the signal so that it is
maximally compacted into a small number of components after the KLT transform.
Let 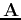 be an arbitrary orthogonal matrix satisfying
be an arbitrary orthogonal matrix satisfying
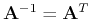 ,
and we represent
,
and we represent 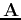 in terms of its column vectors
in terms of its column vectors
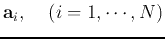 as
as
Based on this matrix  , an orthogonal transform of a given signal vector
, an orthogonal transform of a given signal vector 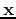 can be defined as
can be defined as
The inverse transform is:
Now we consider the variances of the signal components before and after the KLT
transform:
where
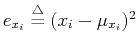 can be considered as the dynamic
energy or information contained in the ith component of the signal, and the trace of
the covariance matrix
can be considered as the dynamic
energy or information contained in the ith component of the signal, and the trace of
the covariance matrix
 represents the total energy
represents the total energy 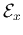 or
information contained in the signal
or
information contained in the signal 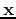 :
:
Due to the commutativity of trace:
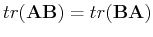 , we have:
, we have:
reflecting the fact that the total energy or information of the signal is conserved
after the KLT transform, or any unitary (orthogonal) transform (Parseval's theorem.
However, the energy distribution among all 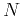 components can be very different
before and after the KLT transform, as shown below.
components can be very different
before and after the KLT transform, as shown below.
We define the energy contained in the first  components after the transform
components after the transform
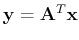 as
as
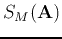 is a function of the transform matrix
is a function of the transform matrix 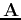 .
Since the total energy is conserved,
.
Since the total energy is conserved, 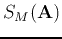 is also proportional to the
percentage of energy contained in the first
is also proportional to the
percentage of energy contained in the first  components.
In the following we will show that
components.
In the following we will show that 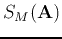 is maximized if and only if the
transform matrix is the same as that of the KLT:
is maximized if and only if the
transform matrix is the same as that of the KLT:
In other words, the KLT optimally compacts energy into a few components of the
signal. Consider
Now we need to find a transform matrix
![${\bf A}=[{\bf a}_1,\cdots,{\bf a}_N]$](img142.png) , so that
, so that
The constraint
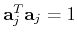 is to guarantee that the column vectors
in
is to guarantee that the column vectors
in 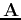 are normalized. This constrained optimization problem can be solved
using Lagrange multiplier method by letting the following partial derivative be zero:
are normalized. This constrained optimization problem can be solved
using Lagrange multiplier method by letting the following partial derivative be zero:
(* The last equal sign is due to explanation in the
review of linear algebra.)
We see that the column vectors of 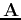 must be the eigenvectors of
must be the eigenvectors of 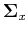 :
:
i.e.,
 has to be an eigen-vector of
has to be an eigen-vector of 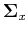 , and the
transform matrix must be
, and the
transform matrix must be
where 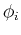 's are the orthogonal eigenvectors of
's are the orthogonal eigenvectors of 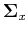 corresponding
to eigenvalues
corresponding
to eigenvalues  (
(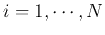 ):
):
Thus we have proved that the optimal transform is indeed KLT, and
where the ith eigenvalue  of
of 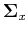 is also the average (expectation)
energy contained in the ith component of the signal. If we choose those
is also the average (expectation)
energy contained in the ith component of the signal. If we choose those
 that correspond to the
that correspond to the 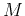 largest eigenvalues of
largest eigenvalues of 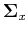 :
:
 ,
then
,
then
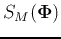 will be maximized.
will be maximized.
Due to KLT's properties of signal decorrelation and energy compaction, it can
be used for data compression by reducing the dimensionality of the data set.
Specifically, we carry out the following steps:
- Find the mean vector
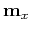 and the covariance matrix
and the covariance matrix 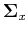 of the signal vectors
of the signal vectors 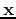 .
.
- Find the eigenvalues
 ,
,  ) of
) of 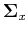 ,
sorted in descending order, and their corresponding eigenvectors
,
sorted in descending order, and their corresponding eigenvectors 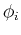
 ).
).
- Choose a lowered dimensionality
 so that the percentage of energy contained
is no less than a given threshold (e.g., 95%):
so that the percentage of energy contained
is no less than a given threshold (e.g., 95%):
- Construct an
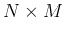 transform matrix composed of the
transform matrix composed of the 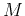 largest eigenvectors
of
largest eigenvectors
of 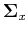 :
:
and carry out KLT based on  :
:
As the dimension 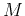 of
of  is less than the dimension
is less than the dimension 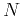 of
of 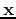 , data
compression is achieved for storage or transmission. This is a lossy compression with
the error representing the percentage of information lost:
, data
compression is achieved for storage or transmission. This is a lossy compression with
the error representing the percentage of information lost:
 . But as these
. But as these  's
for
's
for
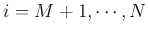 are the smallest eigenvalues, the error is minimized
(e.g., 5%).
are the smallest eigenvalues, the error is minimized
(e.g., 5%).
- Reconstruct
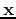 by inverse KLT:
by inverse KLT:



Next: Geometric Interpretation of KLT
Up: klt
Previous: KLT Completely Decorrelates the
Ruye Wang
2016-04-06
![]() be an arbitrary orthogonal matrix satisfying
be an arbitrary orthogonal matrix satisfying
![]() ,
and we represent
,
and we represent ![]() in terms of its column vectors
in terms of its column vectors
![]() as
as
![\begin{displaymath}{\bf A}=[{\bf a}_1, \cdots, {\bf a}_{N}],\;\;\;\;\;\;\mbox{or...
...{\bf a}_1^{T} \vdots {\bf a}_{N}^{T} \end{array} \right] \end{displaymath}](img123.png)
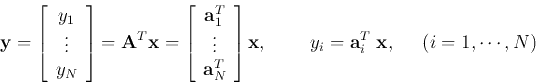
![\begin{displaymath}{\bf x}={\bf A}{\bf y}=[{\bf a}_1,\cdots,{\bf a}_{N}]
\left[ ...
...ots y_{N} \end{array} \right]
=\sum_{i=1}^{N} y_i {\bf a}_i \end{displaymath}](img13.png)
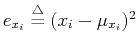 can be considered as the dynamic
energy or information contained in the ith component of the signal, and the trace of
the covariance matrix
can be considered as the dynamic
energy or information contained in the ith component of the signal, and the trace of
the covariance matrix
![\begin{displaymath}
{\cal E}_x= tr {\bf\Sigma}_x
=\sum_{i=1}^{N} \sigma_{x_i}^2=\sum_{i=1}^{N} E[({x_i}-\mu_{x_i})^2]
=\sum_{i=1}^{N}E(e_{x_i})
\end{displaymath}](img130.png)
![]() , we have:
, we have:
![]() components after the transform
components after the transform
![]() as
as
![\begin{displaymath}
S_M({\bf A})\stackrel{\triangle}{=}\sum_{i=1}^{M} E\left[(y_...
...right]
=\sum_{i=1}^{M}\sigma_{y_i}^2=\sum_{i=1}^{M}E(e_{y_i})
\end{displaymath}](img134.png)
![$\displaystyle \sum_{i=1}^{M} E(y_i-\mu_{y_1})^2
=\sum_{i=1}^{M} E\left[ {\bf a}_i^{T}({\bf x}-{\bf m}_{x_i})\;({\bf x}-{\bf m}_{x_i})^T{\bf a}_i \right]$](img140.png)
![$\displaystyle \sum_{i=1}^{M} {\bf a}_i^{T}E\left[({\bf x}-{\bf m}_{x_i}) ({\bf ...
...)^T\right] {\bf a}_i^{T}
=\sum_{i=1}^{M} {\bf a}_i^{T} {\bf\Sigma}_x {\bf a}_i$](img141.png)
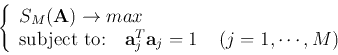
![$\displaystyle \frac{\partial}{\partial {\bf a}_i}\left[S_M({\bf A})-\sum_{j=1}^...
...j^{T}{\bf\Sigma}_x{\bf a}_j-\lambda_j {\bf a}_j^{T}{\bf a}_j+\lambda_j) \right]$](img145.png)

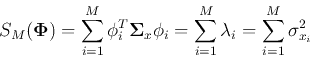

![\begin{displaymath}
{\bf y}=\left[ \begin{array}{c} y_1 \vdots y_{M} \end{...
...\vdots \vdots x_{N}
\end{array} \right]_{N \times 1}
\end{displaymath}](img162.png)
![\begin{displaymath}{\bf x}=\left[ \begin{array}{c} x_1 \vdots \vdots x_{...
...{c} y_1 \vdots y_{M}
\end{array} \right]_{M \times 1}
\end{displaymath}](img166.png)