Next: Softmax Regression for Multiclass Up: Regression Analysis and Classification Previous: Nonlinear Least Squares Regression
All previously discussed regression methods can be considered
as supervised binary classifiers, when the regression function








if then then |
(207) |
 , it
becomes an equation
, it
becomes an equation
 representing a hypersurface
in the d-dimensional space (a point if
representing a hypersurface
in the d-dimensional space (a point if  , a curve if
, a curve if  ,
a surface or hypersurfaceif
,
a surface or hypersurfaceif  ), by which the space is
partitioned into two regions. In this case,
), by which the space is
partitioned into two regions. In this case,
 is
called the decision function and the surface
decision boundary. Now any point in the space is classified
into either of the two classes, depending on whether it is on the
positive side of the decision boundary (
is
called the decision function and the surface
decision boundary. Now any point in the space is classified
into either of the two classes, depending on whether it is on the
positive side of the decision boundary (
 ) or the
negative side (
) or the
negative side (
 ).
).
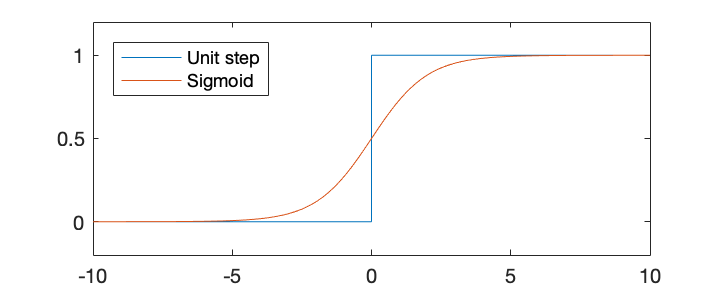
This simple binary classifier suffers from the drawback that
the distance between a point 

This problem can be addressed by the method of
logistic regression, which is similarly trained based
on the training set with each sample 












Similar to linear and nonlinear regression methods considered
before, the goal of logistic regression is also to find the
optimal model parameter



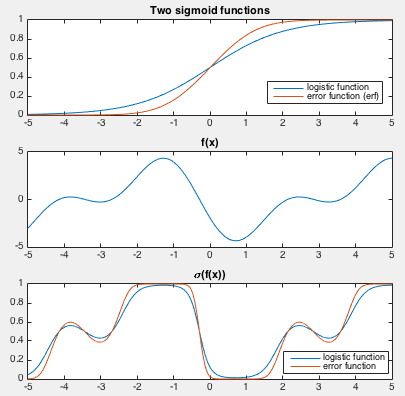
The sigmoid function can be either the error function (cumulative Gaussian, erf):
 |
(208) |
 |
|||
 |
|||
 |
(210) |
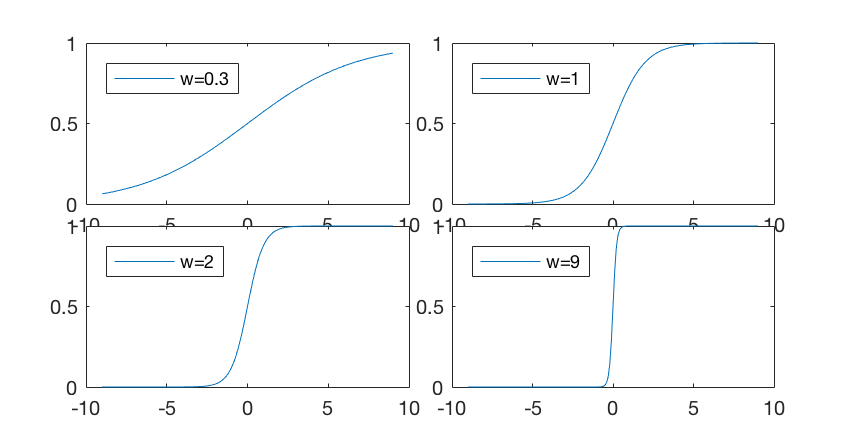
 can be included in the logistic function
to control its softness when used to threshold the variable
can be included in the logistic function
to control its softness when used to threshold the variable  as
shown below:
as
shown below:
 |
(211) |
 is thresholded by the logistic
function with variable softness controlled by parameter
is thresholded by the logistic
function with variable softness controlled by parameter  ,
between the two extreme cases of
,
between the two extreme cases of
 (no
thresholding) when
(no
thresholding) when  , and
, and
 when
when
 (hard thresholding).
(hard thresholding).
Now the function value




 , i.e.,
, i.e.,  is
far away from the plane
is
far away from the plane
 on the positive side,
then the probability
on the positive side,
then the probability
 is close to 1;
is close to 1;
 , i.e.,
, i.e.,  is
far away from the plane
is
far away from the plane
 on the negative side,
then the probability
on the negative side,
then the probability
 is close to 0, but
is close to 0, but
 for
for
 is close to 1;
is close to 1;
 , i.e.,
, i.e.,  is close
to the plane
is close
to the plane
 , then
, then
 , and
, and
 , i.e.,
the probability for
, i.e.,
the probability for  to belong to either
to belong to either  or
or
 is about the same.
is about the same.
The value of the logistic function is interpreted as the
conditional probability of output 


 is:
is:
 |
(213) |
 (either 1 or 0), as the labeling of a sample
(either 1 or 0), as the labeling of a sample
 in the training set:
in the training set:
 |
 |
 |
(214) |
 given all
given all
 samples in
samples in
 (assumed i.i.d.):
(assumed i.i.d.):
 |
 |
 |
|
 |
 |
(215) |
 can be defined as the
one that maximizes the likelihood function
can be defined as the
one that maximizes the likelihood function
 ,
or, equivalently, that minimizes the negative log likelihood as
the objective function:
This is the method of maximum likelihood estimation (MLE), and
it produces the most probable estimation of certan parameter
of a model based on the given data.
,
or, equivalently, that minimizes the negative log likelihood as
the objective function:
This is the method of maximum likelihood estimation (MLE), and
it produces the most probable estimation of certan parameter
of a model based on the given data.
The optimal paramter 
 |
(217) |
 is
the likelihood found above,
is
the likelihood found above,
 is the prior probability
of
is the prior probability
of  without observing the training data
without observing the training data  , and
the denominator independent of the variable
, and
the denominator independent of the variable  is dropped
as a constant independent of
is dropped
as a constant independent of  .
.
Based on the assumption that all components of 
 |
(218) |
 is
independent of
is
independent of  and is therefore dropped. The
assumed zero mean is due to the desire that the values of
all weights in
and is therefore dropped. The
assumed zero mean is due to the desire that the values of
all weights in  should be around zero instead
of large values on either positive or negative side, to
avoid overfitting, as discussed below.
should be around zero instead
of large values on either positive or negative side, to
avoid overfitting, as discussed below.
Now the posterior can be written as
 that maximizes this posterior
that maximizes this posterior
 by the mathod
of maximum a posteriori (MAP) estimation. To do so, we
minimize the negative log posterior as the objective function:
by the mathod
of maximum a posteriori (MAP) estimation. To do so, we
minimize the negative log posterior as the objective function:
 as a hyperparameter in
the second term
as a hyperparameter in
the second term
 treated as a penalty
term to discourage large values of
treated as a penalty
term to discourage large values of  , similar to
Eq. (142) for ridge regression. A larger
value of
, similar to
Eq. (142) for ridge regression. A larger
value of  will result in smaller values for
will result in smaller values for  ,
and the logistic function will be more smooth for softer
thresholding, and the classification is less affected by
possible noisy outliers close to the decision boundary. In
other words, by adjusting
,
and the logistic function will be more smooth for softer
thresholding, and the classification is less affected by
possible noisy outliers close to the decision boundary. In
other words, by adjusting  , we can make a proper
tradeoff between overfitting and underfitting.
, we can make a proper
tradeoff between overfitting and underfitting.
In particular, if







Now we can find the optimal 


![$\displaystyle {\bf r}={\bf r}({\bf w})=\left[\begin{array}{c}r_1({\bf w})\\
\v...
...w}^T{\bf x}_1)-y_1\\ \vdots\\
\sigma({\bf w}^T{\bf x}_N)-y_N\end{array}\right]$](img1023.svg) |
(222) |
 residuals
residuals
 , the difference between the model prediction
, the difference between the model prediction
 and the ground truth labeling
and the ground truth labeling
 . Based on
. Based on
 we can find the
optimal
we can find the
optimal  that minimizes this objective function iteratively
by the gradient descent method.
We note that the gradient in Eq. (221)
is based on all
that minimizes this objective function iteratively
by the gradient descent method.
We note that the gradient in Eq. (221)
is based on all  training samples in the training set. If
training samples in the training set. If  is
large, then the stochastic gradient descent method can be considered
based on only one of the
is
large, then the stochastic gradient descent method can be considered
based on only one of the  samples in each iteration.
samples in each iteration.
Below is a segment of Matlab code for estimating 
X contains the 

y contains the corresponding
a binary labelings.
The following code segment estimates weight vector 
X=[ones(1,n); X]; % augmented X with x_0=1
w=ones(m+1,1); % initialize weight vector
g=X*(sgm(w,X)-y)'; % gradient of log posterior
tol=10^(-6); % tolerance
delta=0.1; % step size
while norm(g)>tol % terminate when gradient is small enough
w=w-delta*g; % update weight vector by gradient descent
g=X*(sgm(w,X)-y)'; % update gradient
end
where
function s=sgm(w,X)
s=1./(1+exp(-w'*X));
end
Alternatively, this minimization problem for finding
optimal 


 |
 |
 |
|
 |
![$\displaystyle {\bf X}\frac{d}{d{\bf w}}\left[\begin{array}{c}
r_1({\bf w})\\ \vdots\\ r_N({\bf w})\end{array}\right]
+\lambda
={\bf X}{\bf J}_r({\bf w})+\lambda$](img1032.svg) |
(223) |
 is the
is the
 Jacobian matrix
of the vector function
Jacobian matrix
of the vector function
 , whose nth row is
, whose nth row is
![$\displaystyle \frac{dr_n({\bf w})}{d{\bf w}} =\frac{d}{d{\bf w}}
\left[\sigma({...
...\sigma({\bf w}^T{\bf x}_n)[1-\sigma({\bf w}^T{\bf x}_n)]{\bf x}_n
=z_n{\bf x}_n$](img1035.svg) |
(224) |
 ,
which is always greater than zero as
,
which is always greater than zero as
 .
Now the Jacobian can be written as
.
Now the Jacobian can be written as
![$\displaystyle {\bf J}_r({\bf w})=\left[\begin{array}{c}dr_1({\bf w})/d{\bf w}\\...
...array}{c}{\bf x}_1^T\\ \vdots\\ {\bf x}_N^T\end{array}\right]
={\bf Z}{\bf X}^T$](img1037.svg) |
(225) |
 is a positive definite diagonal
matrix (as
is a positive definite diagonal
matrix (as  ). Substituting
). Substituting  back into the expression
for
back into the expression
for
 above, we get
above, we get
 |
(226) |
Since 

 |
(227) |
 is also positive definite, and the objective
function
is also positive definite, and the objective
function
 when approximated by the first three terms of
its Taylor series is has a global minimum.
when approximated by the first three terms of
its Taylor series is has a global minimum.
Having found



 |
(228) |
 by
Newton method:
by
Newton method:
X=[ones(1,n); X]; % augmented X with x_0=1
w=ones(m+1,1); % initialize weight vector
g=X*(sgm(w,X)-y)'; % gradient of log posterior
H=X*diag(s.*(1-s))*X'; % Hesian of log posterior
tol=10^(-6)
while norm(g)>tol % terminate when gradient is small enough
w=w-inv(H)*g; % update weight vector by Newton-Raphson
s=sgm(w,X); % update sigma
g=X*(s-y)'; % update gradient
H=X*diag(s.*(1-s))*X'; % update Hessian
end
Once the model parameter 




In summary, we make a comparison between the linear and logistic
regression methods both can be used for binary classification. In
linear regression, the function value












