In linear regression, the relationship between the dependent
variable  and
and  independent variables in
independent variables in
![${\bf x}=[x_1,\cdots,x_d]^T$](img491.svg) is modeled by a linear hypothesis
function:
is modeled by a linear hypothesis
function:
 |
(108) |
where
![${\bf x}=[x_0=1,x_1,\cdots,x_d]^T$](img559.svg) is redefined as an
augmented
is redefined as an
augmented  dimensional vector containing
dimensional vector containing  as well as
the
as well as
the  independent variables, and
independent variables, and
![${\bf w}=[w_0=b,w_1,\cdots,w_d]^T$](img561.svg) is an argmented
is an argmented  dimensional vector containing
dimensional vector containing  as
well as the
as
well as the  weights as the parameters, to be determined
based on the given dataset.
weights as the parameters, to be determined
based on the given dataset.
Geometrically, this linear regression function
 is a straight line if
is a straight line if  ,
a plane if
,
a plane if  , or a hyperplane if
, or a hyperplane if  , in the
, in the  dimensional
space spanned by
dimensional
space spanned by  as well as
as well as
 . The
function has an
intercept
. The
function has an
intercept
 along the
along the  dimension and a normal
direction
dimension and a normal
direction
![$[w_1,\cdots,w_d,\,-1]^T$](img565.svg) . When thresholded by the plane
. When thresholded by the plane
 , the regression function becomes an equation
, the regression function becomes an equation
 , representing a point if
, representing a point if  , a
straight line if
, a
straight line if  , a plane or hyperplane if
, a plane or hyperplane if  , in the
d-dimensional space spanned by
, in the
d-dimensional space spanned by
 , as shown in
the figure below for
, as shown in
the figure below for  .
.
We denote by  the matrix containing the
the matrix containing the  augmented data
points
augmented data
points
![${\bf x}_n=[x_{0n}=1,\,x_{1n},\cdots,x_{dn}]^T\;(n=1,\cdots,N)$](img569.svg) as its column vectors
as its column vectors
![$\displaystyle {\bf X}=\left[\begin{array}{ccc}1 &\cdots&1\\ x_{11}&\cdots&x_{1N...
...}&\cdots&x_{dN}\end{array}\right]_{(d+1)\times N}
=[{\bf x}_1,\cdots,{\bf x}_N]$](img570.svg) |
(109) |
and its transpose can be written as:
![$\displaystyle {\bf X}^T=\left[\begin{array}{cccc}1 & x_{11} & \cdots & x_{d1}
\...
...imes(d+1)}
=\left[{\bf 1},\underline{\bf x}_1,\cdots,\underline{\bf x}_d\right]$](img571.svg) |
(110) |
where
![${\bf 1}=[1,\cdots,1]^T$](img572.svg) , and
, and
![$\underline{\bf x}_i=[x_{i1},\cdots,x_{iN}]^T\;\;(i=1,\cdots,d)$](img573.svg) is
an N-dimensional vectors containing the ith components of all
is
an N-dimensional vectors containing the ith components of all
 data vectors in the dataset.
data vectors in the dataset.
Now the linear regression problem is simply to find the model
parameter, here the weight vector  , so that the model
prediction
, so that the model
prediction
 |
(111) |
matches the ground truth labeling  . In other words,
the residual of the linear model defined as
. In other words,
the residual of the linear model defined as
 need to be zero:
need to be zero:
 |
(112) |
This is a linear system containing  equations of
equations of  unknowns.
unknowns.
If the number of data samples is equal to the number of unknown
parameters, i.e.,  , then
, then  is a square and
invertible matrix (assuming all
is a square and
invertible matrix (assuming all  samples are independent and
therefore
samples are independent and
therefore  has a full rank), and the equation above can
be solved to get the desired weight vector:
has a full rank), and the equation above can
be solved to get the desired weight vector:
 |
(113) |
However, as typically  , i.e., there are many more data
samples than the unknown parameters,
, i.e., there are many more data
samples than the unknown parameters,  is non-invertible
and
is non-invertible
and
 is over-determined linear system
without a solution, i.e, the prediction
is over-determined linear system
without a solution, i.e, the prediction
 can never match the ground truth labeling
can never match the ground truth labeling  . We need to
find an optimal solution
. We need to
find an optimal solution  that minimizes the SSE
(proportional to MSE):
that minimizes the SSE
(proportional to MSE):
To find the optimal  that minimizes
that minimizes
 ,
we set the gradient of
,
we set the gradient of
 to zero and get the
normal equation:
to zero and get the
normal equation:
 i.e. i.e. |
(115) |
Solving for  , we get the optimal weight vector:
, we get the optimal weight vector:
 |
(116) |
where
 is the
is the
 pseudo-inverse
of the
pseudo-inverse
of the
 matrix
matrix  .
This method for estimating the regression model parameters is
called ordinary least squares (OLS).
.
This method for estimating the regression model parameters is
called ordinary least squares (OLS).
Having found the parameter  for the linear regression
model
for the linear regression
model
 , we can predict the outputs
corresponding to any unlabed test dataset
, we can predict the outputs
corresponding to any unlabed test dataset
![${\bf X}_*=[{\bf x}_{1*},\cdots,{\bf x}_{M*}]$](img597.svg) :
:
![$\displaystyle \hat{\bf y}_*={\bf f}_*={\bf X}_*^T{\bf w}^*
=[{\bf 1},\underline...
...s\\ w^*_d\end{array}\right]
=w^*_0{\bf 1}+\sum_{i=1}^d w^*_i\underline{\bf x}_i$](img598.svg) |
(117) |
which is a linear combination of  and
and

We further consider the evaluation of the linear regression
result in terms of how well it fits the training data. We
first rewrite the normal equation in Eq. (115)
as:
The last equality indicate that the residual vector
 is parpendicular to each of the
is parpendicular to each of the  vectors
vectors
 :
:
 |
(119) |
We see that the residual
 based
on the optimal
based
on the optimal  represents the shortest distance
between
represents the shortest distance
between  and any point in the space spanned by
and any point in the space spanned by
 ,
i.e., any other estimate
,
i.e., any other estimate
 also
in the space but based on a non-optmal
also
in the space but based on a non-optmal
 must have a greater residual
must have a greater residual
 , i.e.,
, i.e.,  is indeed the optimal parameter based on which the sum of quared
error
is indeed the optimal parameter based on which the sum of quared
error
 of the model
of the model
 is minimized.
is minimized.
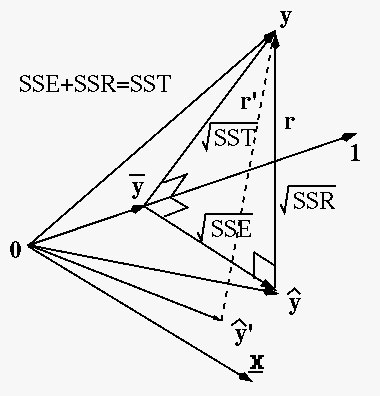
We further consider some quantitative measurement for evaluating
how well the linear regression model
 fits
the given dataset. To do so, we first derive some properties
of the model based on its output
fits
the given dataset. To do so, we first derive some properties
of the model based on its output
 :
:
based on which we also get
 |
(121) |
and
 |
(123) |
We further find the mean of

 |
(124) |
and define a vector
 .
The three vectors
.
The three vectors
 ,
,
 and
and
 are all perpendicular to vector
are all perpendicular to vector
 :
:
Based on these three vectors, we further define the following
sums of squares:
- The total sum of squares (TSS) for the total variation
in data:
 |
(126) |
- The explained sum of squares (ESS) for the variation
of data explained by the regression model:
 |
(127) |
- Residual sum of squares (RSS) for the variation of data
not explained by the data (due to noise or discrepancy between
the data and the model):
 |
(128) |
We can show that the total sum of squares is the sum of the explained
sum of squares and the residual sum of squares:
The last equality is due to the fact that the two middle terms
are both zero:
 |
(130) |
We can now measure the goodness of the model by the
coefficient of determination, denoted by  (R-squared),
defined as the percentage of variance explained by the model:
(R-squared),
defined as the percentage of variance explained by the model:
 |
(131) |
Given the total sum of squares TSS, if the model residual RSS is small,
then ESS is large, indicating most of the variation in the data can be
explained by the model, and  is large, i.e., the model is a good fit
of the data.
is large, i.e., the model is a good fit
of the data.
In the special case of 1-dimensional dataset
 , how closely the two variables
, how closely the two variables
 and
and  are correlated to each other can be measured by
correlation coefficient defined as:
are correlated to each other can be measured by
correlation coefficient defined as:
 |
(132) |
where
and
A few simple examples of different correlation coefficients can be
found here.
We can further find the linear regression model
 in
terms of the model parameters:
in
terms of the model parameters:
Based on these model parameters
 and
and
 , we get the linear regression model:
, we get the linear regression model:
 or or |
(134) |
The coefficient of determination  for the goodness of the
regression is closely related to the correlation coefficient
for the goodness of the
regression is closely related to the correlation coefficient  for correlation of the given data (but independent of the model), as
one would intuitively expect. Consider
for correlation of the given data (but independent of the model), as
one would intuitively expect. Consider
We see that if the two variables  and
and  are highly correlated
and
are highly correlated
and  is close to 1, then the error of the model is small, i.e.,
is close to 1, then the error of the model is small, i.e.,
 is small and
is small and  is large, indicating the LS
linear model fits the data well.
is large, indicating the LS
linear model fits the data well.
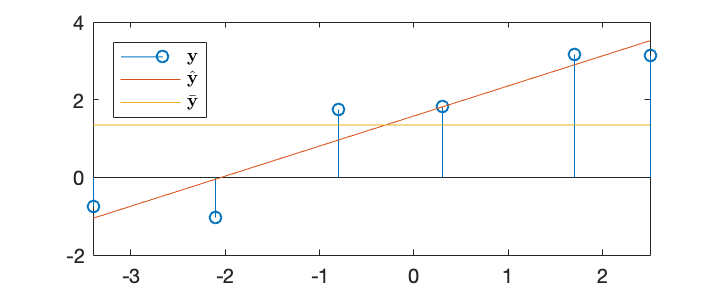
Example 1:
Find a linear regression function
 to fit the following
to fit the following
 points:
points:
Based on the data, we get
The augmented data array is:
Solving the over-constrained equation system
we get
and the linear regression model function
 ,
a straight line with intercept
,
a straight line with intercept  , slope
, slope  , and normal
direction
, and normal
direction
![$[0.78,\;-1]^T$](img675.svg) . The LS error is
. The LS error is
 . We can further get
. We can further get
![$\bar{\bf y}=[1.348,\;1.348,\;1.348,\;1.348,\;1.348,\;1.348]^T$](img677.svg) ,
,
![$\hat{\bf y}={\bf X}^T{\bf w}=[-1.054,\;-0.047,\;0.961,\;1.813,\;2.898,\;3.518]^T$](img678.svg) ,
and
We can also check that
,
and
We can also check that
Example 2:
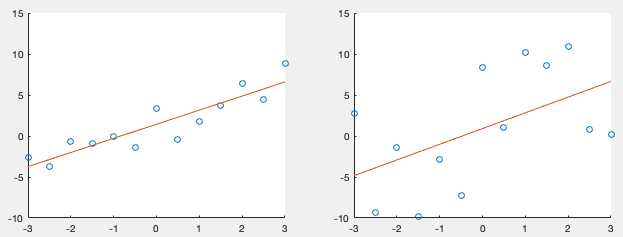
Example 3:
The figure below shows a set of  data points
data points
 fitted by a 1-D linear
regression function
fitted by a 1-D linear
regression function
 , a straight line,
with
, a straight line,
with
 . The correlation coefficient
is
. The correlation coefficient
is  , and
, and
 ,
,  .
.
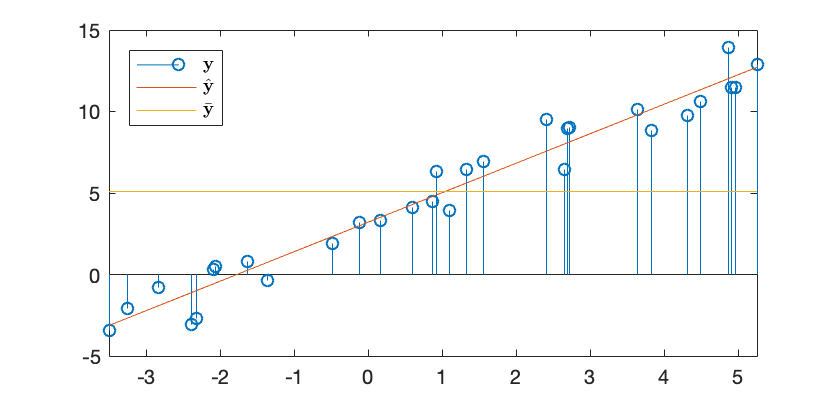
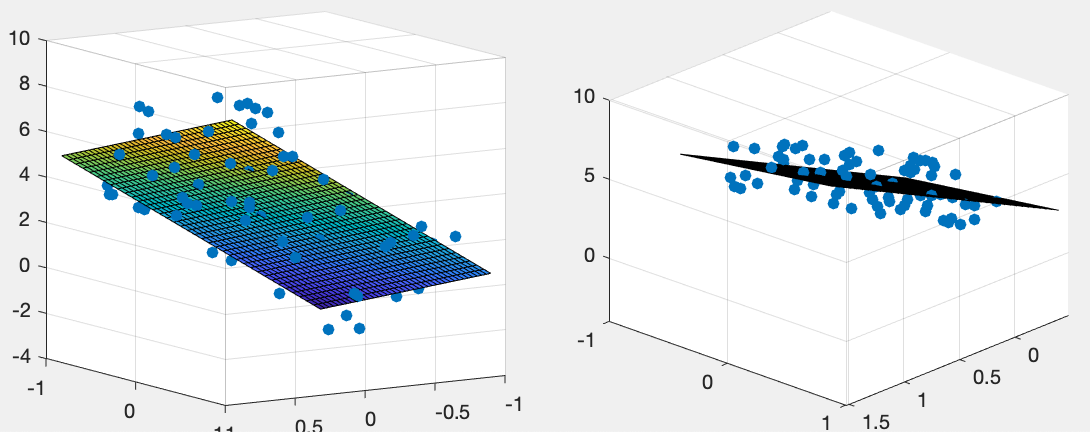
Example 4:
The figure below shows a set of  data points
data points
 fitted by a 2-D
linear regression function
fitted by a 2-D
linear regression function
 , a plane,
with
, a plane,
with
 „ and
„ and
 and
and  .
.


![${\bf x}=[x_1,\cdots,x_d]^T$](img491.svg)
![${\bf x}=[x_0=1,x_1,\cdots,x_d]^T$](img559.svg) is redefined as an
augmented
is redefined as an
augmented  dimensional vector containing
dimensional vector containing  as well as
the
as well as
the  independent variables, and
independent variables, and
![${\bf w}=[w_0=b,w_1,\cdots,w_d]^T$](img561.svg) is an argmented
is an argmented  dimensional vector containing
dimensional vector containing  as
well as the
as
well as the  weights as the parameters, to be determined
based on the given dataset.
weights as the parameters, to be determined
based on the given dataset.









![$[w_1,\cdots,w_d,\,-1]^T$](img565.svg)









![${\bf x}_n=[x_{0n}=1,\,x_{1n},\cdots,x_{dn}]^T\;(n=1,\cdots,N)$](img569.svg)
![$\displaystyle {\bf X}=\left[\begin{array}{ccc}1 &\cdots&1\\ x_{11}&\cdots&x_{1N...
...}&\cdots&x_{dN}\end{array}\right]_{(d+1)\times N}
=[{\bf x}_1,\cdots,{\bf x}_N]$](img570.svg)
![$\displaystyle {\bf X}^T=\left[\begin{array}{cccc}1 & x_{11} & \cdots & x_{d1}
\...
...imes(d+1)}
=\left[{\bf 1},\underline{\bf x}_1,\cdots,\underline{\bf x}_d\right]$](img571.svg)
![${\bf 1}=[1,\cdots,1]^T$](img572.svg) , and
, and
![$\underline{\bf x}_i=[x_{i1},\cdots,x_{iN}]^T\;\;(i=1,\cdots,d)$](img573.svg) is
an N-dimensional vectors containing the ith components of all
is
an N-dimensional vectors containing the ith components of all
 data vectors in the dataset.
data vectors in the dataset.


 . In other words,
the residual of the linear model defined as
. In other words,
the residual of the linear model defined as
 need to be zero:
This is a linear system containing
need to be zero:
This is a linear system containing  equations of
equations of  unknowns.
unknowns.





 , i.e., there are many more data
samples than the unknown parameters,
, i.e., there are many more data
samples than the unknown parameters,  is non-invertible
and
is non-invertible
and
 is over-determined linear system
without a solution, i.e, the prediction
is over-determined linear system
without a solution, i.e, the prediction
 can never match the ground truth labeling
can never match the ground truth labeling  . We need to
find an optimal solution
. We need to
find an optimal solution  that minimizes the SSE
(proportional to MSE):
that minimizes the SSE
(proportional to MSE):
 that minimizes
that minimizes
 ,
we set the gradient of
,
we set the gradient of
 to zero and get the
normal equation:
Solving for
to zero and get the
normal equation:
Solving for  , we get the optimal weight vector:
where
, we get the optimal weight vector:
where
 is the
is the
 pseudo-inverse
of the
pseudo-inverse
of the
 matrix
matrix  .
This method for estimating the regression model parameters is
called ordinary least squares (OLS).
.
This method for estimating the regression model parameters is
called ordinary least squares (OLS).


![${\bf X}_*=[{\bf x}_{1*},\cdots,{\bf x}_{M*}]$](img597.svg)
 and
and

 is parpendicular to each of the
is parpendicular to each of the  vectors
vectors
 :
We see that the residual
:
We see that the residual
 based
on the optimal
based
on the optimal  represents the shortest distance
between
represents the shortest distance
between  and any point in the space spanned by
and any point in the space spanned by
 ,
i.e., any other estimate
,
i.e., any other estimate
 also
in the space but based on a non-optmal
also
in the space but based on a non-optmal
 must have a greater residual
must have a greater residual
 , i.e.,
, i.e.,  is indeed the optimal parameter based on which the sum of quared
error
is indeed the optimal parameter based on which the sum of quared
error
 of the model
of the model
 is minimized.
is minimized.


















 .
The three vectors
.
The three vectors
 ,
,
 and
and
 are all perpendicular to vector
are all perpendicular to vector
 :
:
























 is large, i.e., the model is a good fit
of the data.
is large, i.e., the model is a good fit
of the data.









![$\displaystyle \left[\begin{array}{c}w_0\\ w_1\end{array}\right]
=({\bf X}{\bf X...
..._N\end{array}\right]
\left[\begin{array}{c}y_1\\ \vdots\\ y_N\end{array}\right]$](img652.svg)

![$\displaystyle \left[\begin{array}{ccc}N&\sum_{n=1}^Nx_n\\ \sum_{n=1}^Nx_n&\sum_...
...\left[\begin{array}{c}\bar{y}\\ \sigma_{xy}^2+\bar{x}\bar{y} \end{array}\right]$](img653.svg)

![$\displaystyle \frac{1}{\sigma_x^2}
\left[\begin{array}{ccc}\sigma_x^2+\bar{x}^2...
...sigma_{xy}^2/\sigma_x^2 \;\bar{x}\\
\sigma_{xy}^2/\sigma_x^2\end{array}\right]$](img654.svg)
 and
and
 , we get the linear regression model:
, we get the linear regression model:
 or
or






![$\displaystyle \frac{1}{N}\sum_{n=1}^N[(y_n-\bar{y})-w_1(x_n-\bar{x})]^2
=\frac{...
...um_{n=1}^N[(y_n-\bar{y})^2-2w_1(y_n-\bar{y})(x_n-\bar{x})+w_1^2(x_n-\bar{x})^2]$](img662.svg)




 and
and  are highly correlated
and
are highly correlated
and  is close to 1, then the error of the model is small, i.e.,
is close to 1, then the error of the model is small, i.e.,
 is small and
is small and  is large, indicating the LS
linear model fits the data well.
is large, indicating the LS
linear model fits the data well.




![$\displaystyle {\bf X}=\left[\begin{array}{cccccc}1&1&1&1&1&1\\
-3.4 & -2.1 & -0.8 & 0.3 & 1.7 & 2.5
\end{array}\right]
\\ $](img669.svg)
![$\displaystyle {\bf y}=\left[\begin{array}{c}-0.76\\ -1.04\\ 1.75\\ 1.82\\ 3.17\...
... 1&2.5
\end{array}\right]
\left[\begin{array}{c}w_0\\ w_1\end{array}\right]
\\ $](img670.svg)
![$\displaystyle {\bf w}={\bf X}^- {\bf y}=({\bf X}{\bf X}^T)^{-1}{\bf X}\;{\bf y}...
....15
\end{array}\right]
=\left[\begin{array}{c}1.58\\ 0.78\end{array}\right]
\\ $](img671.svg)
 ,
a straight line with intercept
,
a straight line with intercept  , slope
, slope  , and normal
direction
, and normal
direction
![$[0.78,\;-1]^T$](img675.svg) . The LS error is
. The LS error is
 . We can further get
. We can further get
![$\bar{\bf y}=[1.348,\;1.348,\;1.348,\;1.348,\;1.348,\;1.348]^T$](img677.svg) ,
,
![$\hat{\bf y}={\bf X}^T{\bf w}=[-1.054,\;-0.047,\;0.961,\;1.813,\;2.898,\;3.518]^T$](img678.svg) ,
and
,
and




















