Next: Gradient Descent Method Up: Unconstrained Optimization Previous: Nelder-Mead method
Newton's method is based on the
Taylor series expansion
of the function 

 |
 |
 |
|
 |
 |
(28) |
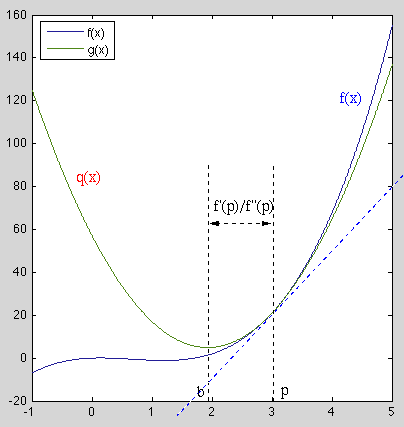
If 

 |
 |
![$\displaystyle \frac{d}{dx}q(x)=\frac{d}{dx}\left[ f(x_0)+f'(x_0)(x-x_0)
+\frac{1}{2}f''(x_0)(x-x_0)^2 \right]$](img161.svg) |
|
 |
 |
(29) |
 to get:
where
to get:
where
 is the step we need to take
to go from any initial point
is the step we need to take
to go from any initial point  to the solution
to the solution  in a
single step. Note that
in a
single step. Note that  is a minimum if
is a minimum if
 but
a maximum if
but
a maximum if
 .
.
If


 |
(31) |
 .
We see that in each step
.
We see that in each step  of the iteration, the function
of the iteration, the function
 is fitted by a quadratic functions
is fitted by a quadratic functions  and its vertex
at
and its vertex
at  is used as the updated approximated solution, at
which the function is again fitted by another quadratic function
is used as the updated approximated solution, at
which the function is again fitted by another quadratic function
 for the next iteration. Through this process the
solution can be approached as
for the next iteration. Through this process the
solution can be approached as
 .
.
We note that the iteration



Newton's method for the minimization of a single-variable
function 




 |
(32) |
 and
and  are respectively the gradient vector and
Hessian matrix of the function
are respectively the gradient vector and
Hessian matrix of the function
 at
at  :
:
 |
 |
![$\displaystyle {\bf g}_f({\bf x}_0)=\frac{d}{d{\bf x}} f({\bf x}_0)
=\left[\begi...
...x_1}\\
\vdots \\ \frac{\partial f({\bf x}_0)}{\partial x_N}\end{array}\right],$](img185.svg) |
|
 |
 |
![$\displaystyle {\bf H}_f({\bf x}_0)=\frac{d}{d{\bf x}} {\bf g}({\bf x}_0)
=\frac...
...1} &
\cdots & \frac{\partial^2 f({\bf x}_0)}{\partial x_N^2}
\end{array}\right]$](img187.svg) |
(33) |
 can be found
from any point
can be found
from any point  by setting its derivative to zero
by setting its derivative to zero
 |
 |
![$\displaystyle \frac{d}{d{\bf x}}\left[f({\bf x}_0)+{\bf g}_0^T({\bf x}-{\bf x}_0)
+\frac{1}{2}({\bf x}-{\bf x}_0)^T{\bf H}_0\,({\bf x}-{\bf x}_0)\right]$](img190.svg) |
|
 |
 |
(34) |
 |
(35) |
 is either a
minimum or maximum depends on whether the second order derivative
is either a
minimum or maximum depends on whether the second order derivative
 is greater or smaller than zero, here whether
is greater or smaller than zero, here whether
 is a minimum, maximum, or neither, depends on the
second order derivatives, the Hessiam matrix
is a minimum, maximum, or neither, depends on the
second order derivatives, the Hessiam matrix
 :
:
 is positive definite (all eigenvalues are positive),
is positive definite (all eigenvalues are positive),
 is a local minimum;
is a local minimum;
 is negative definite (all eigenvalues are negative),
is negative definite (all eigenvalues are negative),
 a local maximum;
a local maximum;
 is indefinite (has both positive and negative
eigenvalues),
is indefinite (has both positive and negative
eigenvalues),
 is a saddle point (neither minimum nor
maximum).
is a saddle point (neither minimum nor
maximum).
If

 ,
,
 ,
and the increment
,
and the increment
 is called Newton search direction. We note that the
computational complexity for each iteration is
is called Newton search direction. We note that the
computational complexity for each iteration is  due to the
inverse operation
due to the
inverse operation
 .
.
We note that the iteration above is just a generalization of






The speed of convergence of the iteration can be controlled by a
parameter 
 |
(37) |
Example:
An over-constrained nonlinear equation system



 |
(38) |
The gradient of the error function is:
 |
(39) |
 |
(40) |
 is the component
of the function's Jacobian
is the component
of the function's Jacobian
 in the mth
row and ith column.
in the mth
row and ith column.
We further find the component of the Hessian

 |
 |
![$\displaystyle \frac{\partial^2}{\partial x_i\partial x_j}\frac{1}{2}\vert\vert{...
...frac{\partial}{\partial x_j}
\left[ f_m\frac{\partial f_m}{\partial x_i}\right]$](img217.svg) |
|
 |
![$\displaystyle \sum_{m=1}^M \left[
\frac{\partial f_m}{\partial x_i}\;\frac{\par...
...f_m}{\partial x_j}
+f_m \frac{\partial^2 f_m}{\partial x_i\partial x_j} \right]$](img218.svg) |
||
 |
 |
(41) |
 .
Now the Hessian can be written as
.
Now the Hessian can be written as
 |
(42) |
 that minimizes
that minimizes
 can be found iteratively:
can be found iteratively:
 |
(43) |
![[*]](crossref.png) ) in the
previous chapter.
) in the
previous chapter.
Example:
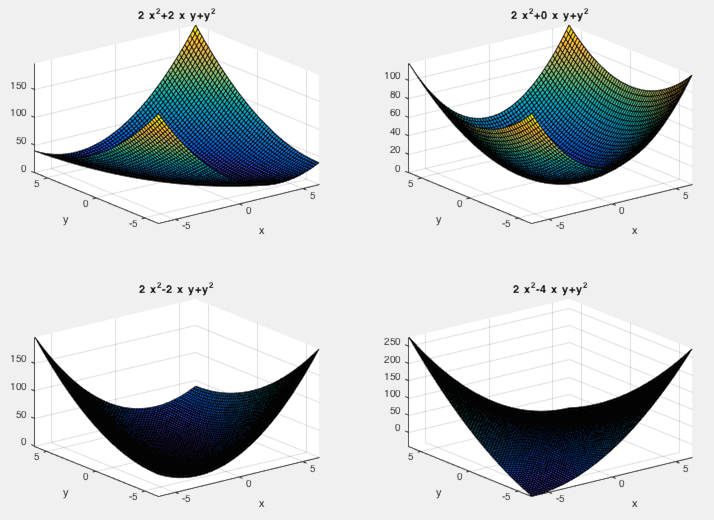
Consider the following quadratic function:
![$\displaystyle q(x,y)=\frac{1}{2} [x_1,\;x_2]
\left[\begin{array}{cc}a&b/2\\ b/2...
...\begin{array}{c}x_1\\ x_2\end{array}\right]
=\frac{1}{2}(ax_1^2+bx_1x_2+cx_2^2)$](img224.svg) |
![$\displaystyle {\bf g}=\left[\begin{array}{c}ax_1+bx_2/2\\ bx_1/2+cx_2\end{array...
...gin{array}{cc}a&b/2\\ b/2&c\end{array}\right],
\;\;\;\;\;\;\det{\bf H}=ac-b^2/4$](img225.svg) |
 ,
,  , and consider the following values of
, and consider the following values of  :
:
 ,
,
 ,
,
 ,
,
 ,
,
 is positive definite,
is positive definite,
 is the minimum.
is the minimum.
 ,
,
 ,
,
 ,
,
 ,
,
 is positive definite,
is positive definite,
 is the minimum.
is the minimum.
 ,
,
 ,
,
 ,
,
 ,
,
 is positive definite,
is positive definite,
 is the minimum.
is the minimum.
 ,
,
 ,
,
 ,
,
 ,
,
 is indefinite,
is indefinite,
 is a saddle point (minimum in one direction
but maximum in another).
is a saddle point (minimum in one direction
but maximum in another).
We can speed up the convergence by a bigger step size 


In summary, Newton's method approximates the function






Newton's method requires the Hessian matrix as well as the gradient to be available. Moreover, it is necessary calculate the inverse of the Hessian matrix in each iteration, which may be computationally expensive.
Example:
The Newton's method is applied to solving the following non-linear equation
system of 
 |
 . These equations can
be expressed in vector form as
. These equations can
be expressed in vector form as
 and solved as an
optimization problem with the objective function
and solved as an
optimization problem with the objective function
 . The iteration from an
initial guess
. The iteration from an
initial guess
 is shown below.
is shown below.
 |
(44) |
 :
:
![$\displaystyle {\bf x}^*=\left[\begin{array}{r}0.5000008539707297\\ 0.0032017070323056\\
-0.4999200212218281\end{array}\right]$](img257.svg) |
(45) |