Next: Gaussian Process Regression Up: Regression Analysis and Classification Previous: Logistic Regression and Binary
In a multiclass classification problem, an unlabeled data
point 





Any binary classifier, such as the logistic regression considered above, can be used to solve such a multiclass classification problem in either of the following two ways:
 binary classifiers
for every pair of the
binary classifiers
for every pair of the  classes based on the training set
classes based on the training set
 , then an
unlabeled sample
, then an
unlabeled sample  is classified to one of the
is classified to one of the  classes with maximum votes out of this many binary classifications.
classes with maximum votes out of this many binary classifications.
 binary problems by regrouping the
binary problems by regrouping the  classes into two classes
classes into two classes
 and
and
 , and get the
corresponding discriminant function
, and get the
corresponding discriminant function
 of the binary
problem:
of the binary
problem:
if  then then  |
(230) |
 belongs to class
belongs to class  , instead of
, instead of  containing the
rest
containing the
rest  classes. This process is repeated
classes. This process is repeated  times for all
times for all
 to get
to get
 |
(231) |
 belongs to class
belongs to class  .
.
Alternatively, a multiclass problem with 


 |
(232) |
 |
(233) |
 is the Dirac delta function which is 1 if
is the Dirac delta function which is 1 if
 , but 0 otherwise.
, but 0 otherwise.
Similar to how the logistic function is used to model the
conditional probability







![${\bf W}=[{\bf w}_1,\cdots,{\bf w}_K]$](img1079.svg)
![${\bf W}=[{\bf w}_1,\cdots,{\bf w}_K]$](img1079.svg) is composed of
is composed of
 weight vectors each associated with one of the
weight vectors each associated with one of the  classes
classes
 , to be determined in the training process
based on training set
, to be determined in the training process
based on training set  . Same as in logistic regression,
here both
. Same as in logistic regression,
here both  and
and  are augmented
are augmented  dimensional
vectors.
dimensional
vectors.
We note that the inner product










Specially, when 
 |
 |
 |
|
 |
 |
 |
(236) |
 , as the vector
between the two classes of
, as the vector
between the two classes of  and
and  , which is the normal
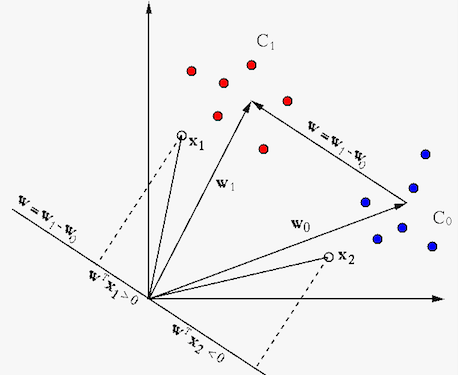
direction of a decision plane separating the two classes. Any
point
, which is the normal
direction of a decision plane separating the two classes. Any
point  of unknown class can be therefore classified into
either of the two classes depending on whether its projection
of unknown class can be therefore classified into
either of the two classes depending on whether its projection
 onto
onto  is positive or negative, i.e.,
on which side of the decision plane it is located.
is positive or negative, i.e.,
on which side of the decision plane it is located.
For mathamatical convenience, we also label each sample

![${\bf y}_n=[y_{n1},\cdots,y_{nK}]^T$](img1091.svg)









![${\bf X}=[{\bf x}_1,\cdots,{\bf x}_N]$](img498.svg)
![${\bf Y}=[{\bf y}_1,\cdots,{\bf y}_N]$](img1098.svg)
We define the probability for


 to be correctly classified
into class
to be correctly classified
into class  can be written as the
following product of
can be written as the
following product of  factors (of which
factors (of which  are equal to 1):
are equal to 1):
Our goal is to find these weight vectors in
![${\bf W}=[{\bf w}_1,\cdots,{\bf w}_K]$](img1079.svg)

 |
 |
 |
|
 |
 |
||
 |
![$\displaystyle -\sum_{n=1}^N \left[\sum_{k=1}^K y_{nk} {\bf w}_k^T{\bf x}_n
-\sum_{k=1}^K y_{nk}
\left(\log\sum_{l=1}^K e^{{\bf w}_l^T{\bf x}_n}\right)\right]$](img1109.svg) |
||
 |
![$\displaystyle -\sum_{n=1}^N \left[\sum_{k=1}^K y_{nk} {\bf w}_k^T{\bf x}_n
-\log\sum_{l=1}^K e^{{\bf w}_l^T{\bf x}_n}\right]$](img1110.svg) |
(240) |
 terms is independent of
terms is independent of  and
and
 . Also, same
as in the cae of
. Also, same
as in the cae of  , to avoid overfitting, we could further
include in this objective function extra regularization terms
, to avoid overfitting, we could further
include in this objective function extra regularization terms
 to penalize large
weights for smoother thresholding:
to penalize large
weights for smoother thresholding:
 |
(241) |
To find the optimal 



 is the residual, the difference between
the model output
is the residual, the difference between
the model output  and the binary labeling
and the binary labeling  , the ith
component of
, the ith
component of  that labels
that labels  as well as
as well as  .
.
As 

![${\bf W}=[{\bf w}_1,\cdots,{\bf w}_K]$](img1079.svg)






We stack all 






![$\displaystyle {\bf g}_J=\left[\begin{array}{c}{\bf g}_1\\
\vdots\\ {\bf g}_K\end{array}\right]$](img1132.svg) |
(243) |
 that minimize
the objective function
that minimize
the objective function
 can be found by the gradient
descent method.
can be found by the gradient
descent method.
We can also find the optimal 







 |
 |
![$\displaystyle \frac{d^2}{d{\bf w}_j d{\bf w}_i}J({\bf W})
=\frac{d}{d{\bf w}_j}...
...bf w}_j}{\bf g}_i
=\frac{d}{d{\bf w}_j}\left[{\bf Xr}_i+\lambda{\bf w}_i\right]$](img1138.svg) |
|
 |
 |
(244) |
 is the
is the
 Jacobian matrix
of
Jacobian matrix
of
 with respect to
with respect to  , of which the nth row is
the transpose of the following vector:
, of which the nth row is
the transpose of the following vector:
 |
 |
 |
|
 |
 |
(245) |
 . Now the Jacobian can be written as
. Now the Jacobian can be written as
![$\displaystyle {\bf J}_{ij}
=\left[\begin{array}{c}
dr_{i1}/d{\bf w}_j\\ \vdots ...
...array}{c}{\bf x}_1^T\\ \vdots\\ {\bf x}_N^T\end{array}\right]
={\bf Z}{\bf X}^T$](img1146.svg) |
(246) |
 is an
is an  diagonal
matrix. Substituting
diagonal
matrix. Substituting
 back into the expression
for
back into the expression
for
 , we get:
, we get:
 |
(247) |
Here










![${\bf W}=[{\bf w}_1,\cdots,{\bf w}_K]$](img1079.svg)
![$\displaystyle {\bf H}_J=\left[\begin{array}{ccc}
{\bf H}_{11} & \cdots &{\bf H}...
...dots & \ddots & \vdots\\ {\bf H}_{K1} & \cdots &{\bf H}_{KK}
\end{array}\right]$](img1155.svg) |
(248) |
 iteratively by
the Newton-Raphson method based on both
iteratively by
the Newton-Raphson method based on both  and
and  :
:
![$\displaystyle \left[\begin{array}{c}{\bf w}_1\\ \vdots\\ {\bf w}_K\end{array}\r...
...{-1}_n
\left[\begin{array}{c}{\bf g}_1\\ \vdots\\ {\bf g}_K\end{array}\right]_n$](img1157.svg) |
(249) |
Once
![${\bf W}=[{\bf w}_1,\cdots,{\bf w}_K]$](img1079.svg)


if then then |
(250) |
Whether we should use softmax regression or 



Below is a Matlab function for estimating the 
![${\bf W}=[{\bf w}_1,\cdots,{\bf w}_K]$](img1079.svg)


function W=softmaxRegression(X,y,lambda)
[d N]=size(X);
K=length(unique(y)); % number of classes
X=[ones(1,N); X]; % augmented data points
d=d+1;
Y=zeros(K,N);
for n=1:N
Y(y(n),n)=1; % generate binary labeling Y
end
W=zeros(d*K,1); % initial guess of K weight vectors
I=eye(K);
s=zeros(K,N);
phi=zeros(K,N); % softmax functions
gi=zeros(d,1); % ith gradient
Hij=zeros(d,d); % ij-th Hebbian
er=9;
tol=10^(-6);
it=0;
while er>tol
it=it+1;
W2=reshape(W,d,K); % weight vectors in d x K 2-D array
g=[]; % total gradient vector
for i=1:K
for n=1:N
xn=X(:,n); % get the nth sample
t=0;
for k=1:K
wk=W2(:,k); % get the kth weight vector
s(k,n)=exp(wk'*xn);
t=t+s(k,n);
end
phi(i,n)=s(i,n)/t; % softmax function
end
gi=X*(phi(i,:)-Y(i,:))'+lambda*W2(:,i); % ith gradient
g=[g; gi]; % stack all gradients into a long gradient vector
end
H=[]; % total Hessian
z=zeros(N,1);
for i=1:K % for the ith block row
Hi=[];
for j=1:K % for the jth block in ith row
for n=1:N
z(n)=phi(i,n)*((i==j)-phi(j,n));
end
Hij=X*diag(z)*X';
Hi=[Hi Hij]; % append jth block
end
H=[H; Hi]; % append ith blow row
end
H=H+lambda*eye(d*K); % include regulation term
W=W-inv(H)*g; % update W by Newton's method
er=norm(g);
end
W=reshape(W,d,K); % reshape weight vector into d x K array
end
Here is the function for the classification of the unlabeled
data samples in matrix 
![${\bf W}=[{\bf w}_1,\cdots,{\bf w}_K]$](img1079.svg)
function yhat=softmaxClassify(W,X)
[d N]=size(X); % dataset to be classified
[d K]=size(W); % model parameters
X=[ones(1,N); X]; % augmented data points
yhat=zeros(N,1);
for n=1:N % for each of the N samples
xn=X(:,n); % nth sample point
t=0;
for k=1:K
wk=W(:,k); % kth weight vector
s(k)=exp(wk'*xn);
t=t+s(k);
end
pmax=0;
for k=1:K
p=s(k)/t; % probability based on softmax function
if p>pmax
kmax=k; pmax=p;
end
end
yhat(n)=kmax; % predicted class labeling
end
end