Next: Solving Linear Equation Systems Up: ch2 Previous: ch2
 is to
find the zero or root
is to
find the zero or root  of the function
of the function  , at
which
, at
which  . Graphically, the root of a function
. Graphically, the root of a function  can
be found in the x-y plane as the intersection of the curve
can
be found in the x-y plane as the intersection of the curve  with the horizontal axis for
with the horizontal axis for  , if they do intersect, i.e., if
the root exists. A function may have zero root such as
, if they do intersect, i.e., if
the root exists. A function may have zero root such as
 ,
a unique root such as
,
a unique root such as  for
for  , or multiple roots such as
, or multiple roots such as
 for
for
 .
.
 and
and
 are the points
are the points  in the x-y plane
at which both functions are zero. Graphically, a function
in the x-y plane
at which both functions are zero. Graphically, a function  can
be represented as a surface in a 3-D space with the third (vertical)
dimension for the value of the function
can
be represented as a surface in a 3-D space with the third (vertical)
dimension for the value of the function  at the point at
at the point at
 . The roots of this function, if exist, are the intersection
of the surface and the x-y plane, a curve on the x-y plane. On one
side of the curve
. The roots of this function, if exist, are the intersection
of the surface and the x-y plane, a curve on the x-y plane. On one
side of the curve
 , while on the other side
, while on the other side
 .
If
.
If  has no solution, then the intersection does not exist.
The roots for both
has no solution, then the intersection does not exist.
The roots for both  and
and  are the points on the
intersections of the two curves representing the individual roots of
the two function, if they do intersect. Again there may be zero, one,
or multiple such points.
are the points on the
intersections of the two curves representing the individual roots of
the two function, if they do intersect. Again there may be zero, one,
or multiple such points.
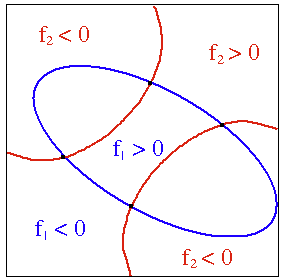
 , we need to find all points
, we need to find all points
 in an N-D vector space at which all
in an N-D vector space at which all  equations
are zero. This problem can be viewed in an
equations
are zero. This problem can be viewed in an  dimensional space, in
which the value of each function
dimensional space, in
which the value of each function
 is represented in
the (N+1)th dimension as a function of the N-D points
is represented in
the (N+1)th dimension as a function of the N-D points
 in the space formed by the remaining dimensions, i.e., a hyper-surface
in the N+1 dimensional space. Moreover, the roots of the equation
in the space formed by the remaining dimensions, i.e., a hyper-surface
in the N+1 dimensional space. Moreover, the roots of the equation
 is an N-D hyper-surface, which is the intersection
of the hyper-surface in the (N+1)th dimension with the N-D space
representing the
is an N-D hyper-surface, which is the intersection
of the hyper-surface in the (N+1)th dimension with the N-D space
representing the  variables. The solutions of all the equation system
are therefore the intersections of all
variables. The solutions of all the equation system
are therefore the intersections of all  such hyper-surfaces.
such hyper-surfaces.
Example: Consider a simultaneous equation system:
 |
The first function 





 , there are two roots
, there are two roots  and
and  ;
;
 , there is only one root
, there is only one root  ;
;
 , the two curves do not intersect, i.e., there are no roots.
, the two curves do not intersect, i.e., there are no roots.