To solve equation  , we first consider the Taylor series
expansion of
, we first consider the Taylor series
expansion of  at any point
at any point  :
:
 |
(66) |
If  is linear, i.e., its slope
is linear, i.e., its slope  is a constant for any
is a constant for any
 , then the second and higher order terms are all zero, and the
equation
, then the second and higher order terms are all zero, and the
equation  becomes
becomes
 |
(67) |
Solving this equation we get the root  at which
at which  :
:
 |
(68) |
where
 is the step we need to take to
go from the initial point
is the step we need to take to
go from the initial point  to the root
to the root  :
:
 |
(69) |
If  is nonlinear, the sum of the first two terms of the Taylor
expansion is only an approximation of
is nonlinear, the sum of the first two terms of the Taylor
expansion is only an approximation of  , and the resulting
, and the resulting  found above can be treated as an approximation of the root, which can
be improved iteratively to move from the initial point
found above can be treated as an approximation of the root, which can
be improved iteratively to move from the initial point  towards
the root, as illustrated in the figure below:
towards
the root, as illustrated in the figure below:
 |
(70) |
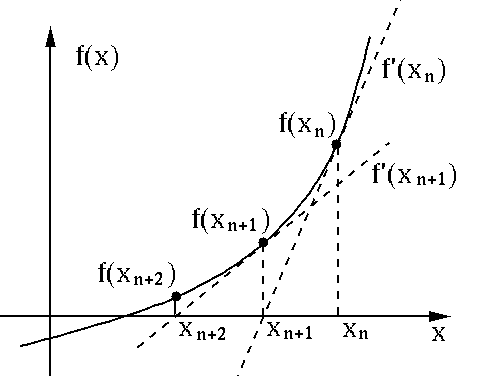
The Newton-Raphson method can be considered as the fixed point
iteration
 based on
based on
 |
(71) |
The root  at which
at which  is also the fixed point of
is also the fixed point of  ,
i.e.,
,
i.e.,
 . For the iteration to converge,
. For the iteration to converge,  needs to be
a contraction with
needs to be
a contraction with  . Consider
. Consider
 |
(72) |
We make the following comments:
The order of convergence of the Newton-Raphson iteration can be found
based on the Taylor expansion of  at the neighborhood of the root
at the neighborhood of the root
 :
:
 |
(74) |
where
 is the error at the nth step.
Substituting the Newton-Raphson's iteration
is the error at the nth step.
Substituting the Newton-Raphson's iteration
 i.e. i.e. |
(75) |
into the equation above, we get
i.e.
 |
(77) |
When
 all the higher order terms disappear, and the
above can be written as
all the higher order terms disappear, and the
above can be written as
 |
(78) |
Alternatively, we can get the Taylor expansion in terms of  :
:
 |
(79) |
Subtracting
 from both sides we get:
from both sides we get:
 |
(80) |
Now we find  and
and  :
:
 |
(81) |
and
Evaluating these at  at which
at which  , and substituting them
back into the expression for
, and substituting them
back into the expression for  above, the linear term is zero as
above, the linear term is zero as
 , i.e., the convergence is quadratic, and we get the same
result:
, i.e., the convergence is quadratic, and we get the same
result:
 |
(83) |
We see that, if
 , then the order of convergence of
the Newton-Raphson method is
, then the order of convergence of
the Newton-Raphson method is  , and the rate of convergence is
, and the rate of convergence is
 . However, if
. However, if  , the convergence
is linear rather than quadratic, as shown in the example below.
, the convergence
is linear rather than quadratic, as shown in the example below.
Example: Consider solving the equation
 |
(84) |
which has a repeated root  as well as a single root
as well as a single root  . We
have
. We
have
 |
(85) |
Note that at the root  we have
we have
 . We further
find:
. We further
find:
 |
(86) |
and
We therefore have
 |
(87) |
We see the iteration converges quadratically to the single root  ,
but only linearly to the repeated root
,
but only linearly to the repeated root  .
.
We consider in general a function with a repeated root at  of
multiplicity
of
multiplicity  :
:
 |
(88) |
its derivative is
![$\displaystyle f'(x)=k(x-a)^{k-1}h(x)+(x-a)^kh'(x)=(x-a)^{k-1}[kh(x)+(x-a)h'(x)]$](img399.svg) |
(89) |
As  , the convergence of the Newton-Raphson method to
, the convergence of the Newton-Raphson method to  is
linear, rather than quadratic.
is
linear, rather than quadratic.
In such case, we can accelerate the iteration by using a step size
 :
:
 |
(90) |
and
 |
(91) |
Now we show that this  is zero at the repeated root
is zero at the repeated root  ,
therefore the convergence to this root is still quadratic.
,
therefore the convergence to this root is still quadratic.
We substitute
 ,
,
![$f'(x)=k(x-a)^{k-1}[kh+(x-a)h']$](img405.svg) , and
, and
into the expression for  above to get (after some algebra):
above to get (after some algebra):
At  , we get
, we get
 |
(94) |
i.e., the convergence to the repeated root at  is no longer
linear but quadratic.
is no longer
linear but quadratic.
The difficulty, however, is that the multiplicity  of a root is
unknown ahead of time. If
of a root is
unknown ahead of time. If  is used blindly some root may be
skipped, and the iteration may oscillate around the real root.
is used blindly some root may be
skipped, and the iteration may oscillate around the real root.
Example: Consider solving
 ,
with a double root
,
with a double root  and a single root
and a single root  . In the following,
we compare the performance of both
. In the following,
we compare the performance of both
 and
and
 .
.
- First use an initial guess
 .
.
- When
 is used, the convergence is linear around the
double root
is used, the convergence is linear around the
double root  . It takes 16 iterations to get
. It takes 16 iterations to get
 with
with
 :
:
- When
 is used, the convergence is quadratic around
the double root
is used, the convergence is quadratic around
the double root  . It takes only 3 iterations to get
. It takes only 3 iterations to get
 with
with
 :
:
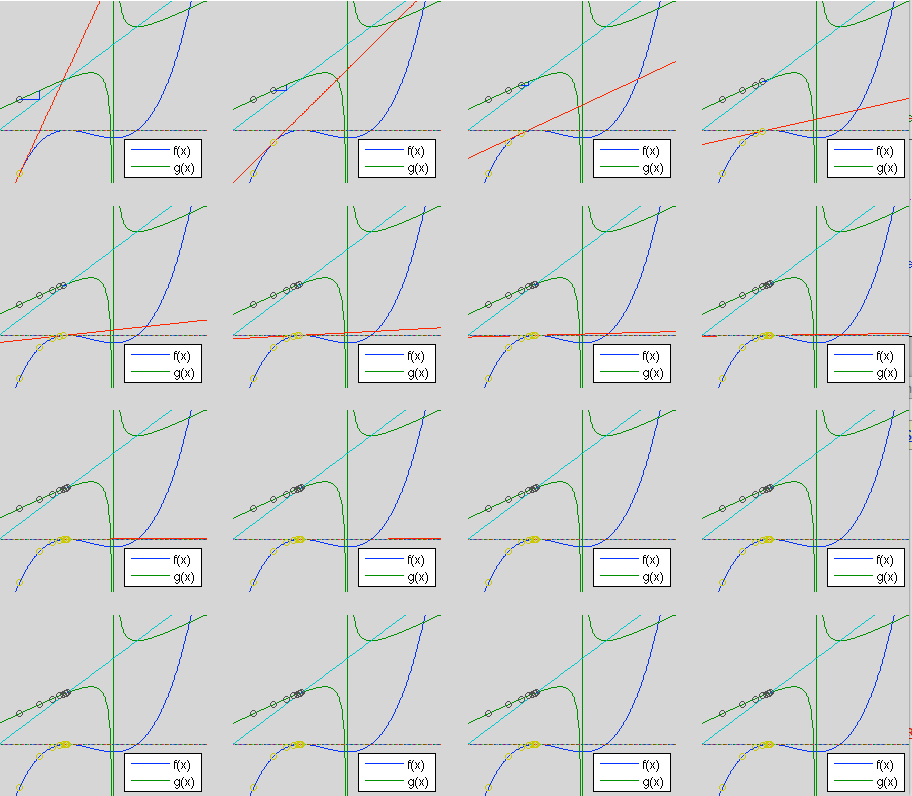
- Next use a different initial guess
 .
.
- If
 is used, it takes 7 iterations to get
is used, it takes 7 iterations to get  with
with
 , the convergence is quadratic.
, the convergence is quadratic.
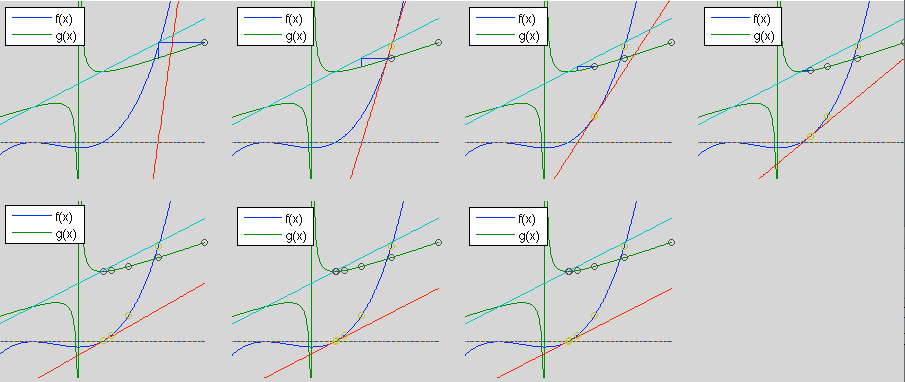
- If
 is used, oscillation happens as shown in the
figure below. However, if a better initial guess
is used, oscillation happens as shown in the
figure below. However, if a better initial guess  is used instead of
is used instead of  , it takes only one step to get
, it takes only one step to get
 with
with
 , the convergence is significantly
accelerated.
, the convergence is significantly
accelerated.





 is linear, i.e., its slope
is linear, i.e., its slope  is a constant for any
is a constant for any
 , then the second and higher order terms are all zero, and the
equation
, then the second and higher order terms are all zero, and the
equation  becomes
becomes

 at which
at which  :
:

 is the step we need to take to
go from the initial point
is the step we need to take to
go from the initial point  to the root
to the root  :
:








 at which
at which  is also the fixed point of
is also the fixed point of  ,
i.e.,
,
i.e.,
 . For the iteration to converge,
. For the iteration to converge,  needs to be
a contraction with
needs to be
a contraction with  . Consider
. Consider

 where
where  , if
, if
 , then
, then
 , i.e.,
, i.e.,  is a contraction and the iteration
is a contraction and the iteration
 converges quadratically when
converges quadratically when  is close to
is close to  .
.
 (the tangent is horizontal), the iteration cannot
proceed, but we can modify
(the tangent is horizontal), the iteration cannot
proceed, but we can modify  by adding a small value
by adding a small value  to
to  so that
so that
 .
.
 ) to infinity (e.g.,
) to infinity (e.g.,
 ). One can try different
initial guesses in the range of interest to see if different roots can
be found.
). One can try different
initial guesses in the range of interest to see if different roots can
be found.
 can be used to control the step size
of the iteration:
can be used to control the step size
of the iteration:

 , the iteration is de-accelerated. Although the
convergence becomes slower, this may be desirable if the function
, the iteration is de-accelerated. Although the
convergence becomes slower, this may be desirable if the function
 is not smooth with many local variations.
is not smooth with many local variations.
 , the iteration is accelerated. The convergence
may or may not be accelerated. Due to the greater step size, the
root may be skipped and missed. Sometimes the convergence may
become significantly slowed or even oscillate around the true
root, such as the example shown in the figure below with
, the iteration is accelerated. The convergence
may or may not be accelerated. Due to the greater step size, the
root may be skipped and missed. Sometimes the convergence may
become significantly slowed or even oscillate around the true
root, such as the example shown in the figure below with  .
.
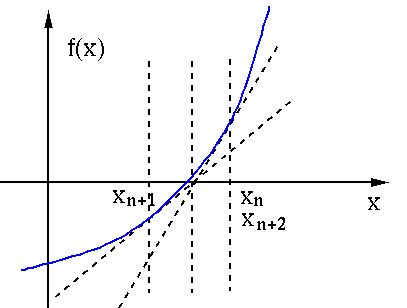



 is the error at the nth step.
Substituting the Newton-Raphson's iteration
is the error at the nth step.
Substituting the Newton-Raphson's iteration
 i.e.
i.e.





 all the higher order terms disappear, and the
above can be written as
all the higher order terms disappear, and the
above can be written as

 :
:

 from both sides we get:
from both sides we get:

 and
and  :
:






 at which
at which  , and substituting them
back into the expression for
, and substituting them
back into the expression for  above, the linear term is zero as
above, the linear term is zero as
 , i.e., the convergence is quadratic, and we get the same
result:
, i.e., the convergence is quadratic, and we get the same
result:






 as well as a single root
as well as a single root  . We
have
. We
have

 we have
we have
 . We further
find:
. We further
find:







 ,
but only linearly to the repeated root
,
but only linearly to the repeated root  .
.



![$\displaystyle f'(x)=k(x-a)^{k-1}h(x)+(x-a)^kh'(x)=(x-a)^{k-1}[kh(x)+(x-a)h'(x)]$](img399.svg)
 , the convergence of the Newton-Raphson method to
, the convergence of the Newton-Raphson method to  is
linear, rather than quadratic.
is
linear, rather than quadratic.



 is zero at the repeated root
is zero at the repeated root  ,
therefore the convergence to this root is still quadratic.
,
therefore the convergence to this root is still quadratic.

![$f'(x)=k(x-a)^{k-1}[kh+(x-a)h']$](img405.svg)
![$\displaystyle f''(x)=[(x-a)^{k-1}[kh+(x-a)h']]'$](img406.svg)

![$\displaystyle 1-k+k\,(k-1)(x-a)^{k-2}[kh+(x-a)h']$](img407.svg)
![$\displaystyle +(x-a)^{k-1}[(k+1)h'+(x-a)h'']$](img408.svg)
 above to get (after some algebra):
above to get (after some algebra):





 , we get
, we get

 is no longer
linear but quadratic.
is no longer
linear but quadratic.







 .
.
 is used, the convergence is linear around the
double root
is used, the convergence is linear around the
double root  . It takes 16 iterations to get
. It takes 16 iterations to get
 with
with
 :
:

 is used, the convergence is quadratic around
the double root
is used, the convergence is quadratic around
the double root  . It takes only 3 iterations to get
. It takes only 3 iterations to get
 with
with
 :
:


 .
.
 is used, it takes 7 iterations to get
is used, it takes 7 iterations to get  with
with
 , the convergence is quadratic.
, the convergence is quadratic.


 is used, oscillation happens as shown in the
figure below. However, if a better initial guess
is used, oscillation happens as shown in the
figure below. However, if a better initial guess  is used instead of
is used instead of  , it takes only one step to get
, it takes only one step to get
 with
with
 , the convergence is significantly
accelerated.
, the convergence is significantly
accelerated.

