To answer the question why the iterative method for solving nonlinear
equations works in some cases but fails in others, we need to understand
the theory behind the method, the fixed point of a contraction
function. If a single variable function  satisfies
satisfies
 |
(36) |
it is Lipschitz continuous, and  is a Lipschitz constant.
Specially, if
is a Lipschitz constant.
Specially, if  , then
, then  is a non-expansive function, if
is a non-expansive function, if
 , then
, then  is a contraction function or simply a
contraction. These concepts can be generated to functions of
multivariables
is a contraction function or simply a
contraction. These concepts can be generated to functions of
multivariables
![${\bf x}=[x_1,\cdots,x_N]^T\in \mathbb{R}^N$](img196.svg) (a point in
an N-D metric space
(a point in
an N-D metric space  ):
):
 |
(37) |
which can also be expressed in vector form:
![$\displaystyle {\bf g}({\bf x})=[g_1({\bf x}),\cdots,g_N({\bf x})]^T$](img199.svg) |
(38) |
Definition: In a metric space  with certain distance
with certain distance
 defined between any two points
defined between any two points
 , a function
, a function
 is a contraction if
is a contraction if
 |
(39) |
The smallest  value that satisfies the above is called the
(best) Lipschitz constant.
value that satisfies the above is called the
(best) Lipschitz constant.
In the following, we will use the
p-norm
of the vector
 defined below as the distance
measurement:
defined below as the distance
measurement:
 |
(40) |
where  , e.g.,
, e.g.,
 . Also, for conveninece, we can
drop
. Also, for conveninece, we can
drop  so that
so that
 .
.
Intuitively, a contraction reduces the distance between points in the
space, i.e., it brings them closer together. A function
 may not be a contraction through out its entire domain, but it can be
a contraction in the neighborhood of a certain point
may not be a contraction through out its entire domain, but it can be
a contraction in the neighborhood of a certain point
 ,
in which any
,
in which any  is sufficiently close to
is sufficiently close to  so that
so that
 when when  |
(41) |
Definition:
A fixed point  of a function
of a function
 is a
point in its domain that is mapped to itself:
is a
point in its domain that is mapped to itself:
 |
(42) |
We immediately have
 |
(43) |
A fixed point  is an attractive fixed point if any
point
is an attractive fixed point if any
point  in its neighborhood converges to
in its neighborhood converges to  , i.e.,
, i.e.,
 .
.
Fixed Point Theorem : Let
 be a contraction
function satisfying
be a contraction
function satisfying
 |
(44) |
then there exists a unique fixed point
 ,
which can be found by an iteration from an arbitrary initial point
,
which can be found by an iteration from an arbitrary initial point
 :
:
 |
(45) |
Proof
QED
Theorem:
Let
 be a fixed point of a differentiable
function
be a fixed point of a differentiable
function
 , i.e,
, i.e,
 exists for
any
exists for
any
 . If the norm of the Jacobian matrix is smaller than 1,
. If the norm of the Jacobian matrix is smaller than 1,
 , then
, then
 is a contraction
at
is a contraction
at  .
.
The Jacobian matrix of
 is defined as
is defined as
![$\displaystyle {\bf g}'({\bf x})={\bf J}_{\bf g}({\bf x})=\left[\begin{array}{cc...
... g_N}{\partial x_1}&\cdots&\frac{\partial g_N}{\partial x_N}
\end{array}\right]$](img234.svg) |
(49) |
Proof: Consider the Taylor expansion
of the function
 in the neighborhood of
in the neighborhood of  :
:
 |
(50) |
where
 is the remainder composed of second and higher
order terms of
is the remainder composed of second and higher
order terms of
 . Subtracting
. Subtracting
 and taking any p-norm on both sides, we get
and taking any p-norm on both sides, we get
 |
(51) |
When
 , the second and higher order terms
of
, the second and higher order terms
of
 disappear and
disappear and
 , we
have
, we
have
 |
(52) |
The inequality is due to the
Cauchy-Schwarz inequality.
if
 , the function
, the function
 is a contraction at
is a contraction at  .
.
QED
In particular, for a single-variable function in an  dimensional
space, we have
dimensional
space, we have
 |
(53) |
and
 |
(54) |
If  , then
, then  is a contraction at
is a contraction at  .
.
Now we understand why in the examples of the previous section the
iteration leads to convergence in some cases but divergence in other
cases: if  , the iteration will converge to the root
, the iteration will converge to the root  of
of  , but if
, but if  , it never will never converge.
, it never will never converge.
The iterative process
 for finding the fixed point
of a single-variable function
for finding the fixed point
of a single-variable function  can be shown graphically as
the intersections of the function
can be shown graphically as
the intersections of the function  and the identity function
and the identity function
 , as shown below. The iteration converges in the first two cases
as
, as shown below. The iteration converges in the first two cases
as  , but it diverges in the last two cases as
, but it diverges in the last two cases as  .
.
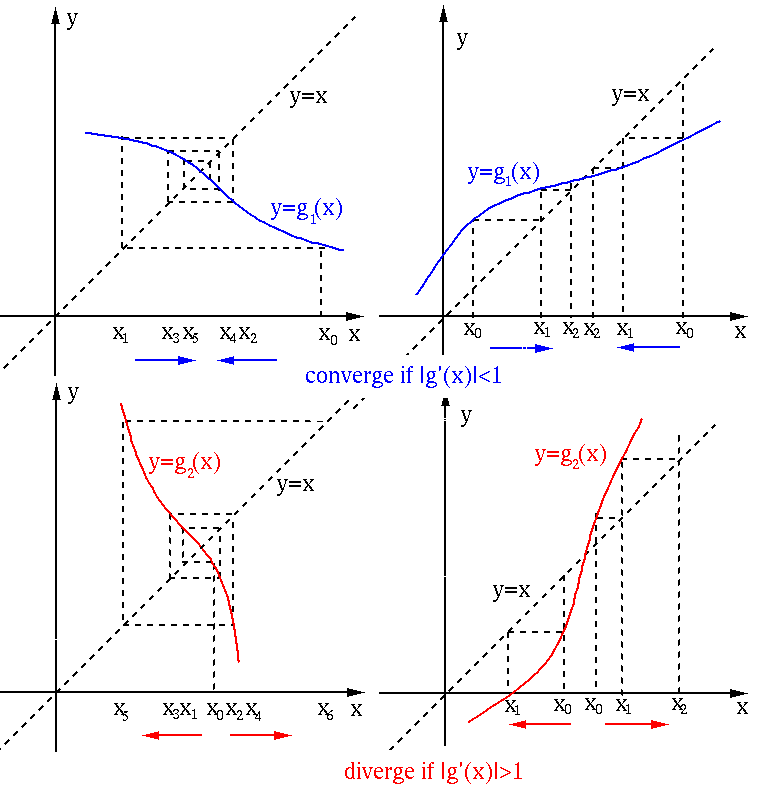
We next find the
order of convergence
of the fixed point iteration. Consider
 |
(55) |
We see that in general the fixed point iteration converges linearly.
However, if the iteration function  has zero derivative at the
fixed point
has zero derivative at the
fixed point  , we have
, we have
 |
(56) |
and the iteration converges quadratically:
 constant constant |
(57) |
Moreover, if
 , then the iteration converges cubically.
, then the iteration converges cubically.
Consider a specific iteration function in the form of
 , which is equivalent to
, which is equivalent to  , as if
, as if  is the root of
is the root of  satisfying
satisfying  , it also satisfies
, it also satisfies
 , which is indeed a fixed point of
, which is indeed a fixed point of  . The derivative
of this function is
. The derivative
of this function is
 |
(58) |
If
 , then we can define
, then we can define
 so that then
so that then
 , then the convergence becomes quadratic.
This is actually the Newton-Raphson method, to be discussed later.
, then the convergence becomes quadratic.
This is actually the Newton-Raphson method, to be discussed later.
Example 1
Find the solution of the following equation:
This equation can converted into an equivalent form of  in two
different ways:
in two
different ways:
![$\displaystyle g_1(x)=x=\sqrt[3]{x+2},\;\;\;\;\;\;\;$](img262.svg) and and |
|
In the figure below, the two functions  (left) and
(left) and  (right) together with
(right) together with  and the identity function are plotted:
and the identity function are plotted:
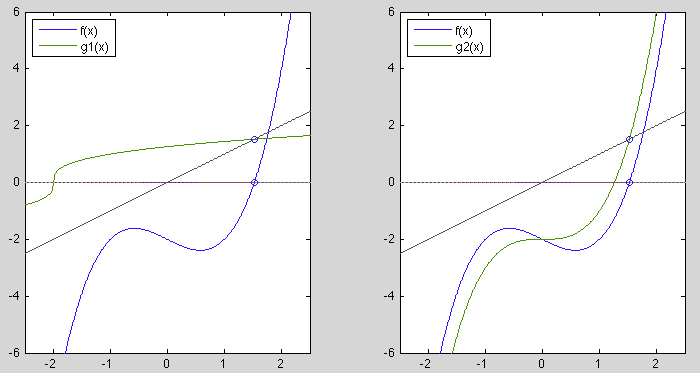
The iteration based on  converges to the solution
converges to the solution
 for any initial guess
for any initial guess
 , as
, as  is a contraction.
However, the iteration based on
is a contraction.
However, the iteration based on  does not converge to
does not converge to  as it
is not a contraction in the neighborhood of
as it
is not a contraction in the neighborhood of  . In fact, the iteration
will diverge towards either
. In fact, the iteration
will diverge towards either  if
if  or
or  if
if  .
.
Example 2
To solve the following equation
we first convert it into the form of  in two different ways:
in two different ways:
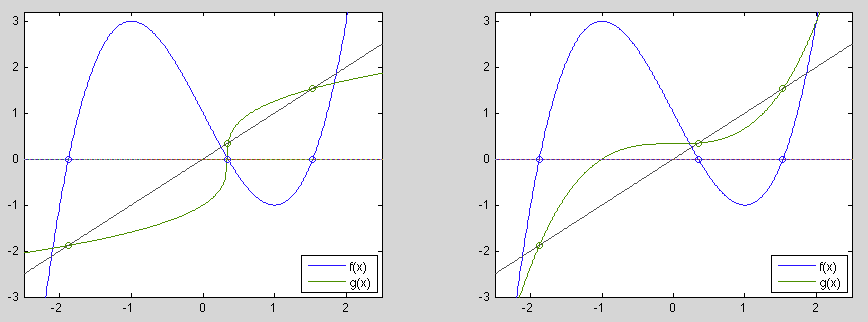
As can be seen in the plots, this equation has three solutions,
of which  and
and  can be obtained by the iteration based on
can be obtained by the iteration based on
 and
and  can be obtained by the iteration based on
can be obtained by the iteration based on  .
But neither of them can find all three roots.
.
But neither of them can find all three roots.
- As shown in the plot on the left,
 for all
for all
 except in the neighborhood of
except in the neighborhood of
 ,
i.e.,
,
i.e.,  is a contraction mapping everywhere except around
is a contraction mapping everywhere except around
 . Therefore the iteration starting from any initial guess
. Therefore the iteration starting from any initial guess
 will converge to either
will converge to either
 if
if  , or
, or
 if
if  .
However, as
.
However, as  is not a contraction mapping around
is not a contraction mapping around  ,
the iteration will never converge to
,
the iteration will never converge to  .
.
- As shown in the plot on the right,
 for all
for all
 except in the neighborhood of
except in the neighborhood of  , i.e.,
, i.e.,
 is not a contraction mapping around either
is not a contraction mapping around either  or
or  .
Therefore the iteration based on
.
Therefore the iteration based on  will not converge to
either
will not converge to
either  or
or  , but it may converge to
, but it may converge to  , if the initial
guess
, if the initial
guess  is in the range
is in the range
 . However, if
. However, if  is outside
this range the iteration will diverge toward either
is outside
this range the iteration will diverge toward either  if
if
 of
of  if
if  .
.
Example 3
This equation can be converted into the form  in different ways:
in different ways:
Example 4
-
The iteration from any initial guess  will converge to
will converge to
 .
.
-
Around
 ,
,
 , the iteration does not converge.
, the iteration does not converge.
-
Example 5
Consider a 3-variable linear vector function
 of arguments
of arguments
![${\bf x}=[x,\;y,\;z]^T$](img306.svg) :
:
from which the g-function can be obtained:
The Jacobian
 of this linear system is a constant
matrix
of this linear system is a constant
matrix
with the induced p=2 norm (maximum singular value)
 .
Consequently, the iteration
.
Consequently, the iteration
 converges
from an initial guess
converges
from an initial guess
![${\bf x}_0=[1,\,1,\,1]^T$](img312.svg) to the solution
to the solution
![${\bf x}=[1,\,2,\,3]^T$](img313.svg) .
.
Alternatively, the g-function can also be obtained as
The Jacobian is
with the induced p=2 norm
 . The iteration does not
converge.
. The iteration does not
converge.
Example 6
Consider a 3-variable nonlinear function
 of arguments
of arguments
![${\bf x}=[x,\;y,\;z]^T$](img306.svg) :
:
The g-function can be obtained as
With
![${\bf x}_0=[0,\;0,\;0]^T$](img319.svg) and after
and after  iterations
iterations
 converges to
converges to
![${\bf x}_n=[1.098933,\;0.367621,\;0.144932]^T$](img321.svg) , with error
, with error
 . However, the iteration may
not converge from other possible initial guesses.
. However, the iteration may
not converge from other possible initial guesses.
By Aitken's method, the iteration
 can be accelerated
based on two consecutive points
can be accelerated
based on two consecutive points  and
and  , as shown in the
figure below.
, as shown in the
figure below.
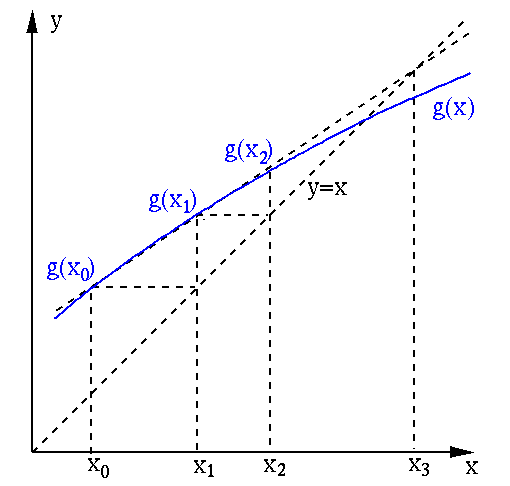
The secant line of  that goes through the two points
that goes through the two points
 and
and
 is represented by
the equation in terms of its slope:
is represented by
the equation in terms of its slope:
 |
(59) |
Solving for  , we get
, we get
 |
(60) |
To accelerate, instead of moving from  to
to  , we move to the point
, we move to the point
 at which this secant line intersects with the identity function
at which this secant line intersects with the identity function  .
We can therefore replace
.
We can therefore replace  in the equation above by
in the equation above by  and solve the
resulting equation
and solve the
resulting equation
 |
(61) |
to get
 |
(62) |
where
 and
and
 are respectively the first and second
order differences defined below:
are respectively the first and second
order differences defined below:
 |
(63) |
 |
(64) |
This result can then be converted into an iterative process
 |
(65) |
Given  , we skip
, we skip
 and
and
 but directly
move to
but directly
move to  computed based on
computed based on  and
and  , thereby making
a greater step towards the solution.
, thereby making
a greater step towards the solution.
Example Solve
 . Construct
. Construct
 .
It takes 18 iterations for the regular fixed point algorithm with
initial guess
.
It takes 18 iterations for the regular fixed point algorithm with
initial guess  , to get
, to get
 that satisfies
that satisfies
 , but it only three iterations for Aitken's method
to converge to the same result:
, but it only three iterations for Aitken's method
to converge to the same result:


 is a Lipschitz constant.
Specially, if
is a Lipschitz constant.
Specially, if  , then
, then  is a non-expansive function, if
is a non-expansive function, if
 , then
, then  is a contraction function or simply a
contraction. These concepts can be generated to functions of
multivariables
is a contraction function or simply a
contraction. These concepts can be generated to functions of
multivariables
![${\bf x}=[x_1,\cdots,x_N]^T\in \mathbb{R}^N$](img196.svg) (a point in
an N-D metric space
(a point in
an N-D metric space  ):
):

![$\displaystyle {\bf g}({\bf x})=[g_1({\bf x}),\cdots,g_N({\bf x})]^T$](img199.svg)





 value that satisfies the above is called the
(best) Lipschitz constant.
value that satisfies the above is called the
(best) Lipschitz constant.


 , e.g.,
, e.g.,
 . Also, for conveninece, we can
drop
. Also, for conveninece, we can
drop  so that
so that
 .
.




 when
when 




 is an attractive fixed point if any
point
is an attractive fixed point if any
point  in its neighborhood converges to
in its neighborhood converges to  , i.e.,
, i.e.,
 .
.


 ,
which can be found by an iteration from an arbitrary initial point
,
which can be found by an iteration from an arbitrary initial point
 :
:

 is a contraction, we have
is a contraction, we have

 , we have
, we have
 .
This is a Cauchy sequence
that converges to some point
.
This is a Cauchy sequence
that converges to some point
 also in the space.
We further have
also in the space.
We further have

 is a fixed point.
is a fixed point.
 and
and
 be two fixed points of
be two fixed points of
 , then we have
, then we have

 , the above holds only if
, the above holds only if
 ,
i.e.,
,
i.e.,
 is the unique fixed point.
is the unique fixed point.








![$\displaystyle {\bf g}'({\bf x})={\bf J}_{\bf g}({\bf x})=\left[\begin{array}{cc...
... g_N}{\partial x_1}&\cdots&\frac{\partial g_N}{\partial x_N}
\end{array}\right]$](img234.svg)
 in the neighborhood of
in the neighborhood of  :
:

 is the remainder composed of second and higher
order terms of
is the remainder composed of second and higher
order terms of
 . Subtracting
. Subtracting
 and taking any p-norm on both sides, we get
and taking any p-norm on both sides, we get

 , the second and higher order terms
of
, the second and higher order terms
of
 disappear and
disappear and
 , we
have
, we
have

 , the function
, the function
 is a contraction at
is a contraction at  .
.



 , then
, then  is a contraction at
is a contraction at  .
.












 has zero derivative at the
fixed point
has zero derivative at the
fixed point  , we have
, we have

 constant
constant , then the iteration converges cubically.
, then the iteration converges cubically.








 , then we can define
, then we can define
 so that then
so that then
 , then the convergence becomes quadratic.
This is actually the Newton-Raphson method, to be discussed later.
, then the convergence becomes quadratic.
This is actually the Newton-Raphson method, to be discussed later.

 in two
different ways:
in two
different ways:
![$\displaystyle g_1(x)=x=\sqrt[3]{x+2},\;\;\;\;\;\;\;$](img262.svg) and
and
 (left) and
(left) and  (right) together with
(right) together with  and the identity function are plotted:
and the identity function are plotted:













 in two different ways:
in two different ways:
![$\displaystyle g_1(x)=x=\sqrt[3]{3x-1},\;\;\;\;\;\;g_2(x)=x=\frac{1}{3}(x^3-1)$](img273.svg)


 and
and  can be obtained by the iteration based on
can be obtained by the iteration based on
 and
and  can be obtained by the iteration based on
can be obtained by the iteration based on  .
But neither of them can find all three roots.
.
But neither of them can find all three roots.
 for all
for all
 except in the neighborhood of
except in the neighborhood of
 ,
i.e.,
,
i.e.,  is a contraction mapping everywhere except around
is a contraction mapping everywhere except around
 . Therefore the iteration starting from any initial guess
. Therefore the iteration starting from any initial guess
 will converge to either
will converge to either
 if
if  , or
, or
 if
if  .
.

 is not a contraction mapping around
is not a contraction mapping around  ,
the iteration will never converge to
,
the iteration will never converge to  .
.
 for all
for all
 except in the neighborhood of
except in the neighborhood of  , i.e.,
, i.e.,
 is not a contraction mapping around either
is not a contraction mapping around either  or
or  .
Therefore the iteration based on
.
Therefore the iteration based on  will not converge to
either
will not converge to
either  or
or  , but it may converge to
, but it may converge to  , if the initial
guess
, if the initial
guess  is in the range
is in the range
 . However, if
. However, if  is outside
this range the iteration will diverge toward either
is outside
this range the iteration will diverge toward either  if
if
 of
of  if
if  .
.



 in different ways:
in different ways:
![$\displaystyle g_0(x)=x=\sqrt[3]{\sin(x)},\;\;\;\;g'_0(x)=\frac{\cos(x)}{3\,\sin(x)^{2/3}}$](img291.svg)














![${\bf x}=[x,\;y,\;z]^T$](img306.svg)



![$\displaystyle {\bf J}_g=\left[\begin{array}{rrr}
0 & -1/2 & -1/3\\ -2/7 & 0 & -3/7\\ -1/5 & -3/5 & 0
\end{array}\right]$](img309.svg)
 .
Consequently, the iteration
.
Consequently, the iteration
 converges
from an initial guess
converges
from an initial guess
![${\bf x}_0=[1,\,1,\,1]^T$](img312.svg) to the solution
to the solution
![${\bf x}=[1,\,2,\,3]^T$](img313.svg) .
.

![$\displaystyle {\bf J}_{g'}=\left[ \begin{array}{rrr}
0 & -3 & -5\\ -2/7 & 0 & -3/7\\ -3 & -3/2 & 0
\end{array}\right]$](img315.svg)
 . The iteration does not
converge.
. The iteration does not
converge.

![${\bf x}=[x,\;y,\;z]^T$](img306.svg)


![${\bf x}_0=[0,\;0,\;0]^T$](img319.svg) and after
and after  iterations
iterations
 converges to
converges to
![${\bf x}_n=[1.098933,\;0.367621,\;0.144932]^T$](img321.svg) , with error
, with error
 . However, the iteration may
not converge from other possible initial guesses.
. However, the iteration may
not converge from other possible initial guesses.








 , we get
, we get

 to
to  , we move to the point
, we move to the point
 at which this secant line intersects with the identity function
at which this secant line intersects with the identity function  .
We can therefore replace
.
We can therefore replace  in the equation above by
in the equation above by  and solve the
resulting equation
and solve the
resulting equation


 and
and
 are respectively the first and second
order differences defined below:
are respectively the first and second
order differences defined below:



 , we skip
, we skip
 and
and
 but directly
move to
but directly
move to  computed based on
computed based on  and
and  , thereby making
a greater step towards the solution.
, thereby making
a greater step towards the solution.






