Solving equations by iteration

To solve a given equation $f(x)=0$, we can first convert it into an equivalent equation $g(x)=x$, and then carry out an iteration $x_{n+1}=g(x_n)$ from some initial value $x_0$. If the iteration converges at a point $x^*$, i.e., $g(x^*)=x^*$, then we also have $f(x^*)=0$, i.e., $x^*$ is also the root of the equation $f(x)=0$. Consider the following examples:

Example 1

To solve the equation

$$f(x)=\log(x)-0.5=0$$

we can first construct another function

$$g(x)=x-f(x)=x-\log(x)+0.5$$

so that the equation $g(x)=x$ is indeed equivalent to the given equation $f(x)=0$. We then carry out the iteration $x_{n+1}=g(x_n)$ from some initial value, such as $x_0=0.5$, and get:

$$\begin{array}{r\vert c\vert c\vert c}\hline n & x_n & g(x_n) ... ...\\ \hline 12& 1.64872 & 1.64872 & 0.00000 \\ \hline \end{array}$$

We see that the iteration converges to $x^*=\lim\limits_{n\rightarrow\infty} g(x_n)=1.64872$ satisfying $g(x^*)=x^*-f(x^*)=x^*$, and, equivalently, $x^*$ is also the solution of the given equation $f(x)=0.5-\log(x)=0$:

$$0.5-log(1.64872)=0,\;\;\;\;\;\;\; \;\;\;\;\;\; e^{0.5}=\sqrt{e}=1.64872$$

Alternatively, we could construct a different function

$$g(x)=x+f(x)=x+\log(x)-0.5$$

which is also equivalent to $f(x)=0$. But now the iteration no longer converges. Why does it not work?

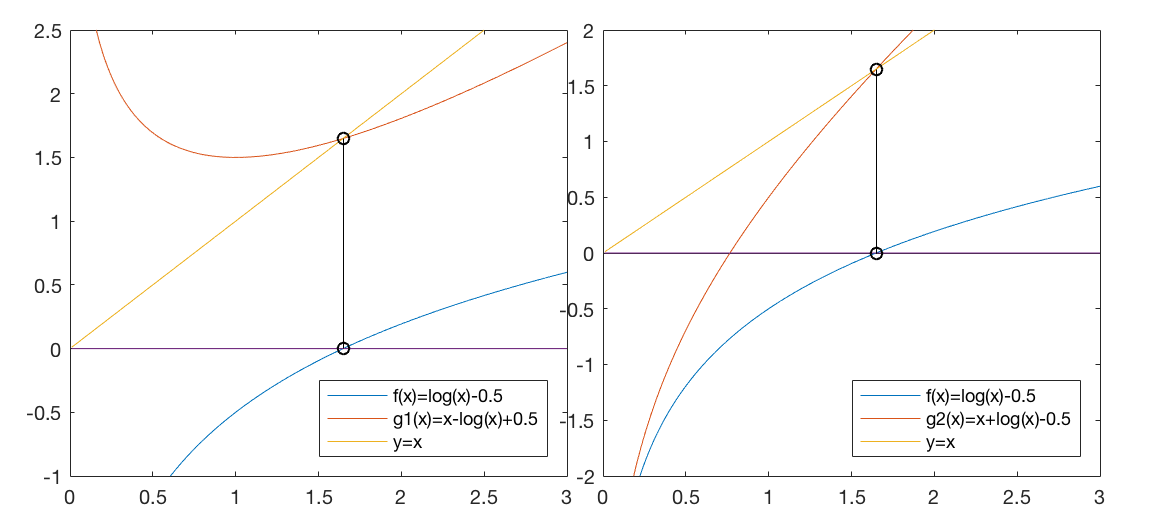
Example 2

$$f(x)=e^x-1/x=0$$

We first convert this equation into an equivalent form

$$g(x)=x=e^{-x}$$

and then carry out the iteration:

$$x_{n+1}=g(x_n)=e^{-x_n}\stackrel{n\rightarrow\infty}{\Longrightarrow} x^*=0.5671$$

which is the root of the given equation $f(x)=e^x-1/x=0$, i.e., $e^{-0.5671}=0.5671$.

Alternatively, the given equation can also be converted into a different form $g(x)=x=-\ln(x)$. However, the iteration based on this function no longer converges.

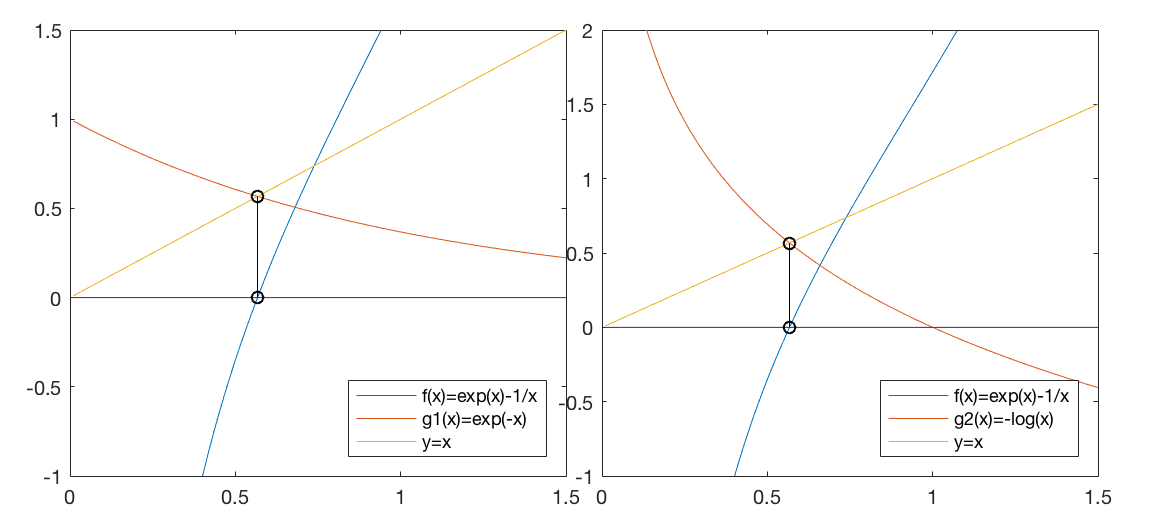
Example 3

$$f(x)=cos(x)-x=0$$

We define another equation:

$$g(x)=x=cos(x)$$

and the iteration based on $g(x)$ converges to the root of $f(x)=0$:

$$x_{n+1}=g(x_n)=cos(x_n)\stackrel{n\rightarrow\infty}{\Longrightarrow} 0.7391$$

i.e., $f(x_n)=\cos(x_n)-x_n=\cos(0.7391)-0.7391=0$ or $cos(0.7391)=0.7391$.

In summary, an equation $f(x)=0$ can be solved by converting it into an equivalent form $g(x)=x$, which can then be solved iteratively to find $x^*$ satisfying $g(x^*)=x^*$ and equivalently $f(x^*)=0$. However, this iteration may or may not converge, as shown by one of the examples above. We need to understand the condition for the convergence of the iteration, so that we can construct the function $g(x)$ properly for the iteration $g(x)=x$ to converge.