We next consider the complete solution (composed of both homogeneous
and particular solutions) of the 2nd order DE
 |
(232) |
with a unit step  input and zero initial conditions
input and zero initial conditions
 . As the input is a constant for
. As the input is a constant for  , we can
assume the particular solution to be a constant
, we can
assume the particular solution to be a constant  with zero
derivatives
with zero
derivatives
 . Substituting these into the DE above,
we get
. Substituting these into the DE above,
we get
 , i.e., the steady state solution is:
, i.e., the steady state solution is:
 |
(233) |
The complete response can be obtained as the sum of the homogeneous
solution (same as that obtained previously) and particular solution,
corresponding to the transient and steady state response, respectively:
 |
(234) |
The two coefficients  and
and  can be obtained based on the two
zero initial conditions:
can be obtained based on the two
zero initial conditions:
Solving these equations we get:
 |
(236) |
Now the complete solution becomes:
![$\displaystyle y(t)=\frac{1}{\omega_n^2}\left[1-\left(\frac{s_2e^{s_1t}}{s_2-s_1...
...ht]
=\frac{1}{\omega_n^2}\left(1-\frac{s_2e^{s_1t}-s_1e^{s_2t}}{s_2-s_1}\right)$](img670.svg) |
(237) |
Alternatively, the nonhomogeneous 2nd-order LCCODE given above can
be converted into a 1st-order ODE system and solving which we obtain
the same results, as shown
here.
The two roots  and
and  take different forms depending on
whether the discriminant
take different forms depending on
whether the discriminant
 is greater
or smaller than 0, i.e., whether
is greater
or smaller than 0, i.e., whether  is greater or smaller then 1.
Here we only consider the case when
is greater or smaller then 1.
Here we only consider the case when
 , i.e.,
, i.e.,  ,
for an under-damped second order system. The two roots are
,
for an under-damped second order system. The two roots are
 and and |
(238) |
where  is the damped natural frequency:
is the damped natural frequency:
 |
(239) |
Finally the complete solution of the non-homogeneous DE is:
where
 and and |
(241) |
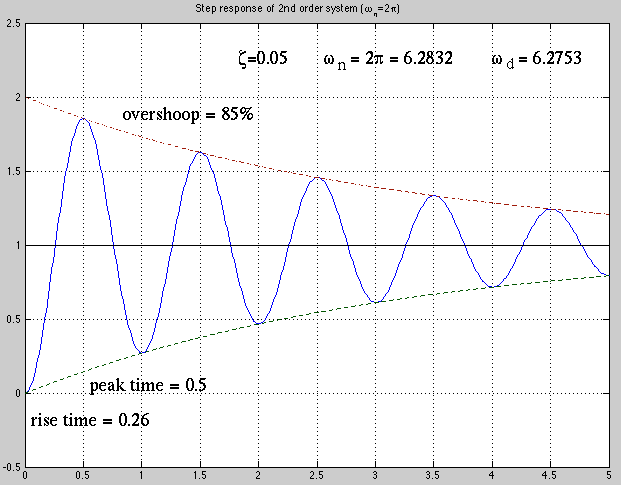
The step response  can be characterized by two parameters:
can be characterized by two parameters:
- Rise time:
The rise time  is the time at which
is the time at which  reaches
reaches  of the
steady state value
of the
steady state value  (assumed to be 1 for simplicity):
(assumed to be 1 for simplicity):
 or or |
(242) |
i.e.,
 or or |
(243) |
Solving for  we get
we get
 |
(244) |
But as
 , taking arctangent
on both sides we get
, taking arctangent
on both sides we get
 i.e. i.e. |
(245) |
- Peak time:
The peak time  is the time at which
is the time at which  reaches the first peak, which can be
found by setting the time derivative of
reaches the first peak, which can be
found by setting the time derivative of  to zero, yielding
to zero, yielding
 |
(246) |
i.e.,
 |
(247) |
or
 |
(248) |
We get
 for the first peak, i.e.,
for the first peak, i.e.,
 |
(249) |
Substituting  inito
inito  we get the peak value:
we get the peak value:
The overshoot is
 .
.
In particular, if  and therefore
and therefore  , we have
, we have
![$\displaystyle y(t)=\frac{1}{\omega_n^2}\left[1-\sin(\omega_n t+\pi/2)\right]
=\frac{1}{\omega_n^2}\left[1-\cos(\omega_n t)\right]$](img705.svg) |
(251) |
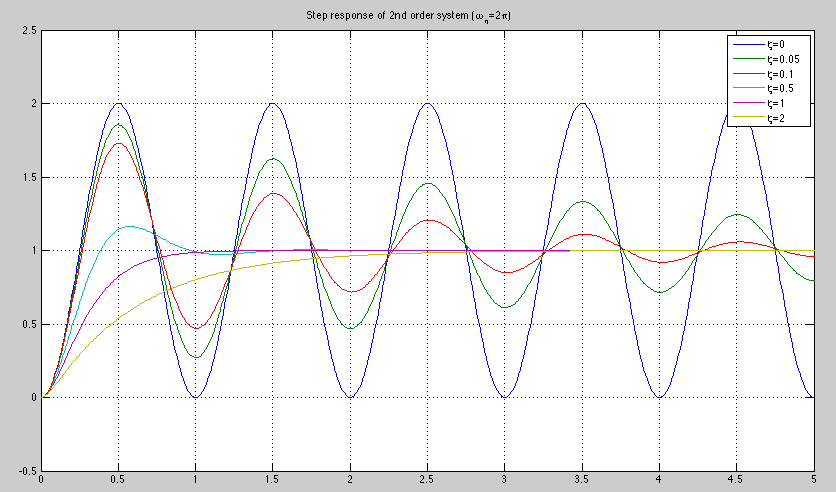
The plots below shows an example with
 . Note the critical
damped case when
. Note the critical
damped case when  . An overshoot will occur for any
. An overshoot will occur for any  .
.
The step response is plotted below. Note that  and
and
 .
.
Example
Consider the response
 of an undamped 2nd order RCL system.
of an undamped 2nd order RCL system.
- Find the response
 of the RLC circuit to a step input
of the RLC circuit to a step input
 .
The general solution is the sum of the homogeneous solution
.
The general solution is the sum of the homogeneous solution
 and the particular solution
and the particular solution  :
:
 |
(252) |
Consider two different sets of initial conditions:
- Find the system's response to a square impulse
 |
(255) |
As
 , the response is
, the response is
![$\displaystyle y(t)=[1-\cos(\omega_nt)]u(t)-[1-\cos(\omega_n(t-t_0))]u(t-t_0)$](img724.svg) |
(256) |
When  , we have
, we have
 |
(257) |
We further consider two special cases.
- When
 , we have
, we have
This is a one period of a sinusoid.
- When
 , we have
, we have
This is a pure sinusoid after  .
.
- Find the impulse response
 . The input
. The input  is an impulse which
can be written as
is an impulse which
can be written as
 |
(260) |
When
 , we have first order approximations
, we have first order approximations
 and
and
 ,
and we get
,
and we get
 |
(261) |
Substituting this into
 we get the impulse response
we get the impulse response
 |
(262) |
- It is often desirable for a second order system to reach a set steady
state value without overshoot. This can be achieved by driving the system
by an impulse
 with response
with response
 , followed
by a step
, followed
by a step  with response
with response
![$\displaystyle [1-\cos(\omega_n(t-T/4))]u(t-T/4)=[1-\cos(\omega_nt-\pi/2)]u(t-T/4)
=[1-\sin(\omega_nt)]u(t-T/4)$](img746.svg) |
(263) |
The total response is
![$\displaystyle y(t)=\sin(\omega_nt)u(t)+[1-\sin(\omega_nt)]u(t-T/4)
=\left\{\begin{array}{cl} \sin(\omega_nt) & 0<t<T/4 \\
1 & t>T/4\end{array} \right.$](img747.svg) |
(264) |
We see that after  reaches the first peak of
reaches the first peak of  at
at  , it will
stay at the constant value
, it will
stay at the constant value  as the two responses cancel each other for
as the two responses cancel each other for
 .
.
- Alternatively, the steady state value
 can be achieved without
overshoot by applying an input
can be achieved without
overshoot by applying an input
![$x(t)=[u(t)-u(t-T/2)]/2$](img752.svg) . The response to
. The response to
 is
is
![$\displaystyle \frac{1}{2}[1-\cos(\omega_nt)]u(t)$](img754.svg) |
(265) |
while the response to
 is
is
![$\displaystyle \frac{1}{2}[1-\cos(\omega_n(t-T/2))]u(t-T/2)
=\frac{1}{2}[1-\cos(\omega_nt-\pi)]u(t-T/2)
=\frac{1}{2}[1+\cos(\omega_nt)]u(t-T/2)$](img756.svg) |
(266) |
The overall response is the difference between the two individual responses:
![$\displaystyle y(t)=\left\{\begin{array}{cl}
[1-\cos\omega_nt]/2 & 0<t<T/2 \\ 1 & t>T/2 \end{array} \right.$](img757.svg) |
(267) |
i.e., the response is  for all
for all  .
.
- It is desirable for a second order system to reach a steady state value
 within a time delay
within a time delay  without overshoot. We first consider
driving the system with a positive square pulse of value
without overshoot. We first consider
driving the system with a positive square pulse of value  followed
by a negative one of
followed
by a negative one of  :
:
![$\displaystyle x(t)=\left\{\begin{array}{cl}
V & (0<t<t_0/2) \\ (1-a)V & (t_0/2<t<t_0)
\end{array}\right. =V \left[u(t)-a u(t-t_0/2)\right]$](img762.svg) |
(268) |
The response for
 is:
is:
![$\displaystyle y(t)=V\left[ 1-\cos(\omega_nt)-a[1-\cos(\omega_n(t-t_0/2))]\right]$](img764.svg) |
(269) |
In order for the output to be a constant  for
for  , we need to
have the input
, we need to
have the input  for
for  , and set the initial conditions at
, and set the initial conditions at  to be
to be  and
and
 . To do so, we let
. To do so, we let
![$\displaystyle \frac{dy(t)}{dt}\bigg\vert _{t=t_0}=V\omega_n\left[ \sin(\omega_n...
...right]_{t=t_0}
=V\omega_n\left[ \sin(\omega_nt_0)-a\sin(\omega_nt_0/2)\right]=0$](img769.svg) |
(270) |
Based on the trigonometric identity
 , the equation above
can be written as
, the equation above
can be written as
 |
(271) |
Substituting this into the desired initial condition  , we get
, we get
![$\displaystyle y(t_0)=V\left[ 1-\cos(\omega_nt_0)-2\cos(\omega_nt_0/2)
[1-\cos(\omega_n(t_0/2))]\right]
=2V(1-\cos(\omega_nt_0/2) =4V\sin^2(\omega_nt_0/4)=1$](img772.svg) |
(272) |
where we have used the trigonometric identities
 and
and
 . Solving this for
. Solving this for  we get
we get
 |
(273) |
As now we have the initial conditions  and
and
 as
needed. If we set
as
needed. If we set  for
for  , so that the output will be at
constant
, so that the output will be at
constant  when
when  .
.

 input and zero initial conditions
input and zero initial conditions
 . As the input is a constant for
. As the input is a constant for  , we can
assume the particular solution to be a constant
, we can
assume the particular solution to be a constant  with zero
derivatives
with zero
derivatives
 . Substituting these into the DE above,
we get
. Substituting these into the DE above,
we get
 , i.e., the steady state solution is:
, i.e., the steady state solution is:


 and
and  can be obtained based on the two
zero initial conditions:
can be obtained based on the two
zero initial conditions:







![$\displaystyle y(t)=\frac{1}{\omega_n^2}\left[1-\left(\frac{s_2e^{s_1t}}{s_2-s_1...
...ht]
=\frac{1}{\omega_n^2}\left(1-\frac{s_2e^{s_1t}-s_1e^{s_2t}}{s_2-s_1}\right)$](img670.svg)






 and
and
 is the damped natural frequency:
is the damped natural frequency:



![$\displaystyle \frac{1}{\omega_n^2}\left[1-\left(\frac{s_2}{s_2-s_1}e^{s_1t}-\frac{s_1}{s_2-s_1}e^{s_2t}\right)\right]$](img677.svg)

![$\displaystyle \frac{1}{\omega_n^2}\left[ 1-
\left(\frac{\zeta+j\sqrt{1-\zeta^2}...
...1-\zeta^2}}{2j\sqrt{1-\zeta^2}} e^{(-\zeta\omega_n-j\omega_d)t} \right) \right]$](img678.svg)

![$\displaystyle \frac{1}{\omega_n^2}\left[ 1-\frac{e^{-\zeta\omega_nt}}{\sqrt{1-\...
...j\omega_dt}
-\frac{\zeta-j\sqrt{1-\zeta^2}}{2j} e^{-j\omega_dt} \right) \right]$](img679.svg)

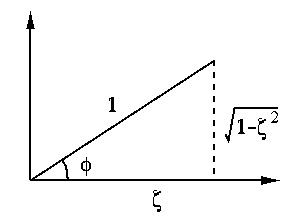
![$\displaystyle \frac{1}{\omega_n^2}\left[ 1-\frac{e^{-\zeta\omega_nt}}{\sqrt{1-\...
...rac{ e^{j\phi} e^{ j\omega_dt}-e^{-j\phi} e^{-j\omega_dt} }{2j} \right) \right]$](img680.svg)

![$\displaystyle \frac{1}{\omega_n^2}\left[1-\frac{e^{-\zeta\omega_nt}}{\sqrt{1-\zeta^2}}
\sin(\omega_dt+\phi) \right]$](img681.svg)
 and
and






 or
or
 or
or
 we get
we get

 , taking arctangent
on both sides we get
, taking arctangent
on both sides we get
 i.e.
i.e.






 for the first peak, i.e.,
for the first peak, i.e.,

 inito
inito  we get the peak value:
we get the peak value:





 .
.


![$\displaystyle y(t)=\frac{1}{\omega_n^2}\left[1-\sin(\omega_n t+\pi/2)\right]
=\frac{1}{\omega_n^2}\left[1-\cos(\omega_n t)\right]$](img705.svg)








 of the RLC circuit to a step input
of the RLC circuit to a step input
 .
The general solution is the sum of the homogeneous solution
.
The general solution is the sum of the homogeneous solution
 and the particular solution
and the particular solution  :
:

 . We have
. We have
 and
and
 , and
, and
![$\displaystyle y(t)=V+A\sin(\omega_nt)+B\cos(\omega_nt)=V[1-\cos(\omega_nt)]$](img716.svg)
 ,
,  . We have
. We have
 and
and
 ,
i.e.,
,
i.e.,  and
and


 , the response is
, the response is
![$\displaystyle y(t)=[1-\cos(\omega_nt)]u(t)-[1-\cos(\omega_n(t-t_0))]u(t-t_0)$](img724.svg)
 , we have
, we have

 , we have
, we have


![$\displaystyle [1-\cos(\omega_nt)]u(t)-[1-\cos(\omega_n(t-T))]u(t-T)$](img728.svg)


 , we have
, we have


![$\displaystyle [1-\cos(\omega_nt)]u(t)-[1-\cos(\omega_n(t-T/2))]u(t-T/2)$](img731.svg)

![$\displaystyle [1-\cos(\omega_nt)]u(t)-[1+\cos(\omega_nt)]u(t-T/2)$](img732.svg)


 .
.
 . The input
. The input  is an impulse which
can be written as
is an impulse which
can be written as

 , we have first order approximations
, we have first order approximations
 and
and
 ,
and we get
,
and we get

 we get the impulse response
we get the impulse response

 with response
with response
 , followed
by a step
, followed
by a step  with response
with response
![$\displaystyle [1-\cos(\omega_n(t-T/4))]u(t-T/4)=[1-\cos(\omega_nt-\pi/2)]u(t-T/4)
=[1-\sin(\omega_nt)]u(t-T/4)$](img746.svg)
![$\displaystyle y(t)=\sin(\omega_nt)u(t)+[1-\sin(\omega_nt)]u(t-T/4)
=\left\{\begin{array}{cl} \sin(\omega_nt) & 0<t<T/4 \\
1 & t>T/4\end{array} \right.$](img747.svg)
 reaches the first peak of
reaches the first peak of  at
at  , it will
stay at the constant value
, it will
stay at the constant value  as the two responses cancel each other for
as the two responses cancel each other for
 .
.
 can be achieved without
overshoot by applying an input
can be achieved without
overshoot by applying an input
![$x(t)=[u(t)-u(t-T/2)]/2$](img752.svg) . The response to
. The response to
 is
is
![$\displaystyle \frac{1}{2}[1-\cos(\omega_nt)]u(t)$](img754.svg)
 is
is
![$\displaystyle \frac{1}{2}[1-\cos(\omega_n(t-T/2))]u(t-T/2)
=\frac{1}{2}[1-\cos(\omega_nt-\pi)]u(t-T/2)
=\frac{1}{2}[1+\cos(\omega_nt)]u(t-T/2)$](img756.svg)
![$\displaystyle y(t)=\left\{\begin{array}{cl}
[1-\cos\omega_nt]/2 & 0<t<T/2 \\ 1 & t>T/2 \end{array} \right.$](img757.svg)
 for all
for all  .
.
 within a time delay
within a time delay  without overshoot. We first consider
driving the system with a positive square pulse of value
without overshoot. We first consider
driving the system with a positive square pulse of value  followed
by a negative one of
followed
by a negative one of  :
:
![$\displaystyle x(t)=\left\{\begin{array}{cl}
V & (0<t<t_0/2) \\ (1-a)V & (t_0/2<t<t_0)
\end{array}\right. =V \left[u(t)-a u(t-t_0/2)\right]$](img762.svg)
 is:
is:
![$\displaystyle y(t)=V\left[ 1-\cos(\omega_nt)-a[1-\cos(\omega_n(t-t_0/2))]\right]$](img764.svg)
 for
for  , we need to
have the input
, we need to
have the input  for
for  , and set the initial conditions at
, and set the initial conditions at  to be
to be  and
and
 . To do so, we let
. To do so, we let
![$\displaystyle \frac{dy(t)}{dt}\bigg\vert _{t=t_0}=V\omega_n\left[ \sin(\omega_n...
...right]_{t=t_0}
=V\omega_n\left[ \sin(\omega_nt_0)-a\sin(\omega_nt_0/2)\right]=0$](img769.svg)
 , the equation above
can be written as
, the equation above
can be written as

 , we get
, we get
![$\displaystyle y(t_0)=V\left[ 1-\cos(\omega_nt_0)-2\cos(\omega_nt_0/2)
[1-\cos(\omega_n(t_0/2))]\right]
=2V(1-\cos(\omega_nt_0/2) =4V\sin^2(\omega_nt_0/4)=1$](img772.svg)
 and
and
 . Solving this for
. Solving this for  we get
we get

 and
and
 as
needed. If we set
as
needed. If we set  for
for  , so that the output will be at
constant
, so that the output will be at
constant  when
when  .
.