The homogeneous solution of the 2nd order DE can be found
by solving the homogeneous equation:
 |
(209) |
where the right hand side of the DE for the input  is
zero. Substituting the assumed solution
is
zero. Substituting the assumed solution
 and its
derivatives
and its
derivatives
 into
the DE we get
into
the DE we get
 |
(210) |
As we are not interested in a trivial solution,
 , and
we get an algebraic equation
, and
we get an algebraic equation
 |
(211) |
Solving this quadratic equation we get its two roots, the two
eigenvalues of  :
:
 |
(212) |
where
 |
(213) |
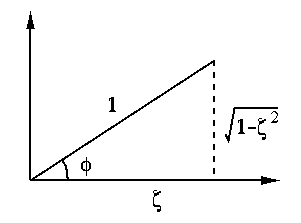
These two roots  are either two real numbers or a pair
complex conjugate numbers, depending on whether its discriminant
is greater and smaller then 0:
are either two real numbers or a pair
complex conjugate numbers, depending on whether its discriminant
is greater and smaller then 0:
 |
(214) |
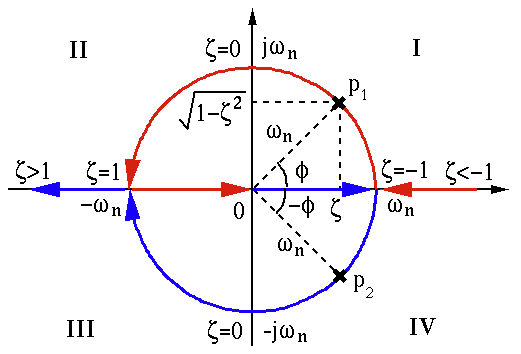
For a constant  and a variable
and a variable  that changes
from
that changes
from  to
to  , the two roots
, the two roots  (red) and
(red) and  (blue) can be represented as the root locus on the complex plane.
(blue) can be represented as the root locus on the complex plane.
In particular, for the RCL circuit with all  ,
,  , and
, and  values
non-negative, we have
values
non-negative, we have
 , i.e., we only need to consider the
root locus on the left side of the complex plain.
, i.e., we only need to consider the
root locus on the left side of the complex plain.
Given the two roots  and
and  , we can write the homogeneous
solution as
, we can write the homogeneous
solution as
 |
(215) |
where the two coefficients  and
and  can be found based on the
two initial conditions
can be found based on the
two initial conditions  and
and  . If we assume
. If we assume
 but
but  , then we get
, then we get
Solving these we get
 |
(217) |
and the homogeneous solution becomes:
![$\displaystyle y_h(t)=y_0 \left[ \frac{s_2 e^{s_1t}}{s_2-s_1}-\frac{s_1 e^{s_2t}}{s_2-s_1} \right]
=\frac{y_0}{s_2-s_1} (s_2 e^{s_1t}-s_1 e^{s_2t})$](img631.svg) |
(218) |
Alternatively, the 2nd-order LCCODE in canonical form given above can
also be solved if it is coverted into a 1st-order ODE system, as
shown here.
The solution takes different forms depending on the value of the damping
coefficient  .
.
- Over-damped system (
 )
)
This is a sum of two exponentially decaying terms, without any overshoot
or oscillation. Note that when  ,
,  .
.
- Critically damped system (
 )
)
Now we have
 |
(220) |
and the homogeneous solution takes following form:
Applying the initial conditions to this response we get
Solving this we get if
 :
:
 |
(223) |
and the response is
![$\displaystyle y_h(t)=C_1 e^{st}+C_2 t e^{st}=y_0\left[ e^{-\omega_nt}+\omega_n t e^{-\omega_nt}\right]$](img646.svg) |
(224) |
Again, there is no overshoot or oscillation.
- Under-damped system (
 )
)
 and and |
(225) |
where  is the damped natural frequency defined as:
is the damped natural frequency defined as:
 |
(226) |
The response is
Here we have defined:
 |
(228) |
- Undamped system (
 and
and  )
)
 |
(229) |
![$\displaystyle y_h(t)=y_0 \left[ \frac{s_2 e^{s_1t}}{s_2-s_1}+\frac{s_1 e^{s_2t}...
...ght]
=y_0\left(\frac{e^{j\omega_n}+e^{-j\omega_n}}{2}\right)=y_0\cos(\omega_nt)$](img657.svg) |
(230) |
This result can also be obtained from the previous case:
 |
(231) |
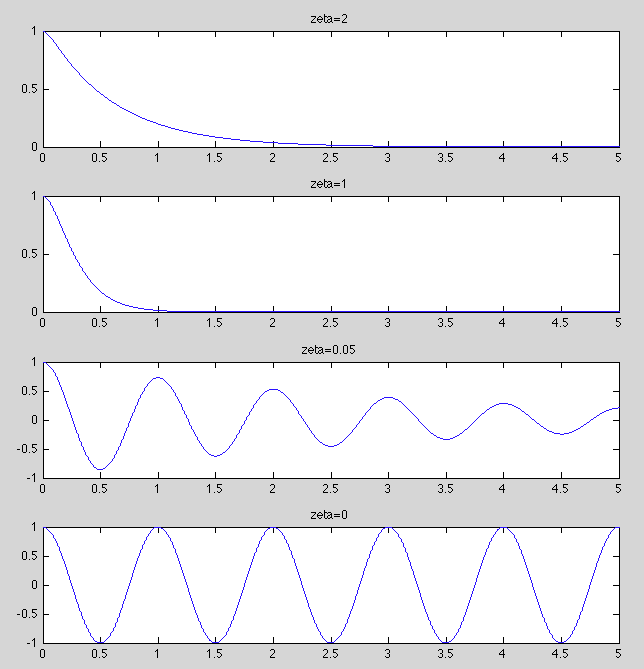
The homogeneous responses of these four cases are plotted below. Note that in all cases,
 and
and
 .
.

 is
zero. Substituting the assumed solution
is
zero. Substituting the assumed solution
 and its
derivatives
and its
derivatives
 into
the DE we get
into
the DE we get

 , and
we get an algebraic equation
, and
we get an algebraic equation

 :
:



















 and
and  can be found based on the
two initial conditions
can be found based on the
two initial conditions  and
and  . If we assume
. If we assume
 but
but  , then we get
, then we get







![$\displaystyle y_h(t)=y_0 \left[ \frac{s_2 e^{s_1t}}{s_2-s_1}-\frac{s_1 e^{s_2t}}{s_2-s_1} \right]
=\frac{y_0}{s_2-s_1} (s_2 e^{s_1t}-s_1 e^{s_2t})$](img631.svg)

 )
)


![$\displaystyle y_0 \left[ \frac{s_2 e^{s_1t}}{s_2-s_1}+\frac{s_1 e^{s_2t}}{s_1-s_2} \right]$](img634.svg)

![$\displaystyle y_0\left[\frac{-\zeta+\sqrt{\zeta^2-1}}{2\sqrt{\zeta^2-1}}e^{(-\z...
...qrt{\zeta^2-1}}{2\sqrt{\zeta^2-1}}e^{(-\zeta+\sqrt{\zeta^2-1})\omega_nt}\right]$](img635.svg)
 ,
,  .
.
 )
)






![$\displaystyle \frac{d}{dt}[C_1 e^{st}+C_2 t e^{st}]=C_1se^{st}+C_2(e^{st}+ste^{st})$](img641.svg)






 :
:

![$\displaystyle y_h(t)=C_1 e^{st}+C_2 t e^{st}=y_0\left[ e^{-\omega_nt}+\omega_n t e^{-\omega_nt}\right]$](img646.svg)
 )
)
 and
and
 is the damped natural frequency defined as:
is the damped natural frequency defined as:



![$\displaystyle y_0 \left[ \frac{s_2 e^{s_1t}}{s_2-s_1}+\frac{s_1 e^{s_2t}}{s_1-s_2} \right]$](img634.svg)

![$\displaystyle y_0\left[ \frac{(-\zeta-j\sqrt{1-\zeta^2})\omega_n}{-2j\omega_n\s...
...)\omega_n}{-2j\omega_n\sqrt{1-\zeta^2}} e^{(-\zeta\omega_n-j\omega_d)t} \right]$](img652.svg)



 and
and  )
)

![$\displaystyle y_h(t)=y_0 \left[ \frac{s_2 e^{s_1t}}{s_2-s_1}+\frac{s_1 e^{s_2t}...
...ght]
=y_0\left(\frac{e^{j\omega_n}+e^{-j\omega_n}}{2}\right)=y_0\cos(\omega_nt)$](img657.svg)



