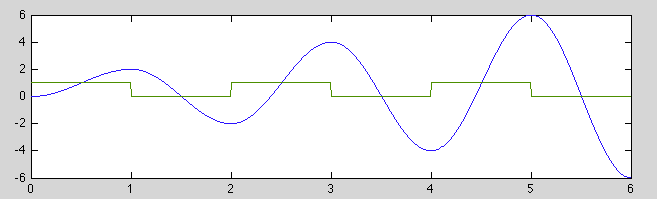
Example 1
Consider the steady state response of a first order RC circuit with the
parameter  to a square impulse train of period
to a square impulse train of period  :
:
 |
(274) |
where  is the on-time and
is the on-time and  is off-time of the impulse train.
Consider the response
is off-time of the impulse train.
Consider the response
 during both the on and off periods:
during both the on and off periods:
- The on-time response can be found based on the assumed initial condition
 :
:
 |
(275) |
In particular,

- The off-time response can be found based on the initial condition
 to be
to be
 |
(276) |
In particular,

The two voltages  and
and  can then be found by solving these two
simultaneous equations:
can then be found by solving these two
simultaneous equations:
 |
(277) |
Substituting the first equation into the second one we can find  and then
and then
 :
:
 |
(278) |
Consider some special cases:
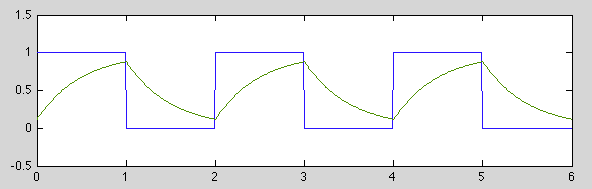
Here
 ,
,  .
.
Example 2
Consider the steady state response of an undamped second order system with
parameters  and
and  to a symmetric square impulse train of
period
to a symmetric square impulse train of
period  :
:
 |
(282) |
where  is both the on and off-time of the impulse train, which can also
be written as:
is both the on and off-time of the impulse train, which can also
be written as:
 |
(283) |
The response of the 2nd order system can be obtained based on its step
response
 (with some constant coefficient which
is neglected):
(with some constant coefficient which
is neglected):
-
 |
(284) |
-
 |
(285) |
-
-
We now consider two special cases:



 is the on-time and
is the on-time and  is off-time of the impulse train.
Consider the response
is off-time of the impulse train.
Consider the response
 during both the on and off periods:
during both the on and off periods:
 :
:


 to be
to be


 and
and  can then be found by solving these two
simultaneous equations:
can then be found by solving these two
simultaneous equations:

 and then
and then
 :
:

 and
and
 , all exponential terms become zero
and we have
, all exponential terms become zero
and we have  and
and  , i.e., the capacitor is fully charged and
then fully discharged.
, i.e., the capacitor is fully charged and
then fully discharged.
 and
and
 , all exponential terms can be
approximated by
, all exponential terms can be
approximated by
 , and we have:
, and we have:

 , we have
, we have









 is both the on and off-time of the impulse train, which can also
be written as:
is both the on and off-time of the impulse train, which can also
be written as:

 (with some constant coefficient which
is neglected):
(with some constant coefficient which
is neglected):












 is the same as the natural period of
the 2nd order system, then
is the same as the natural period of
the 2nd order system, then
 and we have
the following for all integer
and we have
the following for all integer  :
:


 , more terms will be included in
, more terms will be included in
 , which is zero when an even number of terms are included, but
, which is zero when an even number of terms are included, but
 when an odd number of terms are included.
when an odd number of terms are included.
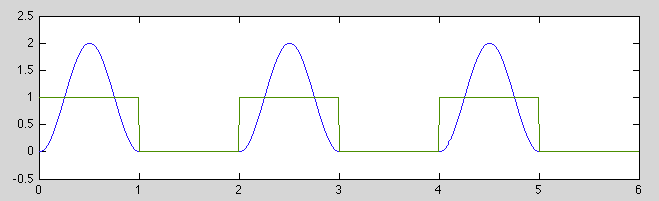
 , the period
, the period  of the impulse train is
the same as the natural period
of the impulse train is
the same as the natural period
 of the 2nd system,
of the 2nd system,