


Next: About this document ...
The canonical 2nd-order LCCODE
caan be converted into a 1st-order ODE system containing two
1st-order LCCODEs (see
here):
The characteristic equation of the coefficient matrix 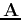 is
is
Solving which we get the two eigenvalues and the eigenvalue matrix:
Note that
The eigenvector matrix and its inverse are:
and we can verify thatat
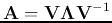 .
.
- Homogeneous solution
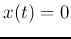 :
:
Assuming
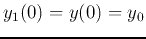 and
and
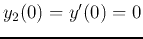 , we get the homogeneous
solution:
, we get the homogeneous
solution:
we get the same result as shown above:
- Nonhomogeneous sollution
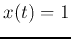 , i.e.,
, i.e.,
![${\bf x}=[0,\;1]^T$](img19.png) :
:
Assuming zero-initial condition
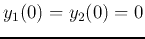 , i.e.,
, i.e.,
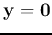 ,
the non-homogeneous solution is:
,
the non-homogeneous solution is:
where
Substituting
into the function, we get



Next: About this document ...
Ruye Wang
2019-03-15
![\begin{displaymath}
{\bf y}'=\left[\begin{array}{c}y_1' y_2'\end{array}\right]...
...t[\begin{array}{c}0 x(t)\end{array}\right]
={\bf Ay}+{\bf x}
\end{displaymath}](img2.png)
![\begin{displaymath}
\det(\lambda{\bf I}-{\bf A})
=\det\left[\begin{array}{cc}\la...
...nd{array}\right]
=\lambda^2+2\zeta\omega_n\lambda+\omega_n^2=0
\end{displaymath}](img4.png)
![\begin{displaymath}
\lambda_{1,2}=(-\zeta\pm\sqrt{\zeta^2-1})\omega_n
\;\;\;\;\;...
...egin{array}{cc}\lambda_1 & 0 0 & \lambda_2\end{array}\right]
\end{displaymath}](img5.png)
![\begin{displaymath}
{\bf V}=\left[\begin{array}{cc}1 & 1 \lambda_1 & \lambda_2...
...in{array}{cc}\lambda_2 & -1 -\lambda_1 & 1\end{array}\right]
\end{displaymath}](img7.png)
![]() and
and
![]() , we get the homogeneous
solution:
, we get the homogeneous
solution:
![$\displaystyle e^{{\bf A}t}{\bf y}(0)={\bf V}e^{{\bf\Lambda}t}{\bf V}^{-1}{\bf y...
...ambda_1&1\end{array}\right]
\left[\begin{array}{c} y_0 0\end{array}\right]$](img14.png)
![$\displaystyle \frac{1}{\lambda_2-\lambda_1}
\left[\begin{array}{cc} \lambda_2e...
...ambda_1t}\end{array}\right]
\left[\begin{array}{c} y_0 0\end{array}\right]$](img15.png)
![$\displaystyle \frac{y_0}{\lambda_2-\lambda_1}
\left[\begin{array}{c} \lambda_2...
..._2t}\\
\lambda_1\lambda_2(e^{\lambda_1t}-e^{\lambda_2t})
\end{array}\right]$](img16.png)
![]() , i.e.,
, i.e.,
![]() ,
the non-homogeneous solution is:
,
the non-homogeneous solution is:
![$\displaystyle [1,\;0]\;\left(e^{{\bf A}t}\int_0^t e^{-{\bf A}\tau} d\tau\right)...
...}\right)
\left({\bf I}-{\bf V}e^{-{\bf\Lambda}t}{\bf V}^{-1}\right)\;[0,\;1]^T$](img27.png)
![$\displaystyle [1,\;0]\;\left[\begin{array}{cc}1&1 \lambda_1&\lambda_2\end{ar...
... -\lambda_1&1\end{array}\right]
\left[\begin{array}{c}0 1\end{array}\right]$](img29.png)
![$\displaystyle \left[e^{\lambda_1t},\;e^{\lambda_2t}\right]
\left[\begin{array}...
...ac{\lambda_2e^{\lambda_1t}-\lambda_1e^{\lambda_2t}}{\lambda_2-\lambda_1}\right)$](img30.png)