Steady State Solution and Resonance

If only the steady state response of a second order system is of interest, then we can ignore the homogeneous solution due to the initial condition and consider only the particular solution due to the input. To do so, we convert the 2nd order DE into an algebraic equation in terms of the impedances of the components. In the following, we consider first the series system and then the parallel system.

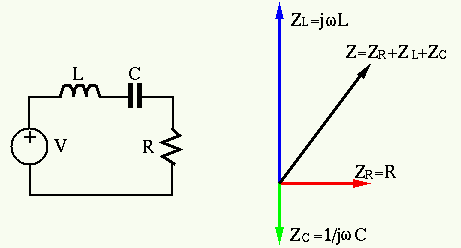
Series system: The overall impedance of the three elements is

$$Z=R+j\omega L+\frac{1}{j\omega C}=R+j\left(\omega L-\frac{1}{\omega C}\right) =\vert Z\vert e^{j\angle Z}$$ (183)

where

$$\vert Z\vert=\sqrt{R^2+\left(\omega L-\frac{1}{\omega C}\right)^2... ...mega \rightarrow \infty\;\; (Z_L=\infty,\;\mbox{inductive}) \end{array} \right.$$ (184)

$$\angle Z=\tan^{-1} \left(\frac{\omega L-1/\omega C}{R}\right) =\l... ... & \omega \rightarrow \infty\;\; (Z_C=0,\;\mbox{inductive}) \end{array} \right.$$ (185)

The impedance $Z=Z_R+Z_C+Z_L$ as a function of frequency $\omega$ is plotted below:

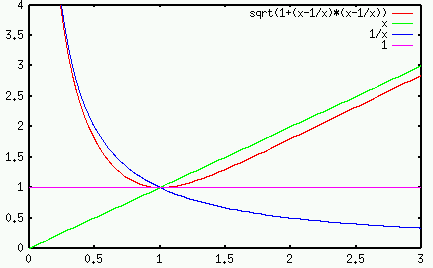
In particular, at the natural frequency $\omega=\omega_n=1/\sqrt{LC}$, the impedances of the capacitor and the inductor have the same magnitude $\omega L=1/\omega C$ but opposite phase, and their sum is zero $Z_L+Z_C=0$, i.e.,

$$Z_L=j\omega_nL=j\sqrt{\frac{L}{C}},\;\;\;\;\;\; Z_C=\frac{1}{j\omega_nC}=-j\sqrt{\frac{L}{C}},\;\;\;\;\; Z_L+Z_C=0$$ (186)

In this case, the RLC circuit is said to be in resonance, with the total impedance $Z=Z_R+Z_C+Z_L=Z_R=R$ minimized and the current $\dot{I}=\dot{V}/Z=\dot{V}/R$ maximized. Also, as the total impedance has a zero phase angle $\angle Z=\angle R=0$, the current $\dot{I}$ and voltage $\dot{V}$ are in phase. More specially, if $R\rightarrow 0$, then the total impedance is $Z\rightarrow 0$, i.e., the current $\dot{I}\rightarrow \infty$.

The quality factor of this series RCL 2nd order system is defined as

$$Q_s = \frac{\mbox{Magnitude of inductor/capacitor impedance at $\omega_n$}} {\mbox{Resistance}}$$

$$= \frac{\vert Z_L\vert}{R}=\frac{\omega_nL}{R}=\frac{L}{R\sqrt{LC}} =\frac{1}{R}\sqrt{\frac{L}{C}}=\frac{1}{2\zeta_s}$$

$$= \frac{\vert Z_C\vert}{R}=\frac{1}{\omega_nCR}=\frac{\sqrt{LC}}{RC} =\frac{1}{R}\sqrt{\frac{L}{C}}=\frac{1}{2\zeta_s}$$ (187)

Consider the voltages across the three components at natural when $\omega=\omega_n=1/\sqrt{LC}$:

$$\dot{V}_R=\dot{I} Z_R =\frac{\dot{V}}{R} \;R=\dot{V}$$ (188)

$$\dot{V}_L=\dot{I} Z_L=\frac{\dot{V}}{R}\;j\omega_n L =j\frac{\dot{V}}{R}\;\frac{L}{\sqrt{LC}} =j\,\dot{V} \frac{1}{R}\sqrt{\frac{L}{C}}=jQ_s\dot{V}$$ (189)

$$\dot{V}_C=\dot{I} Z_C=\frac{\dot{V}}{R}\;\frac{1}{j\omega_n C} =-... ...}\;\frac{\sqrt{LC}}{C} =-j\,\dot{V}\;\frac{1}{R}\sqrt{\frac{L}{C}}=-jQ_s\dot{V}$$ (190)

We see that

• The voltage across $R$ is equal to the source voltage $\dot{V}_R=\dot{V}$
• The voltages across $L$ and $C$ have the same magnitude, which is $Q_s$ times the input voltage $\vert\dot{V}_L\vert=\vert\dot{V}_C\vert=Q_s\dot{V}$
• The voltage across $L$ and $C$ have opposite phases: $\angle V_L=-\angle V_C$.

We see that $\dot{V}_L=-\dot{V}_C$, i.e., $V_L$ and $V_C$ have opposite polarities and they cancel each other.

Example: In a series RLC circuit, $R=5\Omega$, $L=4\;mH$ and $C=0.1\;\mu F$. The natural frequency $\omega_n$ can be found to be $\omega_n=1/\sqrt{LC}=1/\sqrt{4\times 10^{-3}\times 10^{-7}}=5\times 10^4$. The quality factor is

$$Q_s=\frac{\omega_nL}{R}=\frac{(5\times 10^4)\times (4\times 10^{-3})}{5} =40$$ (191)

or

$$Q_s=\frac{1}{\omega_nCR}=\frac{1}{(5\times 10^4)\times 10^{-7}\times 5} =40$$ (192)

If the input voltage is $V_{rms}=10V$ at the natural frequency, the current is $I=V/R=10/5=2 A$, and the voltages across each of the elements are:

• $\dot{V}_R=R\dot{I}=V=10V$
• $\dot{V}_L=j\omega L \dot{I}=j5\times 10^4\times 4\times 10^{-3} \times 2=j400V=jQ_sV$
• $\dot{V}_C=\dot{I}/j\omega_nC=-j2/(5\times 10^4\times 0.1\times 10^{-6})=-j400V=-jQ_sV$

Note that although input voltage is $10V$, the voltage across L and C ($Q$ times the input) could be very high, but they are in opposite phase and therefore cancel each other).

Parallel system:

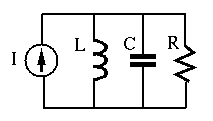
The overall admittance of the three elements in parallel is

$$Y=G+j\omega C+\frac{1}{j\omega L}=G+j\left(\omega C-\frac{1}{\omega L}\right) =\vert Y\vert e^{j\angle Y}$$ (193)

where

$$\vert Y\vert=\sqrt{G^2+\left(\omega C-\frac{1}{\omega L}\right)^2},\;\;\;\; \angle Y=\tan^{-1} \left(\frac{\omega C-1/\omega L}{G}\right)$$ (194)

In particular when $\omega=\omega_n=1/\sqrt{LC}$, we have $\omega C=1/\omega L$, and the total admittance is minimized (impedance is maximized):

$$Y=Y_R+Y_C+Y_L=G+j\left(\omega C-\frac{1}{\omega L}\right)=G$$ (195)

and the voltage $\dot{V}=\dot{I}/Y=\dot{I}/G$ is maximized. Also, as $\angle Y=0$, the voltage $\dot{V}$ and current $\dot{I}$ are in phase.

The quality factor $Q_p$ of this parallel RCL 2nd order system is defined as

$$Q_p = \frac{\mbox{Magnitude of inductor/capacitor susceptance at $\omega_n$}} {\mbox{Conductance}}$$

$$= \frac{\vert Y_L\vert}{G}=\frac{1}{\omega_nLG}=\frac{\sqrt{LC}}{LG} =R\sqrt{\frac{C}{L}}=\frac{1}{2\zeta_p}$$

$$= \frac{\vert Y_C\vert}{G}=\frac{\omega_n C}{G}=\frac{C}{\sqrt{LC}G} =R\sqrt{\frac{C}{L}}=\frac{1}{2\zeta_p}$$ (196)

We note that $Q_p$ of the parallel RCL circuit is the reciprocal of $Q_s$ of the series RCL circuit:

$$\frac{1}{Q_s}=Q_p,\;\;\;\;\;\;\frac{1}{Q_p}=Q_s$$ (197)

When $\omega=\omega_n=1/\sqrt{LC}$, the voltage is $\dot{V}=\dot{I}/Y=\dot{I}/G=\dot{I}R$ and the currents through the three components are:

• $$\dot{I}_R=\dot{V}Y_R=\dot{V}G=\frac{\dot I}{G} G=\dot{I},$$ (198)

• $$\dot{I}_C=\dot{V} Y_C=\dot{I}R\;j\omega_n C=j\dot{I}R\frac{C}{\sqrt{LC}} =j \dot{I} R\;\sqrt{\frac{C}{L}}=jQ\dot{I}$$ (199)

• $$\dot{I}_L=\dot{V} Y_L=\dot{I}R\;\frac{1}{j\omega_n L} =-j\dot{I}R\frac{\sqrt{LC}}{L}=-j \dot{I} R\;\sqrt{\frac{C}{L}}=-jQ\dot{I}$$ (200)

We see that

• The current through $R$ is equal to the source current: $\dot{I}_R=\dot{I}$;
• The currents through $L$ and $C$ have the same magnitude, which is $Q_p$ times the input current: $\vert\dot{I}_L\vert=\vert\dot{I}_C\vert=Q_p\dot{I}$
• The currents through $L$ and $C$ have opposite phases: $\angle I_L=-\angle I_C$.

We see that $\dot{I}_L=-\dot{I}_C$, i.e., $I_L$ and $I_C$ have opposite directions, they form a loop current through $L$ and $C$.

The quality factor can also be used to judge whether a second order system is under, critically or over damped. Qualitatively, a greater $Q$ or a smaller $\zeta$ indicates that the system is energetic, active, and responsive, while on the other hand, a smaller $Q$ or a greater $\zeta$ indicates that the system is sluggish, inactive, and irresponsive.

$$\begin{array}{c\vert\vert c\vert\vert c} \hline \zeta<1 & Q>0... ...line \zeta>1 & Q<0.5 & \mbox{over damped} \\ \hline \end{array}$$ (201)

The concept of the quality factor $Q$ of a second order RCL circuit can be generalized to describe any second or higher order system, as the ratio between the energy stored in the system and the energy dissipated by the system:

$$Q=2\pi\frac{\mbox{Maximum energy stored}}{\mbox{Energy dissipated per cycle}}$$ (202)

In the case of the series RCL circuit, this is the ratio between the energy stored in $C$ and $L$ (proportional to $\omega L$ and $1/\omega C$) and the energy dissipated by $R$ (proportional to $R$) per period $T=1/f=2\pi/\omega$ at the natural frequency $\omega=\omega_n=1/\sqrt{LC}$. Consider the maximum energy stored in $L$:

$$W_L=\int_0^T i(t)\; v(t) dt=\int_0^T i(t) \,L \frac{di(t)}{dt} dt =L \int_0^{I_p} i \;di=\frac{1}{2}LI_p^2=LI^2_{rms}$$ (203)

and the maximum energy stored in $C$:

$$W_C=\int_0^T v(t)\; i(t) dt=\int_0^T v(t) \,C \frac{dv(t)}{dt} dt =C \int_0^{V_p} v \;dv=\frac{1}{2}CV_p^2=CV^2_{rms}$$ (204)

where $I_p=\sqrt{2}I_{rms}$ is the peak current through $L$, and $V_p=\sqrt{2}V_{rms}$ is the peak voltage across $C$.

At the natural frequency $\omega_n=1/\sqrt{LC}$, $\vert Z_C\vert=\vert Z_L\vert$, $\vert V_C\vert=\vert V_L\vert$, and the capacitor and the inductor store the same amount of energy:

$$W_L=LI^2_{rms}=L \left( \frac{V_{rms}}{\omega_nL}\right)^2 =L\frac{V^2_{rms}LC}{L^2}=CV^2_{rms}=W_C$$ (205)

The energy $W_L=W_C$ is converted back and forth between magnetic energy in $L$ and electrical energy in $C$. The energy dissipated in $R$ per cycle $T=2\pi/\omega_n=1/f_n$ is:

$$W_R=T\;P_R = T\;I^2_{rms} R$$ (206)

Substituting $W_L=W_C$ and $W_R$ into the definition of the quality factor, we get

$$Q=2\pi\frac{W_L}{W_R}=2\pi\frac{LI^2_{rms}}{TI^2_{rms}R } =2\pi f_n\frac{L}{R}=\frac{\omega_nL}{R}=\frac{1}{\omega_nCR}$$ (207)

which is the same as the $Q$ previously defined.

The quality factor $Q$ and the damping coefficient $\zeta$ are inversely related to each other:

$$Q_p=\frac{1}{2\zeta_p},\;\;\;\;\;\;\; \;\;\;\;\;\;\; Q_s=\frac{1}{2\zeta_s}$$ (208)

The phenomenon of resonance is of great importance in many physical systems such as mechanical structures and electrical circuits. One well known example of resonance causing damage in mechanical structures is the Broughton_Suspension_Bridge. On the other hand, resonance plays an important role in tuning circuits in radio and TV reception, as we will discuss later.