Kernelized Bayes classifier

The naive Bayes (maximum likelihood) classification is based on a quadratic decision function and is therefore unable to classify data that are not quadratically separable. However, as shown below, the Bayes method can be reformulated so that all data points appear in the form of an inner product, and the kernel method can be used to map the original space into a higher dimensional space in which all groups can be separated even though they are not quadratically separable in the original space.

Consider a binary Bayes classifier by which any sample ${\bf x}$ is classified into either of the two classes $C_+$ and $C_-$ depending on whether ${\bf x}$ is on the positive or negative side of the quadratic decision surface (Eq. (22)):

$$f({\bf x})={\bf x}^T{\bf W}{\bf x}+{\bf w}^T{\bf x}+w \left\{\begin{array}{ll}>0, & {\bf x}\in C_+\\ <0, & {\bf x}\in C_-\end{array}\right.$$ (172)

As show in Eq. (21), here

$${\bf W} = -\frac{1}{2}({\bf\Sigma}_+^{-1}-{\bf\Sigma}_-^{-1})$$

$${\bf w} = {\bf\Sigma}_+^{-1}{\bf m}_+-{\bf\Sigma}_-^{-1}{\bf m}_-$$

$$w = -\frac{1}{2}({\bf m}_+^T{\bf\Sigma}_+^{-1}{\bf m}_+ -{\bf m}_-^T{... ...{\vert{\bf\Sigma}_+\vert}{\vert{\bf\Sigma}_-\vert} +\log\,\frac{P(C_+)}{P(C_-)}$$ (173)

where ${\bf\Sigma}_+$ and ${\bf\Sigma}_-$ are respectively the covariance matrices of the samples in $C_+$ and $C_-$,

$${\bf m}_+=\frac{1}{N_+}\sum_{x\in C_+}{\bf x},\;\;\;\;\; {\bf m}_-=\frac{1}{N_-}\sum_{x\in C_-}{\bf x}$$ (174)

are their mean vectors, and $P_+=N_+/N$ and $P_-=N_-/N$ are their prior probabilities. Specially if ${\bf\Sigma}_+={\bf\Sigma}_-={\bf\Sigma}$ and therefore ${\bf W}={\bf0}$, the quadratic decision surface becomes a linear decision plane discribed by

$$f({\bf x})={\bf w}^T{\bf x}+w =\left[{\bf\Sigma}^{-1}({\bf m}_+-{\bf m}_-)\right]^T{\bf x}+w=0$$ (175)

in the same form as the decision equation for the support vector machine. An unlabeled sample ${\bf x}$ is classified into either of the two classes depending on on which side of a threshold $-w$ its projection onto the normal direction ${\bf w}$ of the decision plane lies.

As matrices ${\bf W}$, ${\bf\Sigma}_+^{-1}$, and ${\bf\Sigma}_-^{-1}$ are all symmetric, they can be written in the following eigendecomposition form:

$${\bf W}={\bf V}{\bf\Lambda}{\bf V}^T={\bf U}{\bf U}^T, \;\;\;\; {... ...\;\; {\bf\Sigma}_-^{-1}={\bf V}_-{\bf\Lambda}_-{\bf V}_-^T={\bf U}_-{\bf U}_-^T$$ (176)

where ${\bf U}={\bf V\Lambda}^{1/2},\;{\bf U}_+={\bf V}_+{\bf\Lambda}_+^{1/2}$ and ${\bf U}_-={\bf V}_-{\bf\Lambda}_-^{1/2}$. We can write vector ${\bf w}$ as:

$${\bf w}={\bf\Sigma}_+^{-1}{\bf m}_+-{\bf\Sigma}_-^{-1}{\bf m}_- =... ..._+}{\bf x}_+ -{\bf U}_-{\bf U}_-^T\frac{1}{N_-}\sum_{{\bf x}_-\in C_-}{\bf x}_-$$ (177)

Any unlabeled sample ${\bf x}$ can now be classified into either of the two classes based on its decision function:

$$f({\bf x}) = {\bf x}^T{\bf W}{\bf x}+{\bf w}^T{\bf x}+w$$

$$= {\bf x}^T{\bf UU}^T{\bf x} +\left(\frac{1}{N_+}\sum_{{\bf x}_+}{\... ...t(\frac{1}{N_-}\sum_{{\bf x}_-}{\bf x}_-^T{\bf U}_-{\bf U}_-^T\right){\bf x} +w$$

$$= {\bf z}^T{\bf z} +\frac{1}{N_+}\sum_{{\bf z}_{++}}\left({\bf z}_{... ...\right) -\frac{1}{N_-}\sum_{{\bf z}_{--}}\left({\bf z}_{--}^T{\bf z}_-\right)+w$$ (178)

where

$$\left\{\begin{array}{l}{\bf z}_{++}={\bf U}_+^T{\bf x}_+\;\;({\bf... ...{\bf z}_+={\bf U}_+^T{\bf x}\\ {\bf z}_-={\bf U}_-^T{\bf x} \end{array}\right.$$ (179)

As all data points appear in the form of an inner product, the kernel method can be used by replacing all inner products in the decision function by the corresponding kernel functions:

$$f({\bf x})=K({\bf z},{\bf z}) +\frac{1}{N_+}\sum_{{\bf z}_{++}}K(... ...}_+) -\frac{1}{N_-}\sum_{{\bf z}_{--}}K({\bf z}_{--},{\bf z}_-)+b =p({\bf x})+b$$ (180)

This is the decision function in the new higher dimensional space, where $p({\bf x})$ is defined as a function composed of all terms in $f({\bf x})$ except the last offset term $b$, which is to replace $w$ in the original space. To find this $b$, we first map all training samples into a 1-D space $x_n=p({\bf x}_n),\;(n=1,\cdots,N)$ and sort them together with their corresponding labelings $y_1,\cdots,y_N$, and then search through all $N-1$ possible ways to partition them into two groups indexed respectively by $1,\cdots,k$ and $k+1,\cdots,N$ to find the optimal $k$ corresponding to the maximum labeling consistency measured by

$$\bigg\vert\sum_{n=1}^k y_n\bigg\vert+\bigg\vert\sum_{n=k+1}^N y_n\bigg\vert, \;\;\;\;\;\;(k=1,\cdots,N-1)$$ (181)

The middle point $(x_k+x_{k+1})/2$ between $x_k$ and $x_{k+1}$ is used as the optimal threshold to separate the training samples into two classes in the 1-D space, i.e., the offset is $b=-(x_k+x_{k+1})/2$. Now the unlabeled point ${\bf x}$ can be classified into either of the two classes $C_+$ and $C_-$:

$$p({\bf x})+b\;\left\{\begin{array}{ll}>0, & {\bf x}\in C_+\\ <0, & {\bf x}\in C_-\end{array}\right.$$ (182)

In general, when all data points are kernel mapped to a higher dimensional space, the two classes can be more easily separated, even by a hyperplane based on the linear part of the decision function without the second order term. This allows the assumption that the two classes have the same covariance matrix so that ${\bf W}=-({\bf\Sigma}_+-{\bf\Sigma}_-)/2={\bf0}$ and the second order term is dropped. This is the justification for the following two special cases:

• If we approximate both ${\bf\Sigma}_+$ and ${\bf\Sigma}_-$ by their average ${\bf\Sigma}=({\bf\Sigma}_++{\bf\Sigma}_-)/2$, then ${\bf W}={\bf0}$ and the decision function of any ${\bf x}$ becomes
  

  $$f({\bf x}) = {\bf w}^T{\bf x}+w =\left[{\bf\Sigma}^{-1}({\bf m}_+-{\bf m}_-)\right]^T{\bf x}+w$$

  $$= \left[{\bf UU}^T\left(\frac{1}{N_+}\sum_{{\bf x}_+}{\bf x}_+ -\frac{1}{N_-}\sum_{{\bf x}_-}{\bf x}_-\right)\right]^T{\bf x}+w$$

  $$= \frac{1}{N_+}\sum_{{\bf x}_+}{\bf x}_+^T{\bf UU}^T{\bf x} -\frac{1}{N_-}\sum_{{\bf x}_-}{\bf x}_-^T{\bf UU}^T{\bf x}+w$$

  $$= \frac{1}{N_+}\sum_{{\bf z}_+}{\bf z}_+^T{\bf z} -\frac{1}{N_-}\sum_{{\bf z}_-}{\bf z}_-^T{\bf z}+w$$ (183)

  
  where ${\bf UU}^T={\bf\Sigma}^{-1}$, ${\bf z}_+={\bf U}^T{\bf x}_+$, ${\bf z}_-={\bf U}^T{\bf x}_-$, and ${\bf z}={\bf U}^T{\bf x}$. This decision function can be converted to the following if the kernel method is used:

  $$f({\bf x})=\frac{1}{N_+}\sum_{{\bf z}_+}K({\bf z}_+,{\bf z}) -\frac{1}{N_-}\sum_{{\bf z}_-}K({\bf z}_-,{\bf z})+b$$ (184)

• More specially, if ${\bf\Sigma}_+={\bf\Sigma}_-={\bf I}$, then the decision function above becomes
  

  $$f({\bf x}) = {\bf w}^T{\bf x}+w =\left( {\bf m}_+-{\bf m}_- \right)^T {\bf x}+w$$

  $$= \frac{1}{N_+}\sum_{{\bf x}_+}{\bf x}_+^T{\bf x} -\frac{1}{N_-}\sum_{{\bf x}_-}{\bf x}_-^T{\bf x}+w$$ (185)

  
  which can be converted to the following if the kernel method is used:

  $$f({\bf x})=\frac{1}{N_+}\sum_{{\bf x}_+}K({\bf x}_+,{\bf x}) -\frac{1}{N_-}\sum_{{\bf x}_-}K({\bf x}_-,{\bf x})+b$$ (186)

Note that if the kernel method is used to replace an inner product by a kernel function $K({\bf x},{\bf x}')=\phi({\bf x})^T\phi({\bf x}')$, we need to map all data points to $\phi({\bf x}_n),\;\;(n=1,\cdots,N)$ in the higher dimensional space, instead of only mapping their means $\phi({\bf m}_+)$ and $\phi({\bf m}_-)$, because the mapping of a sum is not equal to the sum of the mapped points if the kernel is not linear:

$$\phi({\bf m}_+-{\bf m}_-)\ne \phi({\bf m}_+)-\phi({\bf m}_-), \;\... ...n C_\pm}{\bf x}\right) \ne \frac{1}{n_\pm}\sum_{{\bf x}\in C_\pm} \phi({\bf x})$$ (187)

The three cases above are summarized below:

• Type I, Eq. (186)

  $$f({\bf x})=\frac{1}{N_+}\sum_{{\bf x}_+}K({\bf x}_+,{\bf x}) -\frac{1}{N_-}\sum_{{\bf x}_-}K({\bf x}_-,{\bf x})+b$$ (188)

• Type II, Eq. (183)

  $$f({\bf x})=\frac{1}{N_+}\sum_{{\bf z}_+}K({\bf z}_+,{\bf z}) -\frac{1}{N_-}\sum_{{\bf z}_-}K({\bf z}_-,{\bf z})+b$$ (189)

• Type III, Eq. (180)

  $$f({\bf x})={\bf z}^T{\bf z} +\frac{1}{N_+}\sum_{{\bf z}_{++}}K({\bf z}_{++},{\bf z}_+) -\frac{1}{N_-}\sum_{{\bf z}_{--}}K({\bf z}_{--},{\bf z}_-)+b$$ (190)

The Matlab code for the essential part of the algorithm is listed below. Given X and y for the data array composed of $N$ training vectors ${\bf X}=[{\bf x}_1,\cdots,{\bf x}_N]$ and their corresponding labelings ${\bf y}=[y_1,\cdots,y_N]$, the code carries out the training and then classifies any unlabeled data point into either of the two classes. Parameter type selects any one of the three different versions of the algorithm, and the function K(X,x) returns a 1-D array containing all $N$ kernel functions $K({\bf x}_i,{\bf x}),\;(i=1,\cdots,N)$ of the column vectors in ${\bf X}$ and vector ${\bf x}$.

    X=getData;
    [m n]=size(X);             
    X0=X(:,find(y>0));   n0=size(X0,2);     % separate C+ and C-
    X1=X(:,find(y<0));   n1=size(X1,2);   
    m0=mean(X0,2);    C0=cov(X0');          % calculate mean and covariance
    m1=mean(X1,2);    C1=cov(X1');    
    if type==1
        for i=1:n
            x(i)=sum(K(X0,X(:,i)))/n0-sum(K(X1,X(:,i)))/n1;
        end
    elseif type==2
        C=inv(C0+C1);   [V D]=eig(C);   U=(V*D^(1/2))';
        Z=U*X;  Z0=U*X0;   Z1=U*X1;
        for i=1:n
            x(i)=sum(K(Z0,Z(:,i)))/n0-sum(K(Z1,Z(:,i)))/n1;
        end
    elseif type==3
        C0=inv(C0);   C1=inv(C1);   W=-(C0-C1)/2;     
        [V D]=eig(W);     U=(V*D^(1/2)).';    Z=U*X;  
        [V0 D0]=eig(C0);  U0=(V0*D0^(1/2))';  Z0=U0*X;  Z00=U0*X0;
        [V1 D1]=eig(C1);  U1=(V1*D1^(1/2))';  Z1=U1*X;  Z11=U1*X1;
        for i=1:n
            x(i)=K(Z(:,i),Z(:,i))+sum(K(Z00,Z0(:,i)))/n0-sum(K(Z11,Z1(:,i)))/n1;
        end
    end
    [x I]=sort(x);   y=y(I);    % sort 1-D data together with their labelings
    smax=0;
    for i=1:n-1                 % find optimal threshold value b
        s=abs(sum(y(1:i)))+abs(sum(y(i+1:n)));
        if s>smax
            smax=s;  b=-(x(i)+x(i+1))/2;
        end
    end

Note that ${\bf W}=-({\bf\Sigma}_0^{-1}-{\bf\Sigma}_1^{-1})/2$ may be either positive or negative definite, and its eigenvalue matrix ${\bf D}$ may contain negative values and ${\bf D}^{1/2}$ may contain complex values. Given any unlabeled data point ${\bf x}$, the code below is carried out

    if type==1
        y(i)=sum(K(X0,x))/n0-sum(K(X1,x))/n1+b;
    elseif type==2
        Z=U*x;
        y(i)=sum(K(Z0,z))/n0-sum(K(Z1,z))/n1+b;
    elseif type==3
        z=U*x;    z0=U0*x;   z1=U1*x;
        y(i)=K(z,z)+sum(K(Z00,z0))/n0-sum(K(Z11,z1))/n1+b;
    end

to classify ${\bf x}$ into either $C_+$ if $y>0$, or $C_-$ if $y<0$.

In comparison with the SVM method, which requires solving a QP problem by certain iterative algorithm (either the interior point method or the SMO method), the kernel based Bayes method is closed-form and therefore extremely efficient computationally. Moreover, as shown in the examples below, this method is also highly effective as its classification results are comparable and offen more accurate than those of the SVM method.

We now show a few examples to test all three types of the kernel based Bayes method based on a set of simulated 2-D data. Both linear kernel and RBF kernel $K({\bf x},{\bf y})=\exp(-\gamma\vert\vert{\bf x}-{\bf y}\vert\vert)$. The value of the parameter $\gamma$ used in the examples is 5, but it can be fine tuned in a wide range (e.g., $1<\gamma<9$ to make proper trade-off between accuracy and avoiding overfitting. The performances of these method are also compared with the SVM method implemented by the Matlab function:

fitcsvm(X',y,'Standardize',true,'KernelFunction','linear','KernelScale','auto'))

Example 1: Based on some 2-D training datasets, four different binary classifiers are tested. The correct rates of each of the four methods are listed below, together with the corresponding partitionings of the 2-D space shown in the figures.

$$\begin{array}{l\vert\vert c\vert\vert c\vert c\vert c\vert c}... ...mbox{RBF} & 98.5\% & 100\% & 100\% & 100\%\\ \hline \end{array}$$ (191)

• Test 1: Two sets of data are generated based on the following mean vectors and covarience matrices:

  $${\bf m}_+=\left[\begin{array}{r}-1\\ 0\end{array}\right],\;\;\;\;... ...{\bf\Sigma}_- =3\times \left[\begin{array}{cc}1&0.5\\ 0.5&0.5\end{array}\right]$$ (192)

  The linear kernel is used for all methods. The kernel Bayes methods II and III achieve the best result $(94\%)$, slightly better than that of the standard SVM $(93\%)$. But the kernel Bayes method I performs poorly $(84.7\%)$, as it is based only on the means of the two classes without taking into consideration their covariances representing the distribution of the data points.

  

• Test 2: Two sets of data not linearly separable are classified by the four methods all based on the linear kernel. The kernel Bayes III achieves the best result $(96.5\%)$, due to its quadratic term in the decision function, the kernel Bayes I and II perform much more poorly, but still slightly better than the SVM method.

  

• Test 3: The same dataset as above is classified by the methods but now based on the RBF kernel. While the SVM performs performs reasonably well $(98.5\%)$, all three versions of the kernel Bayes method (with $\gamma=5$) achieve the perfect result with all points of the two classes completely separate. However, the partitioning of the space by the kernel Bayes III is highly fragmented, showing a sign of overfitting.

  

Example 2: The three datasets are generated using the Matlab code on this site. A parameter value $\gamma=5$ is used for the three versions of the kernel Bayes method.

$$\begin{array}{l\vert\vert c\vert\vert c\vert c\vert c\vert c}... ...x{RBF} & 96.0\% & 98.5\% & 95.5\% & 97.0\%\\ \hline \end{array}$$ (193)

• Test 1: Exclusive OR dataset, linear kernel

  As the data are not linearly separable, all methods performed poorly except kernelized Bayes Type III with a second order term in the decison function.

  

• Test 2: Exclusive OR dataset, RBF kernel

  All four methods performed very well, but all three variations of the kernelized Bayes method achieved higher correct rates than the SVM.

  

• Test 3: Cocentric ring dataset, RBF kernel

  

• Test 4: Multi-cluster dataset, RBF kernel

  

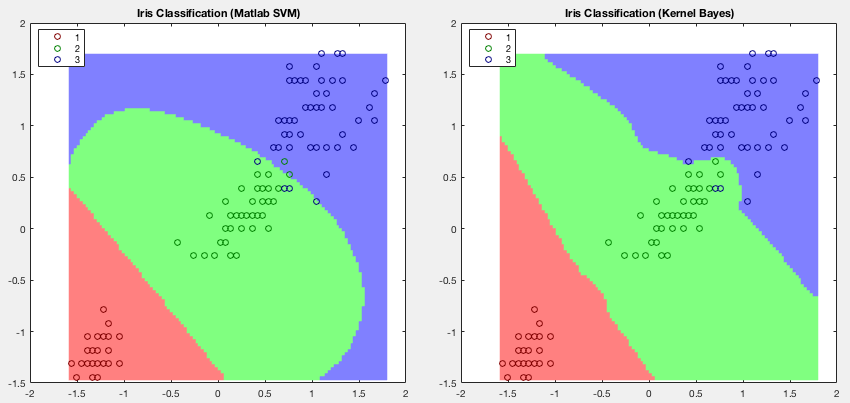
Example 3: The classification results of Fisher's iris data by the SVM method (Matlab function fitcsvm) and the kernel Bayes methods are shown below. This is an example used to illustrate the SVM method in the documentation of fitcsvm.

In this example only two (3rd and 4th) of the four features are used, with half of the samples used for training while the other half for testing. Note that the second class (setosa in green) and third class (versicolor in blue) not linearly separable can be better separated by the kernel Bayes method.