Next: Kernelized Bayes classifier Up: Support Vector machine Previous: Sequential Minimal Optimization (SMO)
CrammerSinger WestonWatkins WangXue Bredensteiner
The SVM method is inherently a binary classifier, but it can be
adapted to classification problems of more than two classes. In
the following, we consider a general K-class classifier based on a
training set
![${\bf X}=[{\bf x}_1,\cdots,{\bf x}_N]$](img9.svg)



We first consider two straight forward and imperical methods for multiclass classification based directly on binary SVM.
Any unlabeled 


This method converts a K-class problem (













if then then |
(159) |
We further consider another method for multiclass classifiction
by directly generalizing the binary SVM so that the decision
margin between any two of the 

 |
(160) |
 and
and  are determined during the
training set, any unlabeled point
are determined during the
training set, any unlabeled point  can be classified as
below:
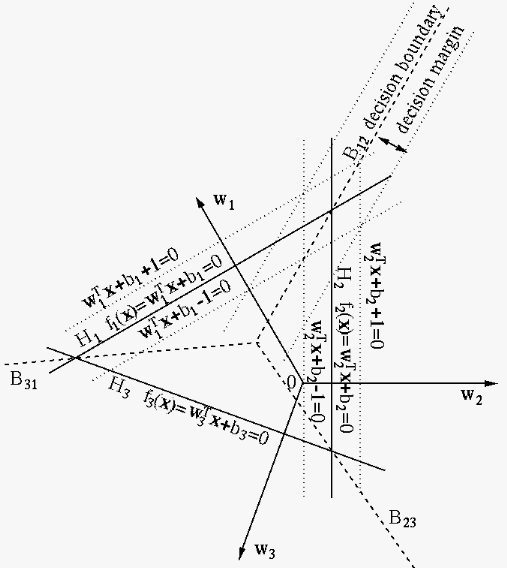
The figure below illustrates the classification of
can be classified as
below:
The figure below illustrates the classification of  classes
in
classes
in  dimensional feature space. Here each straight lines
dimensional feature space. Here each straight lines  (plane or hyperplane if
(plane or hyperplane if  ) is determined by equation
) is determined by equation
 , with
normal direction in
, with
normal direction in  and distance
and distance
 to the origin (same as in
Eq. (65)).
to the origin (same as in
Eq. (65)).
According to the classification rule in Eq. (161),
the 2-D feature space is partitioned into three regions each for
one of the 












 |
(162) |
 and
and  futher determine two straight
lines parallel to the decision boundary
futher determine two straight
lines parallel to the decision boundary  , defining the
decision margin between the support vectors of
, defining the
decision margin between the support vectors of  and
and  .
It can be seen that this decision margin is monotonically related
to both
.
It can be seen that this decision margin is monotonically related
to both
 and
and
 , which can
be maximized by minimizing both
, which can
be maximized by minimizing both
 and
and
 .
.
Now the multiclass classification problem can be formulated as
to find the parameters 









minimize: |
 |
||
subject to: |
 |
(163) |
Similar to Eq. (115) in soft margin SVM, the
contraints of the optimization problem above can be relaxed by
including in each contraint an extra error term

minimize: |
 |
||
subject to: |
 |
||
 |
|||
 |
(164) |
The Lagrangian function of this constrained optimization problem is
 |
 |
 |
|
 |
![$\displaystyle \sum_k\sum_n \alpha_{nk}\left[ ({\bf w}_{y_n}-{\bf w}_k)^T{\bf x}_n
+b_{y_n}-b_k-2+\xi_{nk}\right]-\sum_k\sum_n \beta_{nk}\xi_{nk}$](img635.svg) |
(165) |
 |
|||
 |
|||
 |
(166) |
 |
(167) |
 |
(168) |
 |
(169) |
 |
(170) |
![$\displaystyle {\bf W}=[{\bf w}_1,\cdots,{\bf w}_K]$](img642.svg) |
(171) |
 is classified to class
is classified to class  if
if
 .
.
The training of the classifier is to find all weight vectors in

////