Next: AdaBoost Up: ch9 Previous: K Nearest Neighbor and
The method of naive Bayes (NB) classification is a classical
supervised classification algorithm, which is first trained by a
training set of 
![${\bf X}=[{\bf x}_1,\cdots,{\bf x}_N]$](img9.svg)
![${\bf y}=[ y_1,\cdots,y_N]^T$](img10.svg)


 is the prior probability that any data sample
belongs to class
is the prior probability that any data sample
belongs to class  without observing its values, more briefly
denoted by
without observing its values, more briefly
denoted by  , which can be estimated by
where
, which can be estimated by
where  is the number of data samples in the training set
labeled to belong to class
is the number of data samples in the training set
labeled to belong to class  . This estimation is based on
the assumption that the training samples are evenly drawn from
the entire population, and are therefore a fair representation
of all
. This estimation is based on
the assumption that the training samples are evenly drawn from
the entire population, and are therefore a fair representation
of all  classes.
classes.
 is the likelihood for
any observed
is the likelihood for
any observed  to belong to class
to belong to class  , which is the
conditional probability of
, which is the
conditional probability of  given that
given that
 ,
assumed to be a
Gaussian
in
terms of the mean vector
,
assumed to be a
Gaussian
in
terms of the mean vector  and covariance matrix
and covariance matrix
 :
This assumption is based on the fact that the Gaussian distribution
has the maximum entropy (uncertainty) among all probability density
functions with the same covariance, i.e., it imposes the least amount
of unsupported constraint on the model for the dataset.
:
This assumption is based on the fact that the Gaussian distribution
has the maximum entropy (uncertainty) among all probability density
functions with the same covariance, i.e., it imposes the least amount
of unsupported constraint on the model for the dataset.
 is the joint probability of
is the joint probability of  and
and  :
:
 is the distribution of any data sample in the dataset,
independent of its classe identity, the weighted sum of all
likelihood
is the distribution of any data sample in the dataset,
independent of its classe identity, the weighted sum of all
likelihood
 for
for
 , i.e., the joint
probability
, i.e., the joint
probability
 marginalized over all
marginalized over all  classes:
classes:
 is the posterior probability that a data sample
is the posterior probability that a data sample
 belongs to class
belongs to class  based on the observed values in
based on the observed values in
![${\bf x}=[x_1,\cdots,x_d]^T$](img3.svg) .
.
Based on Bayes' theorem discussed above, the naive Bayes method
classifies an unlabeled data sample 

 is common to all
is common to all  classes (independent of
classes (independent of
 ), it plays no role in the relative comparison among the
), it plays no role in the relative comparison among the  classes, and can therefore be dropped, i.e.,
classes, and can therefore be dropped, i.e.,  is classified
to
is classified
to  with maximal
with maximal
 .
.
The naive Bayes classifier is an optimal classifier in the sense
that the classification error is minimum. To illustrate this,
consider an arbitrary boundary between two classes 






 |
 |
 |
|
 |
 |
||
 |
 |
(13) |
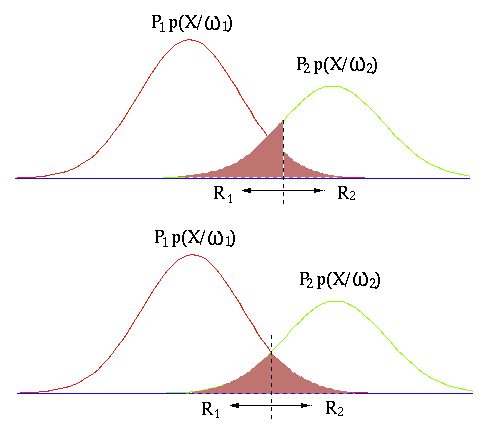
It is obvious that the Bayes classifier is indeed optimal, due to
the fact that its boundary



To find the likelihood function






 |
(14) |
Once both 


As the classification is based on the relative comparison of the
posterior

 |
 |
![$\displaystyle \log \left[ p({\bf x}\vert C_k) P_k/p({\bf x}) \right]
=\log p({\bf x}\vert C_k) +\log P_k-\log p({\bf x})$](img108.svg) |
|
 |
 |
(15) |
 and
and
 that are independent of the index
that are independent of the index  and therefore play no role in
the comparison above, we get the quadratic discriminant function:
and therefore play no role in
the comparison above, we get the quadratic discriminant function:
 |
(16) |
if then then |
(17) |
 |
(18) |
Geometrically, the feature space is partitioned into regions corresponding
to the 



 |
|||
 |
 |
(19) |
 |
(20) |
 is classified into either of
the two classes
is classified into either of
the two classes  and
and  based on whether it is on the positive
or negative side of the surface::
based on whether it is on the positive
or negative side of the surface::
We further consider several special cases:
 |
(23) |
 is zero, and we have
is zero, and we have
 |
(24) |
We can reconsider Example 2 in the previous section but now based on
the negative of the discriminant function above treated as a distance

 |
(25) |
 is classified into class
is classified into class  , while
, while  into
into  ,
as desired. The misclassification of
,
as desired. The misclassification of  to
to  by the Mahalanobis
distance, the first term, is corrected, due to the addition of the second
term
by the Mahalanobis
distance, the first term, is corrected, due to the addition of the second
term
 . The plot below shows the partitioning of the 1-D
space for the two classes
. The plot below shows the partitioning of the 1-D
space for the two classes  and
and  :
:
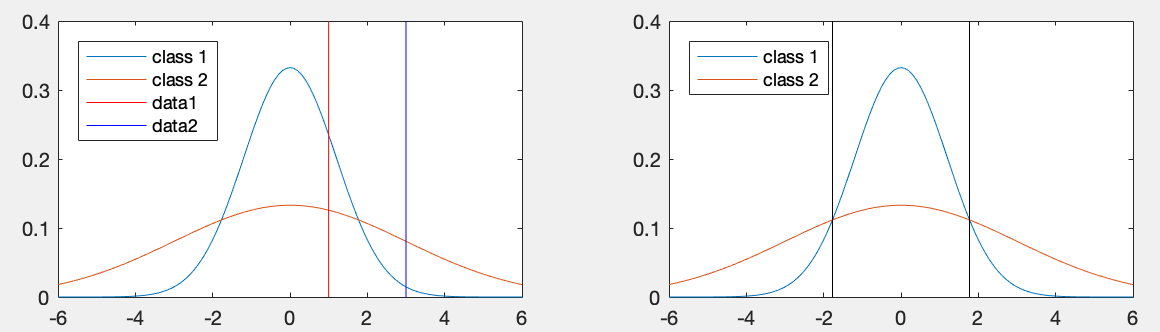
 ,
the discriminant function becomes:
,
the discriminant function becomes:
 |
(26) |
 are the same and the second term is dropped,
are the same and the second term is dropped,
 becomes the negative Mahalanobis distance.
becomes the negative Mahalanobis distance.
The boundary equation



 |
(27) |
 on both sides
of the equation are the same, it becomes a linear equation:
where
on both sides
of the equation are the same, it becomes a linear equation:
where
 |
(29) |
 |
(30) |
 and
and  and perpendicular to the straight line
and perpendicular to the straight line
 (the straight line
(the straight line
 rotated by matrix
rotated by matrix
 ).
).
![$\displaystyle {\bf\Sigma}_i={\bf\sigma}^2\,{\bf I}=diag[\sigma^2,\cdots,\sigma^2]$](img147.svg) |
(31) |
 and
and
 becomes
becomes
 |
(32) |
 has been dropped from the original
expression of
has been dropped from the original
expression of
 as it is now the same for all classes.
as it is now the same for all classes.
The boundary equation

 |
(33) |
 |
(34) |
 |
(35) |
 and
and  and perpendicular to the straight line passing through these
points.
and perpendicular to the straight line passing through these
points.
 ,
,
 becomes
becomes
 |
(36) |
 is equivalent to minimizing
is equivalent to minimizing
 .
.
The Matlab functions for training and testing are listed low:
function [M S P]=NBtraining(X,y) % naive Bayes training
[d N]=size(X); % dimensions of dataset
K=length(unique(y)); % number of classes
M=zeros(d,K); % mean vectors
S=zeros(d,d,K); % covariance matrices
P=zeros(1,K); % prior probabilities
for k=1:K
idx=find(y==k); % indices of samples in kth class
Xk=X(:,idx); % all samples in kth class
P(k)=length(idx)/N; % prior probability
M(:,k)=mean(Xk'); % mean vector of kth class
S(:,:,k)=cov(Xk'); % covariance matrix of kth class
end
end
function yhat=NBtesting(X,M,S,P) % naive Bayes testing
[d N]=size(X); % dimensions of dataset
K=length(P); % number of classes
for k=1:K
InvS(:,:,k)=inv(S(:,:,k)); % inverse of covariance matrix
Det(k)=det(S(:,:,k)); % determinant of covariance matrix
end
for n=1:N % for each of N samples
x=X(:,n);
dmax=-inf;
for k=1:K
xm=x-M(:,k);
d=-(xm'*InvS(:,:,k)*xm)/2;
d=d-log(Det(k))/2+log(P(k)); % discriminant function
if d>dmax
yhat(n)=k; % assign nth sample to kth class
dmax=d;
end
end
end
end
The classification result in terms of the estimated class identity





function [Cm er]=ConfusionMatrix(yhat,ytrain)
N=length(ytrain); % number of test samples
K=length(unique(ytrain)); % number of classes
Cm=zeros(K); % the confussion matrixxs
for n=1:N
i=ytrain(n);
j=yhat(n);
Cm(i,j)=Cm(i,j)+1;
end
er=1-sum(diag(Cm))/N; % error percentage
end
Example 1:
This example shows the classification of two cocentric classes with one
surrounding the other. They are separated by an ellipse with 9 out of
200 samples misclassified, i.e., the error rate of

![$\displaystyle \left[\begin{array}{rrr}
92 & 8 \\
1 & 99 \\
\end{array}\right]$](img158.svg) |
(37) |
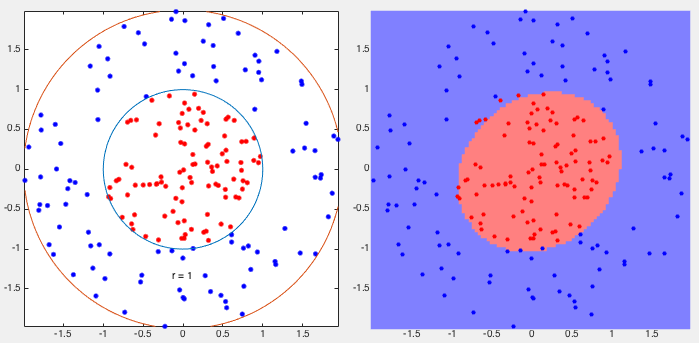
Example 2:
This example shows the classification of a 2-class exclusive-or (XOR)
data set with significant overlap, in terms of the confusion matrix and
the error rate of

![$\displaystyle \left[\begin{array}{rrr}
175 & 25 \\
36 & 164 \\
\end{array}\right]$](img160.svg) |
(38) |
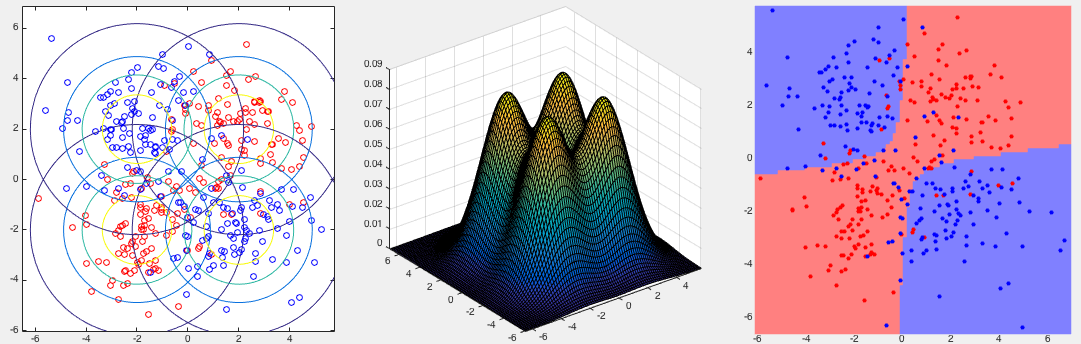
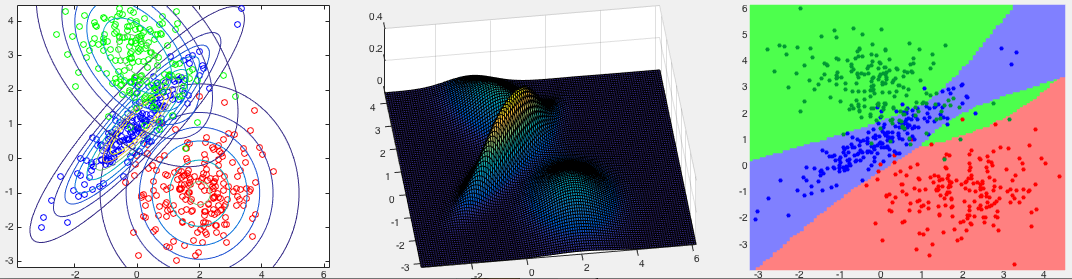
Example 3:
The first two panels in the figure below show three classes in the 2-D
space, while the third one shows the partitioning of the space corresponding
to the three classes. Note that the boundaries between the classes are all
quadratic. The confusion matrix of the classification result is shown below,
with the error rate

![$\displaystyle \left[\begin{array}{rrr}
196 & 3 & 1 \\
0 & 191 & 9 \\
3 & 33 & 164 \\
\end{array}\right]$](img162.svg) |
(39) |
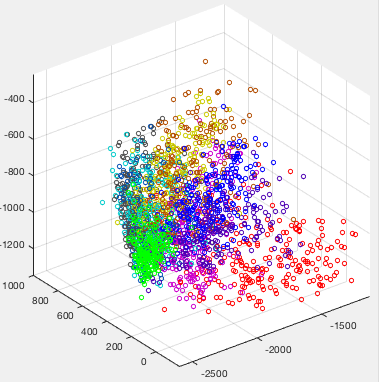
Example 4
The figure below shows some sub-samples of ten sets digits from 0 to 9, each is hand-written 224 times by different students. Each hand-written digit is represented as an 16 by 16 image containing 256 pixels, treated as a 256 dimensional vector.

The dataset can be visualized by applying the KLT transform to map all data points in the 256-D space into a 3-D space spanned by the three eigenvectors corresponding to the three greatest eigenvalues of the covariance matrix of the dataset, as shown below:
The naive Bayes classifier is applied to the dataset of handwritten
digits from 0 to 9, of which each data sample is a 256-dimensional
vector composed of



We note that the 256-dimensional covariance matrix


The classifier is trained on half of
the dataset of 1120 randomly selected samples and then tested on the
remaining 1120 samples. The classification results are given below
in terms of the confusion matrices of the traing samples (left) and
the testing samples (right). All 1120 training samples are correctly
classfied, while out of the remaining 1120 test samples, 198 are
misclassified (
![$\displaystyle \left[ \begin{array}{rrrrrrrrrr}
107 & 0 & 0 & 0 & 0 & 0 & 0 & 0 ...
... 18 & 109 & 9 \\
0 & 3 & 0 & 0 & 2 & 0 & 0 & 2 & 0 & 90 \\
\end{array}\right]$](img167.svg) |
(40) |