The Gaussian process regression (GPR) is yet another
regression method that fits a regression function
 to the data samples in the given training set. Different from
all previously considered algorithms that treat
to the data samples in the given training set. Different from
all previously considered algorithms that treat
 as a deterministic function with an explicitly specified form,
the GPR treats the regression function
as a deterministic function with an explicitly specified form,
the GPR treats the regression function
 as a
stochastic process called Gaussian process (GP), i.e.,
the function value
as a
stochastic process called Gaussian process (GP), i.e.,
the function value
 at any point
at any point  is
assumed to be a random variable with a Gaussian distribution.
is
assumed to be a random variable with a Gaussian distribution.
The joint probability distribution of the vector function
![${\bf f}({\bf X})=[f({\bf x}_1),\dots,f({\bf x}_N)]^T$](img1162.svg) for
all
for
all  i.i.d. samples in the training set
i.i.d. samples in the training set  is also
Gaussian:
is also
Gaussian:
 |
(251) |
where, for convenience and without loss of generality, we have
assumed a zero mean
 . The ultimate goal is
to estimate the regression function
. The ultimate goal is
to estimate the regression function
 in terms of
its Gaussian pdf
in terms of
its Gaussian pdf
 .
.
We also assume
 as the
labeling of
as the
labeling of  in the training set is contaminatd by
noise
in the training set is contaminatd by
noise  , with a zero-mean normal pdf
, with a zero-mean normal pdf
 |
(252) |
where the diagonal covariance matrix
 is
based on the assumption that all components of
is
based on the assumption that all components of  are
independent of each other. We further assume noise
are
independent of each other. We further assume noise  is
independent of
is
independent of  with
with
 .
Now
.
Now
 , as
the sum of two zero-mean Gaussian variables, is also a zero
mean Gaussian process.
, as
the sum of two zero-mean Gaussian variables, is also a zero
mean Gaussian process.
The unknown covariance matrix
 can be
constructed based on the desired smoothness of the regression
function
can be
constructed based on the desired smoothness of the regression
function
 , in the sense that any two function
values
, in the sense that any two function
values
 and
and
 are likely to be
more correlated if the distance
are likely to be
more correlated if the distance
 between the two corresponding points is small, but less so
if the distance is large. Such a covariance can be modeled
by a squared exponential (SE) kernel function:
between the two corresponding points is small, but less so
if the distance is large. Such a covariance can be modeled
by a squared exponential (SE) kernel function:
 |
(253) |
where
 is a
kernel function
of
is a
kernel function
of  and
and  . This SE function may take
any value between 1 when
. This SE function may take
any value between 1 when
 and
and
 are maximally correlated, and 0
when
are maximally correlated, and 0
when
 and
and
 and
and
 are minimally correlated. We therefore see
that the SE so constructed mimics the covariance of a smooth
function
are minimally correlated. We therefore see
that the SE so constructed mimics the covariance of a smooth
function
 .
.
The smoothness of the function
 plays a very
important role as it determines whether the function
overfits or underfits the sample points in the training
data. If the function is not smooth enough, it may overfit
as it may overly affected by some noisy samples; on the
other hand, if the function is too smooth, it may underfit
as it may not follow the training samples closely enough.
plays a very
important role as it determines whether the function
overfits or underfits the sample points in the training
data. If the function is not smooth enough, it may overfit
as it may overly affected by some noisy samples; on the
other hand, if the function is too smooth, it may underfit
as it may not follow the training samples closely enough.
The smoothness of the regression function can be controlled
by the hyperparameter  in Eq. (253).
Consider two extreme cases. If
in Eq. (253).
Consider two extreme cases. If
 , i.e.,
the value of the SE approaches 1, then
, i.e.,
the value of the SE approaches 1, then
 and
and
 are highly correlated and
are highly correlated and
 is
smooth; on the other hand, if
is
smooth; on the other hand, if
 , i.e., SE
approaches 0, then
, i.e., SE
approaches 0, then
 and
and
 are
not correlated and
are
not correlated and
 is not smooth. Therefore
by adjusting the value of
is not smooth. Therefore
by adjusting the value of  , a proper tradeoff between
overfitting and underfitting can be made.
, a proper tradeoff between
overfitting and underfitting can be made.
Given the covariance
 of
function values at two different sample points
of
function values at two different sample points  and
and
 , we can represent the covariance matrix of the prior
, we can represent the covariance matrix of the prior
 as
as
![$\displaystyle {\bf\Sigma}_f=Cov({\bf f},{\bf f})
=\left[\begin{array}{ccc}
k({\...
...cdots & k({\bf x}_N,\,{\bf x}_N)
\end{array}\right]
=K({\bf X},{\bf X})={\bf K}$](img1185.svg) |
(254) |
Note that the value of all diagonal components are the same
 ; and the greater the
distance
; and the greater the
distance
 , the farther away the component
, the farther away the component
 is from the diagonal, and the lower value
it takes.
is from the diagonal, and the lower value
it takes.
Once the conditional probability
 is estimated
based on the training set
is estimated
based on the training set
![${\bf X}=[{\bf x},\cdots,{\bf x}_N]$](img1189.svg) , we
can get the mean and covariance of
, we
can get the mean and covariance of
 of a test dataset
of a test dataset
![${\bf X}_*=[{\bf x}_{1*},\cdots,{\bf x}_{M*}]$](img597.svg) containing
containing  unlabeled test samples. As both
unlabeled test samples. As both  and
and
 are the same zero-mean Gaussian process, their joint
distribution (given
are the same zero-mean Gaussian process, their joint
distribution (given  as well as
as well as  ) is also a
zero-mean Gaussian:
) is also a
zero-mean Gaussian:
where
 |
(256) |
can all be constructed based on the SE function, same as how
 is constructed.
is constructed.
Having found the joint pdf
 of both
of both  and
and  in Eq. (255), we
can further find the conditional distribution
in Eq. (255), we
can further find the conditional distribution
 of
of  given
given
 (as well as
(as well as  and
and  ), based on the
properties of the Gaussian distributions discussed in the
Appendices:
), based on the
properties of the Gaussian distributions discussed in the
Appendices:
 |
(257) |
with the mean and covariance
 |
(258) |
Similarly, we can also find the joint distribution of  and
and
 , both of which are zero-mean Gaussian:
, both of which are zero-mean Gaussian:
![$\displaystyle p({\bf y},{\bf f}_*\vert{\bf X},{\bf X}_*)={\cal N}\left(
\left[\...
...igma}_{yf_*}\\
{\bf\Sigma}_{f_*y} & {\bf\Sigma}_{f_*}\end{array}\right]\right)$](img1201.svg) |
(259) |
where
where
 .
Now we have
.
Now we have
![$\displaystyle Cov\left[ \begin{array}{c} {\bf y} \\ {\bf f}_* \end{array} \righ...
...sigma_n^2{\bf I} & {\bf K}_* \\
{\bf K}^T_* & {\bf K}_{**} \end{array} \right]$](img1209.svg) |
(261) |
We can now further get the desired conditional distribution of
 given
given  as well as the training set
as well as the training set
 :
:
 |
(262) |
with the mean and covariance
 |
(263) |
We see that these expressions are the same as those in
Eq. (184) previously obtained by Bayesian
linear regression, i.e., the same results can be derived by
two very different methods.
In the special noise-free case of
 (with zero mean and zero covariance
(with zero mean and zero covariance
 ), we have
), we have
 , and the mean and covariance
in Eq. (263) become the same as Eq. (258),
and Eqs. (262) and (257) become
the same:
, and the mean and covariance
in Eq. (263) become the same as Eq. (258),
and Eqs. (262) and (257) become
the same:
 |
(264) |
The Matlab code below for the Gaussian process regression
algorithm, takes the training set
 ,
the test samples in
,
the test samples in  , and the variance
, and the variance
 of the noise as the input, and generates as the output the
posterior
of the noise as the input, and generates as the output the
posterior
 , in terms of its
mean as the GPR regression function, and its covariance matrix,
of which the variances on the diagonal represent the confidence
or certainty of the regression.
, in terms of its
mean as the GPR regression function, and its covariance matrix,
of which the variances on the diagonal represent the confidence
or certainty of the regression.
function [fmean fcov]=GPR(X,y,Xstar,sigmaN) % given training set D={X,y}, test sample Xstar
% find regression function fmean and covariance
Sy=Kernel(X,X)+sigmaN^2*eye(length(X)); % Covariance of training samples
Syf=Kernel(X,Xstar); % Covariance of training and test samples
Sf=Kernel(Xstar,Xstar); % Covariance of test samples
fmean=Syf'*inv(Sy)*y; % mean of posterior as the regression function
fcov=Sf-Syf'*inv(Sy)*Syf; % covariance of posterior
end
The follwoing code is for a function that generates the squared
exponential kernel matrix based on two sets of data samples
in X1 and X2:
function K=Kernel(X1,X2)
a=1; % parameter that controls smoothness of f(x)
m=length(X1);
n=length(X2);
K=zeros(m,n);
for i=1:m
for j=1:n
d=norm(X1(:,i)-X2(:,j));
K(i,j)=exp(-(d/a)^2);
end
end
end
Example:
A sinusoidal function
 contaminated by
Gaussian noise
contaminated by
Gaussian noise  with
with
 is sampled at
is sampled at  random positions over the duration of the
function
random positions over the duration of the
function  . These samples form the training dataset
. These samples form the training dataset
 .
.
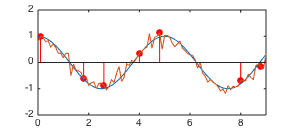
Then the method of GPR is used to estimate the mean and variance of
 at 91 test points
at 91 test points  , evenly distributed over the
duration of the function between the limits
, evenly distributed over the
duration of the function between the limits  and
and  ,
,
The 8 panels of the figure below show the estimated mean ![$\E[f_*]$](img1228.svg) , and
the variance
, and
the variance
![$\pm \Var[f_*]$](img1229.svg) , both above and below the mean, to form a
region of uncertainty of the estimates. The wider the region, the more
uncertain the results are (less confidence).
, both above and below the mean, to form a
region of uncertainty of the estimates. The wider the region, the more
uncertain the results are (less confidence).
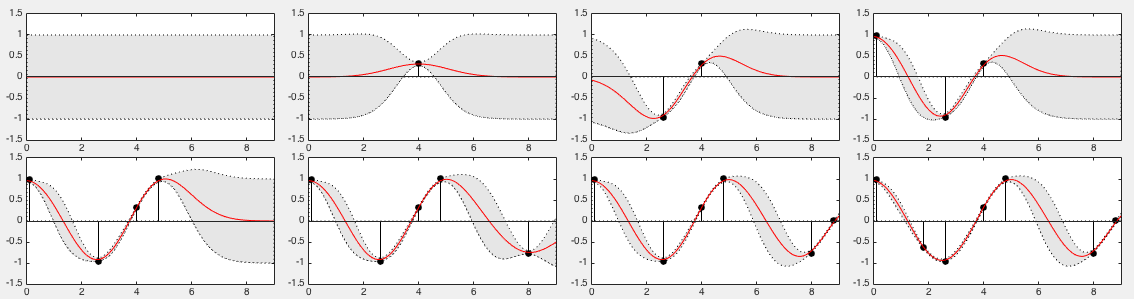
The top left panel represents the prior probability
 of the estimated model output
of the estimated model output
 at point
at point  with
no knowledge based on the training set
with
no knowledge based on the training set  (
( training
samples), which is assumed to have zero-mean
training
samples), which is assumed to have zero-mean ![$\E[f_*]=0$](img1234.svg) and unity
variance
and unity
variance
![$\Var[f(x_*)]=k(x_*, x_*)=1$](img1235.svg) . The subsequent seven panels
show the mean and variance of the posterior
. The subsequent seven panels
show the mean and variance of the posterior
 based on
based on
 training
samples in the training set
training
samples in the training set . Note that wherever a training
sample
. Note that wherever a training
sample  becomes available, the estimated mean
becomes available, the estimated mean
 is
modified to be close to the true function value
is
modified to be close to the true function value  , and the
variance of the posterior around
, and the
variance of the posterior around  is reduced, indicating the
uncertainty of the estimate is reduced, or the confidence is much
increased. When all
is reduced, indicating the
uncertainty of the estimate is reduced, or the confidence is much
increased. When all  training samples are used, the general
shape of the original function is reasonably reconstructed.
training samples are used, the general
shape of the original function is reasonably reconstructed.
The 8 panels in the figure below show 12 sample curves drawn from
each posterior
 . They can be treated as
different interpolations for the
. They can be treated as
different interpolations for the  observed samples in training
set
observed samples in training
set  , and any of them can be used to predict the outputs
, and any of them can be used to predict the outputs
 at any input points
at any input points  . The mean of these samples shown
as the red curve is simply the same as
. The mean of these samples shown
as the red curve is simply the same as ![$\E[f_*]$](img1228.svg) shown in the
previous figure.
shown in the
previous figure.
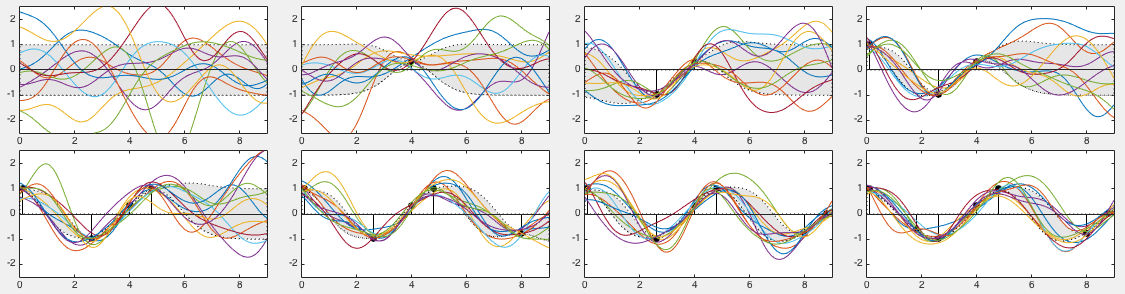
We see that wherever a training sample  is available at
is available at  ,
the variance and thereby the width of the region of uncertainty is
reduced, and correspondingly the sample curves in the neighborhood
of
,
the variance and thereby the width of the region of uncertainty is
reduced, and correspondingly the sample curves in the neighborhood
of  are more tightly distributed. Specifically, we see that the
sample curves drawn from the prior in the top left panel are very
loosely distributed, while those samples drawn from the posterior
obtained based on all
are more tightly distributed. Specifically, we see that the
sample curves drawn from the prior in the top left panel are very
loosely distributed, while those samples drawn from the posterior
obtained based on all  training points in the bottom right panel
are relatively tightly distributed. In particular, note that due
to lack of training data in the interval
training points in the bottom right panel
are relatively tightly distributed. In particular, note that due
to lack of training data in the interval  , the region of
uncertainty is significantly wider than else where, and the sample
curves are much more loosely located.
, the region of
uncertainty is significantly wider than else where, and the sample
curves are much more loosely located.
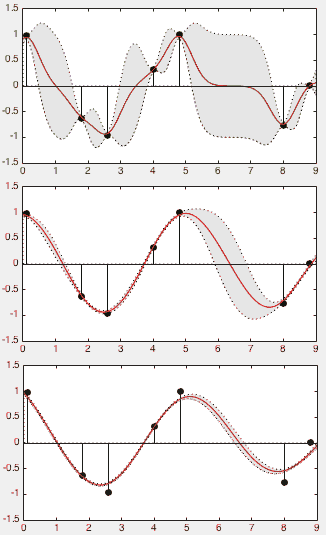
The parameter  of the kernel function plays an important
role in the GPR results, as shown in the three panels in the figure
below, corresponding respectively to
of the kernel function plays an important
role in the GPR results, as shown in the three panels in the figure
below, corresponding respectively to  values of 0.5, 1.5, and 3.0.
When
values of 0.5, 1.5, and 3.0.
When  is too small (top panel), the model may overfit the data,
as the regression function fits the training samples well but it not
smooth and it does not interpolate regions between the training
samples well (with large variance); one the other hand, when
is too small (top panel), the model may overfit the data,
as the regression function fits the training samples well but it not
smooth and it does not interpolate regions between the training
samples well (with large variance); one the other hand, when  is too large (bottom panel), the model may underfit the data, as
the regression curve is smooth, but it does not fit the training
samples well. We therefore see that we need to choose the value
of
is too large (bottom panel), the model may underfit the data, as
the regression curve is smooth, but it does not fit the training
samples well. We therefore see that we need to choose the value
of  carefully for a proper tradeoff between overfitting and
underfitting (middle panel).
carefully for a proper tradeoff between overfitting and
underfitting (middle panel).





![${\bf f}({\bf X})=[f({\bf x}_1),\dots,f({\bf x}_N)]^T$](img1162.svg)



 . The ultimate goal is
to estimate the regression function
. The ultimate goal is
to estimate the regression function
 in terms of
its Gaussian pdf
in terms of
its Gaussian pdf
 .
.




 is
based on the assumption that all components of
is
based on the assumption that all components of  are
independent of each other. We further assume noise
are
independent of each other. We further assume noise  is
independent of
is
independent of  with
with
 .
Now
.
Now
 , as
the sum of two zero-mean Gaussian variables, is also a zero
mean Gaussian process.
, as
the sum of two zero-mean Gaussian variables, is also a zero
mean Gaussian process.





 is a
kernel function
of
is a
kernel function
of  and
and  . This SE function may take
any value between 1 when
. This SE function may take
any value between 1 when
 and
and
 are maximally correlated, and 0
when
are maximally correlated, and 0
when
 and
and
 and
and
 are minimally correlated. We therefore see
that the SE so constructed mimics the covariance of a smooth
function
are minimally correlated. We therefore see
that the SE so constructed mimics the covariance of a smooth
function
 .
.















 ; and the greater the
distance
; and the greater the
distance
 , the farther away the component
, the farther away the component
 is from the diagonal, and the lower value
it takes.
is from the diagonal, and the lower value
it takes.

![${\bf X}=[{\bf x},\cdots,{\bf x}_N]$](img1189.svg)

![${\bf X}_*=[{\bf x}_{1*},\cdots,{\bf x}_{M*}]$](img597.svg)






 is constructed.
is constructed.










![$\displaystyle p({\bf y},{\bf f}_*\vert{\bf X},{\bf X}_*)={\cal N}\left(
\left[\...
...igma}_{yf_*}\\
{\bf\Sigma}_{f_*y} & {\bf\Sigma}_{f_*}\end{array}\right]\right)$](img1201.svg)










 .
Now we have
.
Now we have
![$\displaystyle Cov\left[ \begin{array}{c} {\bf y} \\ {\bf f}_* \end{array} \righ...
...sigma_n^2{\bf I} & {\bf K}_* \\
{\bf K}^T_* & {\bf K}_{**} \end{array} \right]$](img1209.svg)
 given
given  as well as the training set
as well as the training set
 :
with the mean and covariance
We see that these expressions are the same as those in
Eq. (184) previously obtained by Bayesian
linear regression, i.e., the same results can be derived by
two very different methods.
:
with the mean and covariance
We see that these expressions are the same as those in
Eq. (184) previously obtained by Bayesian
linear regression, i.e., the same results can be derived by
two very different methods.



















![$\E[f_*]$](img1228.svg)
![$\pm \Var[f_*]$](img1229.svg)






![$\E[f_*]=0$](img1234.svg)
![$\Var[f(x_*)]=k(x_*, x_*)=1$](img1235.svg)













![$\E[f_*]$](img1228.svg)











