As we have seen above, Newton's methods can be used to solve both
nonlinear systems to find roots of a set of simultaneous equations,
and optimization problems to minimize a scalar-valued objective function
based on the iterations of the same form. Specifically,
If the Jacobian
 or the Hessian matrix
or the Hessian matrix
 is not available, or if it is too computationally costly to calculate
its inverse (with complexity
is not available, or if it is too computationally costly to calculate
its inverse (with complexity  ), the quasi-Newton methods can be
used to approximate the Hessian matrix or its inverse based only on
the first order derivative, the gradient
), the quasi-Newton methods can be
used to approximate the Hessian matrix or its inverse based only on
the first order derivative, the gradient  of
of
 (with complexity
(with complexity  ), similar to
Broyden's method
previously
considered.
), similar to
Broyden's method
previously
considered.
In the following, we consider the minimization of a function
 .
Its Taylor expansion around point
.
Its Taylor expansion around point
 is
is
 |
(80) |
Taking derivetive with respect to  , we get
, we get
 |
(81) |
Evaluating at
 , we have
, we have
 ,
and the above can be written as
,
and the above can be written as
where matrix  is the secant approximation of the Hessian
matrix
is the secant approximation of the Hessian
matrix  , and the last eqality is called the
secant equation. For convenience, we further define:
, and the last eqality is called the
secant equation. For convenience, we further define:
 |
(83) |
so that the equation above can be written as
 or or |
(84) |
This is the quasi-Newton equation, which is the
secant condition that must be satisfied by matrix
 , or its inverse
, or its inverse
 , in any of the
quasi-Newton algorithms, all taking the follow general steps:
, in any of the
quasi-Newton algorithms, all taking the follow general steps:
- Initialize
 and
and  , set
, set  ;
;
- Compute gradient
 and the search direction
and the search direction
 ;
;
- Get
 with step
size
with step
size  satisfying the
Wolfe conditions.
satisfying the
Wolfe conditions.
- update
 or
or
 ,
that satisfies the quasi-Newton equation;
,
that satisfies the quasi-Newton equation;
- If termination condition is not satisfied,
 , go back
to second step.
, go back
to second step.
For this iteration to converge to a local minimum of
 ,
,
 must be positive definite matrix, same as the Hessian
matrix
must be positive definite matrix, same as the Hessian
matrix  it approximates. Specially, if
it approximates. Specially, if
 ,
then
,
then
 , the algorithm becomes the gradient
descent method; also, if
, the algorithm becomes the gradient
descent method; also, if
 is the Hessian matrix,
then the algorithm becomes the Newton's method.
is the Hessian matrix,
then the algorithm becomes the Newton's method.
In a quasi-Newton method, we can choose to update either  or its inverse
or its inverse
 based on one of the two forms of
the quasi-Newton equation. We note that there is a dual relationship
between the two ways to update, i.e., by swapping
based on one of the two forms of
the quasi-Newton equation. We note that there is a dual relationship
between the two ways to update, i.e., by swapping  and
and
 , an update formula for
, an update formula for  can be directly
applied to its inverse and vice versa.
can be directly
applied to its inverse and vice versa.
- The Symmetric Rank 1 (SR1) Algorithm
Here matrix  is updated by an additional term:
is updated by an additional term:
 |
(85) |
where  a vector and
a vector and
 is a matrix of rank 1.
Imposing the secant condition, we get
is a matrix of rank 1.
Imposing the secant condition, we get
 i.e., i.e., |
(86) |
This equation indicats  is in the same direction as
is in the same direction as
 , and can therefore
be written as
, and can therefore
be written as
 . Substituting this back we get
. Substituting this back we get
 |
(87) |
Solving this we get
 ,
,
 |
(88) |
and the iteration of  becomes
becomes
 |
(89) |
Applying the
Sherman-Morrison formula,
we can further get the inverse
 :
:
We note that this equation is dual to the previous one, and it
can also be obtained based on the duality between the secant
conditions for  and
and
 . Specifically,
same as above, we impose the secant condition for the inverse
. Specifically,
same as above, we impose the secant condition for the inverse
 of the following form
of the following form
 |
(91) |
and get
 |
(92) |
Then by repeating the same process above, we get the same update
formula for
 .
.
This is the formula for directly updating
 .
For the iteration to converge to a local minimum, matrix
.
For the iteration to converge to a local minimum, matrix
 needs to be positive definite as well as
needs to be positive definite as well as
 , we therefore require
, we therefore require
 |
(93) |
It may be difficult to maintain this requirement through out the
iteration. This problem can be avoided in the following DFP and
BFGS methods.
- The BFGS (Broyden-Fletcher-Goldfarb-Shanno) algorithm
This is a rank 2 algorithm in which matrix  is updated
by two rank-1 terms:
is updated
by two rank-1 terms:
 |
(94) |
Imposing the secant condition for  , we get
, we get
 |
(95) |
or
 |
(96) |
which can be satisfied if we let
 |
(97) |
Substituting these into
 we get
we get
 |
(98) |
Given this update formula for  , we can further find its
inverse
, we can further find its
inverse
 and then the search direction
and then the search direction
 .
.
Alternatively, given  , we can further derive an update
formula directly for the inverse matrix
, we can further derive an update
formula directly for the inverse matrix
 , so that
the search direction
, so that
the search direction  can be obtained without carrying
out the inversion computation. Specifically, we first define
can be obtained without carrying
out the inversion computation. Specifically, we first define
![${\bf U}=[{\bf u}_1\;{\bf u}_2]$](img438.svg) and
and
![${\bf V}=[{\bf v}_1\;{\bf v}_2]$](img439.svg) ,
where
,
where
 |
(99) |
so that the expression above can be written as:
 |
(100) |
and then apply the
Sherman-Morrison formula,
to get:
where we have defined
![$\displaystyle {\bf C}=\left[\begin{array}{cc}c_{11} & c_{12}\\ c_{21} & c_{22}\...
...1}{\bf U}
={\bf I}+[{\bf v}_1\;{\bf v}_2]^T{\bf B}^{-1}_n[{\bf u}_1\;{\bf u}_2]$](img444.svg) |
(102) |
with
 |
(103) |
 |
(104) |
 |
(105) |
 |
(106) |
![$\displaystyle {\bf C}=\left[\begin{array}{cc}c_{11} & c_{12}\\ -c_{12} & 0\end{...
...t[\begin{array}{cc}0 & -1/c_{12}\\ 1/c_{12} & c_{11}/c_{12}^2\end{array}\right]$](img449.svg) |
(107) |
Substituting this
 into the expression for
into the expression for
 , we get:
, we get:
where
 |
(109) |
 |
(110) |
Substituting these three terms back into Eq. (108),
we get the update formula for
 :
:
 |
(112) |
In summary,
 can be found by either Eq.
(98) for
can be found by either Eq.
(98) for
 followed by an additional
inversion operation, or Eq. (112) directly for
followed by an additional
inversion operation, or Eq. (112) directly for
 . The results obtained by these methods are
equivalent.
. The results obtained by these methods are
equivalent.
- The DFP (Davidon-Fletcher-Powell) Algorithm
Same as the BFGS algorithm, the DFP algorithm is also a rank 2
algorithm, where instead of  , the inverse matrix
, the inverse matrix
 is updated by two rank-1 terms:
is updated by two rank-1 terms:
 |
(113) |
where  and
and  are real scalars,
are real scalars,  and
and  are vectors. Imposing the secant condition for the inverse of
are vectors. Imposing the secant condition for the inverse of
 , we get
, we get
 |
(114) |
or
 |
(115) |
which can be satisfied if we let
 |
(116) |
Substituting these into
 we get
we get
 |
(117) |
Following the same procedure used for the BFGS method, we can also
obtain the update formular of matrix  for the DFP method:
for the DFP method:
 |
(118) |
We note that Eqs. (117) and (98) form
a duality pair, and Eqs. (118) and (112)
form another duality pair. In other words, the BFGS and FDP methods
are dual of each other.
In both the DFP and BFGS methods, matrix
 , as
well as
, as
well as  , must be positive definite, i.e.,
, must be positive definite, i.e.,
 must hold for any
must hold for any
 .
We now prove that this requirement is satisfied if the curvature
condition of the Wolfe conditions
is satisfied:
.
We now prove that this requirement is satisfied if the curvature
condition of the Wolfe conditions
is satisfied:
 i.e. i.e. |
(119) |
Replacing the search direction  by
by
 , we get:
, we get:
 |
(120) |
We also have
 |
(121) |
Substracting the first equation from the second, we get
 |
(122) |
The last inequality is due to the fact that
 and
and  . We therefore have
. We therefore have
 |
(123) |
Given
 , we can further prove by
induction that both
, we can further prove by
induction that both
 and
and
 based repectively on the update formulae in Eqs.
(98) and (117) are positive
definite. We first assume
based repectively on the update formulae in Eqs.
(98) and (117) are positive
definite. We first assume  and
and  are both
positive definite, and express
are both
positive definite, and express  in terms of its
Cholesky decomposition,
in terms of its
Cholesky decomposition,
 . We further
define
. We further
define
 ,
,
 ,
and get
,
and get
 |
(124) |
Now we can show that the sum of the first and third terms of
Eq. (112) is positive definite:
 |
(125) |
The last step is due to the Cauchy-Schwarz inequality. Also, as
 , the second term of Eq. (98)
is positive definite
, the second term of Eq. (98)
is positive definite
 |
(126) |
Combining these two results, we get
 |
(127) |
i.e.,
 based on the update formular Eq. (98)
is positive definite. Following the same steps, we can also show that
based on the update formular Eq. (98)
is positive definite. Following the same steps, we can also show that
 based on Eq. (117) is positive definite.
based on Eq. (117) is positive definite.
Examples:
The figures below shows the search path of the DFP and BPGS methods
when applied to find the minimum of the Rosenbrock function.
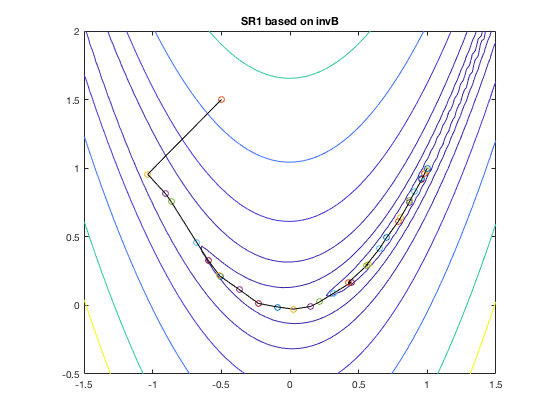
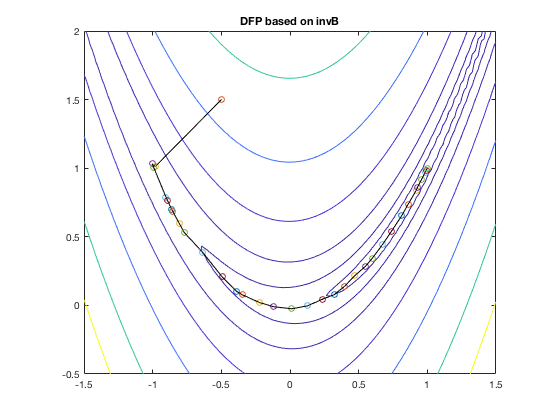
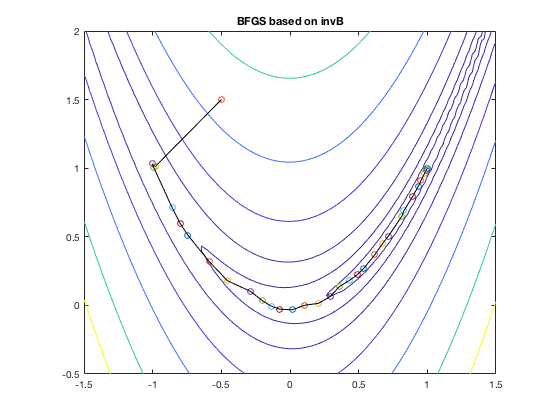
 :
:

 is the Jacobian matrix of
is the Jacobian matrix of
 ,
,
 :
:

 and
and
 are the gradient vector and
Hessian matrix of
are the gradient vector and
Hessian matrix of
 at
at  , respectively.
, respectively.









 , we get
, we get

 , we have
, we have
 ,
and the above can be written as
,
and the above can be written as





 is the secant approximation of the Hessian
matrix
is the secant approximation of the Hessian
matrix  , and the last eqality is called the
secant equation. For convenience, we further define:
, and the last eqality is called the
secant equation. For convenience, we further define:

 or
or
 , or its inverse
, or its inverse
 , in any of the
quasi-Newton algorithms, all taking the follow general steps:
, in any of the
quasi-Newton algorithms, all taking the follow general steps:
 and
and  , set
, set  ;
;
 and the search direction
and the search direction
 ;
;
 with step
size
with step
size  satisfying the
Wolfe conditions.
satisfying the
Wolfe conditions.
 or
or
 ,
that satisfies the quasi-Newton equation;
,
that satisfies the quasi-Newton equation;
 , go back
to second step.
, go back
to second step.
 ,
,
 must be positive definite matrix, same as the Hessian
matrix
must be positive definite matrix, same as the Hessian
matrix  it approximates. Specially, if
it approximates. Specially, if
 ,
then
,
then
 , the algorithm becomes the gradient
descent method; also, if
, the algorithm becomes the gradient
descent method; also, if
 is the Hessian matrix,
then the algorithm becomes the Newton's method.
is the Hessian matrix,
then the algorithm becomes the Newton's method.







 a vector and
a vector and
 is a matrix of rank 1.
Imposing the secant condition, we get
is a matrix of rank 1.
Imposing the secant condition, we get
 i.e.,
i.e.,
 is in the same direction as
is in the same direction as
 , and can therefore
be written as
, and can therefore
be written as
 . Substituting this back we get
. Substituting this back we get

 ,
,

 becomes
becomes

 :
:





 and
and
 . Specifically,
same as above, we impose the secant condition for the inverse
. Specifically,
same as above, we impose the secant condition for the inverse
 of the following form
of the following form


 .
.






 , we get
, we get



 we get
Given this update formula for
we get
Given this update formula for  , we can further find its
inverse
, we can further find its
inverse
 and then the search direction
and then the search direction
 .
.



![${\bf U}=[{\bf u}_1\;{\bf u}_2]$](img438.svg)
![${\bf V}=[{\bf v}_1\;{\bf v}_2]$](img439.svg)






![$\displaystyle {\bf B}_n^{-1}-{\bf B}_n^{-1}{\bf U}{\bf C}^{-1}{\bf V}^T{\bf B}_...
...{-1}[{\bf u}_1\;{\bf u}_2]{\bf C}^{-1}
({\bf B}_n^{-1}[{\bf v}_1\;{\bf v}_2])^T$](img443.svg)
![$\displaystyle {\bf C}=\left[\begin{array}{cc}c_{11} & c_{12}\\ c_{21} & c_{22}\...
...1}{\bf U}
={\bf I}+[{\bf v}_1\;{\bf v}_2]^T{\bf B}^{-1}_n[{\bf u}_1\;{\bf u}_2]$](img444.svg)




![$\displaystyle {\bf C}=\left[\begin{array}{cc}c_{11} & c_{12}\\ -c_{12} & 0\end{...
...t[\begin{array}{cc}0 & -1/c_{12}\\ 1/c_{12} & c_{11}/c_{12}^2\end{array}\right]$](img449.svg)
 into the expression for
into the expression for
 , we get:
, we get:







 :
In summary,
:
In summary,
 can be found by either Eq.
(98) for
can be found by either Eq.
(98) for
 followed by an additional
inversion operation, or Eq. (112) directly for
followed by an additional
inversion operation, or Eq. (112) directly for
 . The results obtained by these methods are
equivalent.
. The results obtained by these methods are
equivalent.



 and
and  are real scalars,
are real scalars,  and
and  are vectors. Imposing the secant condition for the inverse of
are vectors. Imposing the secant condition for the inverse of
 , we get
, we get



 we get
Following the same procedure used for the BFGS method, we can also
obtain the update formular of matrix
we get
Following the same procedure used for the BFGS method, we can also
obtain the update formular of matrix  for the DFP method:
for the DFP method:




 i.e.
i.e.
 by
by
 , we get:
, we get:



 and
and  . We therefore have
. We therefore have

 , we can further prove by
induction that both
, we can further prove by
induction that both
 and
and
 based repectively on the update formulae in Eqs.
(98) and (117) are positive
definite. We first assume
based repectively on the update formulae in Eqs.
(98) and (117) are positive
definite. We first assume  and
and  are both
positive definite, and express
are both
positive definite, and express  in terms of its
Cholesky decomposition,
in terms of its
Cholesky decomposition,
 . We further
define
. We further
define
 ,
,
 ,
and get
,
and get


 , the second term of Eq. (98)
is positive definite
, the second term of Eq. (98)
is positive definite


 based on the update formular Eq. (98)
is positive definite. Following the same steps, we can also show that
based on the update formular Eq. (98)
is positive definite. Following the same steps, we can also show that
 based on Eq. (117) is positive definite.
based on Eq. (117) is positive definite.


