Next: Issues of Local/Global Minimum Up: Unconstrained Optimization Previous: Quasi-Newton Methods
The gradient descent method can be used to solve the minimization problem
when the Hessian matrix of the objective function is not available. However,
this method may be inefficient if it gets into a zigzag search pattern and
repeat the same search directions many times. This problem can be avoided
in the conjugate gradient (CG) method.
If the objective function is quadratic, the CG method converges to the
solution in 
Again consider the approximation of the function

 |
(128) |
 has a
minimum. If function
has a
minimum. If function
 is quadratic, the approximation
above becomes exact and the function can be written as
is quadratic, the approximation
above becomes exact and the function can be written as
 |
(129) |
 is the symmetric Hessian matrix, and its
gradient and Hessian can be written as the following respectively:
is the symmetric Hessian matrix, and its
gradient and Hessian can be written as the following respectively:
 |
(130) |
 |
(131) |
 , we get the
solution
, we get the
solution
 , at which the function is minimized
to
, at which the function is minimized
to
 |
(132) |
 that minimizes
that minimizes
 , its gradient is
, its gradient is
We also see that the minimization of the quadratic function



Conjugate basis vectors
We first review the concept of
conjugate vectors, which is
of essential importance in the CG method. Two vectors 


 |
(134) |
 , the two conjugate vectors become orthogonal
to each other, i.e.,
, the two conjugate vectors become orthogonal
to each other, i.e.,
 .
.
Similar to a set of 




Also we note that any set of 

Example:
Given two independent basis vectors of the 2-D space, and a positive-definite matrix:
![$\displaystyle {\bf v}_1=\left[\begin{array}{r}1\\ 0\end{array}\right],\;\;\;\;\...
...y}\right],\;\;\;\;\;
{\bf A}=\left[\begin{array}{rr}3&1\\ 1&2\end{array}\right]$](img507.svg) |
![$\displaystyle {\bf u}_1={\bf v}_1=\left[\begin{array}{r}1\\ 0\end{array}\right]...
...1^T{\bf A}{\bf u}_1}{\bf u}_1
=\left[\begin{array}{c}-1/3\\ 1\end{array}\right]$](img508.svg) |
![${\bf x}=[2,\;3]^T$](img509.svg) onto
onto  and
and  are:
are:
![$\displaystyle {\bf p}_{{\bf v}_1}({\bf x})=\frac{{\bf v}_1^T{\bf x}}{{\bf v}_1^...
...array}{c}0\\ 1\end{array}\right]
=\left[\begin{array}{c}0\\ 3\end{array}\right]$](img512.svg) |
 onto
onto  and
and  are:
are:
![$\displaystyle {\bf p}_{{\bf u}_1}({\bf x})=\frac{{\bf u}_1^T{\bf A}{\bf x}}
{{\...
...y}{c}-1/3\\ 1\end{array}\right]
=\left[\begin{array}{c}-1\\ 3\end{array}\right]$](img515.svg) |
 can be represented in either of the two bases:
can be represented in either of the two bases:
![$\displaystyle {\bf x}=\left[\begin{array}{c}2\\ 3\end{array}\right]$](img516.svg) |
 |
![$\displaystyle 2\left[\begin{array}{c}1\\ 0\end{array}\right]
+3\left[\begin{arr...
...{\bf v}_1+3{\bf v}_2
={\bf p}_{{\bf v}_1}({\bf x})+{\bf p}_{{\bf v}_2}({\bf x})$](img517.svg) |
|
 |
![$\displaystyle 3\left[\begin{array}{c}1\\ 0\end{array}\right]
+3\left[\begin{arr...
...{\bf u}_1+3{\bf u}_2
={\bf p}_{{\bf u}_1}({\bf x})+{\bf p}_{{\bf u}_2}({\bf x})$](img518.svg) |
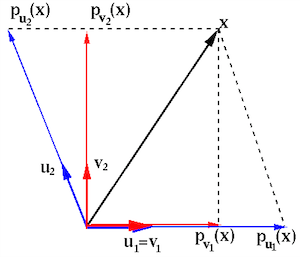
Search along a conjugate basis
Similar to the gradient descent method, which iteratively improves
the estimated solution by following a sequence of orthogonal
search directions





 .
Then subtracting
.
Then subtracting  from both sides, we get the iteration
in terms of the errors:
Due to
from both sides, we get the iteration
in terms of the errors:
Due to
 in Eq. (133), we can find the
gradient at the nth step
in Eq. (133), we can find the
gradient at the nth step  as
As the gradient at the solution is zero
as
As the gradient at the solution is zero
 ,
we can consider the gradient
,
we can consider the gradient  at
at  as the
residual of the nth iteration, and
as the
residual of the nth iteration, and
 an error measurement representing how close
an error measurement representing how close  is to the
true solution
is to the
true solution  .
.
The optimal step size given in Eq. (60) can now be
written as
 and
and  are A-orthogonal,
are A-orthogonal,
 .
Substituting this into Eq. (136) we get
.
Substituting this into Eq. (136) we get
 |
(139) |
 associated with the initial guess
associated with the initial guess  as a linear combination
of the A-orthogonal search vectors
as a linear combination
of the A-orthogonal search vectors
 as
as  basis vectors that span the N-D vector space:
where
basis vectors that span the N-D vector space:
where
 is the A-projection of
is the A-projection of  onto the ith basis vector
onto the ith basis vector  :
:
 |
(141) |
 happens to be the negative optimal step
size in Eq. (138):
happens to be the negative optimal step
size in Eq. (138):
 |
(142) |
 in Eq. (136) can be written as
in Eq. (136) can be written as
 |
(143) |
 is reduced by one, i.e., the nth component
is reduced by one, i.e., the nth component
 of
of  along the direction
of
along the direction
of  is completely eliminated. After
is completely eliminated. After  such iterations,
the error is reduced from
such iterations,
the error is reduced from  to
to
 , and the
true solution is obtained
, and the
true solution is obtained
 .
.
Pre-multiplying

 |
(144) |
 iterations the remaining error
iterations the remaining error
 is A-orthogonal to all previous directions
is A-orthogonal to all previous directions
 .
.
Due to Eq. (137), the equation above can also be written as
i.e., the gradient is orthogonal to all previous
search directions.
is orthogonal to all previous
search directions.
In the figure below, the conjugate gradient method is compared with
the gradient descent method for the case of 







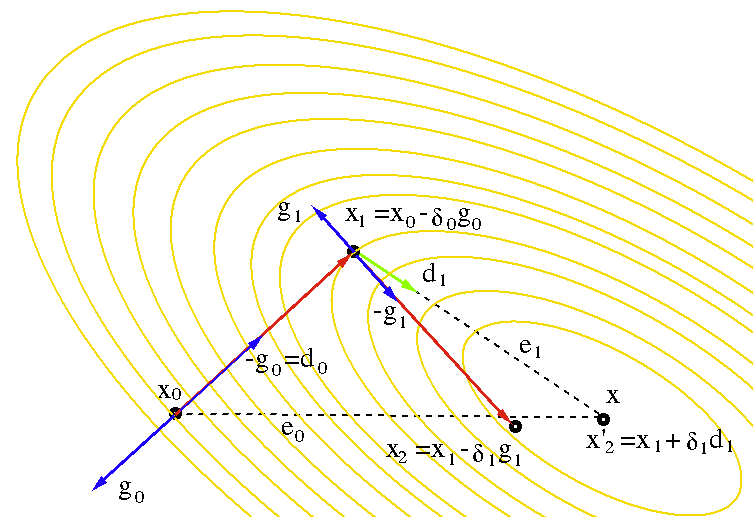 .
.
Find the A-orthogonal basis
The 



 and
and
 is the A-projection of
is the A-projection of  onto each
of the previous direction
onto each
of the previous direction  .
.
We will gain some significant computational advantage if we choose
to use

 can be written
as a linear combination of all previous search directions
can be written
as a linear combination of all previous search directions
 :
:
 |
(149) |
 on both sides, we get
on both sides, we get
 |
(150) |
 in Eq. (145).
We see that
in Eq. (145).
We see that
 is also orthogonal to all previous gradients
is also orthogonal to all previous gradients
 .
.
Pre-multiplying

 |
(151) |
 for all
for all  (Eq. (145)). Substituting
(Eq. (145)). Substituting
 into Eq. (138), we get
Next we consider
into Eq. (138), we get
Next we consider
 |
(153) |
 with
with  on both sides we get
on both sides we get
 |
(154) |
 (
( ). Solving for
). Solving for
 we get
we get
 |
(155) |
 |
(156) |
which is non-zero only when 




 (Eq. (152)) into the above expression for
(Eq. (152)) into the above expression for
 ,
we get
We note that matrix
,
we get
We note that matrix  no longer appears in the expression.
no longer appears in the expression.
The CG algorithm
Summarizing the above, we finally get the conjugate gradient algorithm in the following steps:
 and initialize the search direction (same as gradient
descent):
and initialize the search direction (same as gradient
descent):
 |
(159) |
 is smaller
than a preset threshold. Otherwise, continue with the following:
is smaller
than a preset threshold. Otherwise, continue with the following:
 |
(160) |
 |
(161) |
 |
(162) |
 |
(163) |
 and go back to step 2.
and go back to step 2.
The algorithm above assumes the objective function








The Matlab code for the conjugate gradient algorithm is listed below:
function xn=myCG(o,tol) % o is the objective function to minimize
syms d; % variable for 1-D symbolic function f(d)
x=symvar(o).'; % symbolic variables in objective function
O=matlabFunction(o); % the objective function
G=jacobian(o).'; % symbolic gradient of o(x)
G=matlabFunction(G); % the gradient function
xn=zeros(length(x),1); % initial guess of x
xc=num2cell(xn);
e=O(xc{:}); % initial error
gn=G(xc{:}); % gradient at xn
dn=-gn; % use negative gradient as search direction
n=0;
while e>tol
n=n+1;
f=subs(o,x,xn+d*dn); % convert n-D f(x) to 1-D f(d)
delta=Opt1d(f); % find delta that minimizes 1D function f(d)
xn=xn+delta*dn; % updata variable x
xc=num2cell(xn);
e=O(xc{:}); % new error
gn1=G(xc{:}); % new gradient
bt=-(gn1.'*gn1)/(gn.'*gn); % find beta
dn=-gn1-bt*dn; % new search direction
gn=gn1; % update gradient
fprintf('%d\t(%.4f, %.4f, %.4f)\t%e\n',n,xn(1),xn(2),xn(3),e)
end
end
Here is the function that uses Newton's method to find the optimal
step size  that minimizes the objective function as a 1-D
function of
that minimizes the objective function as a 1-D
function of  :
:
function x=Opt1d(f) % f is 1-D symbolic function to minimize
syms x;
tol=10^(-3);
d1=diff(f); % 1st order derivative
d2=diff(d1); % 2nd order derivative
f=matlabFunction(f);
d1=matlabFunction(d1);
d2=matlabFunction(d2);
x=0.0; % initial guess of delta
if d2(x)<=0 % second order derivative needs to be greater than 0
x=rand-0.5;
end
y=x+1;
while abs(x-y) > tol % minimization
y=x;
x=y-d1(y)/d2(y); % Newton iteration
end
end
Example:
To compare the conjugate method and the gradient descent method, consider a very simple 2-D quadratic function
![$\displaystyle f(x,y)={\bf x}^T{\bf A}{\bf x}
=[x_1,\,x_2]\left[\begin{array}{cc}3&1\\ 1&2\end{array}\right]
\left[\begin{array}{c}x_1\\ x_2\end{array}\right]$](img600.svg) |
![${\bf x}_0=[1.5,\;-0.75]^T$](img601.svg) ,
the iteration gets into a zigzag pattern and the convergence is very slow,
as shown below:
,
the iteration gets into a zigzag pattern and the convergence is very slow,
as shown below:
![\begin{displaymath}\begin{array}{c\vert c\vert c}\hline
n & {\bf x}=[x_1,\,x_2] ...
...
13 & 0.000005, -0.000016 & 2.153408e-10 \\ \hline
\end{array}\end{displaymath}](img602.svg) |
 steps from any initial guess to reach at the solution:
steps from any initial guess to reach at the solution:
![\begin{displaymath}\begin{array}{c\vert c\vert c}\hline
n & {\bf x}=[x_1,\,x_2] ...
...\
2 & 0.000000, -0.000000 & 1.155558e-33 \\ \hline
\end{array}\end{displaymath}](img603.svg) |
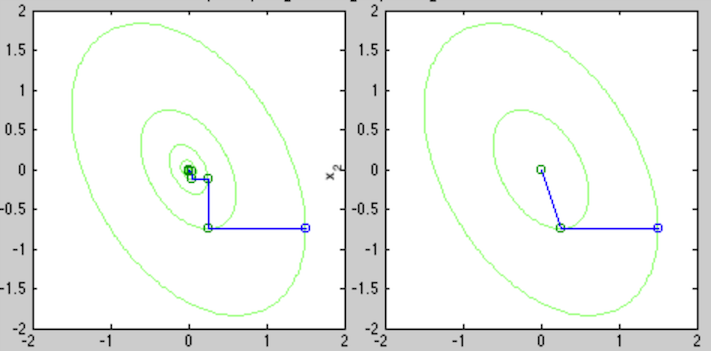
For an 

![$\displaystyle {\bf A}=\left[\begin{array}{ccc}5 & 3 & 1\\ 3 & 4 & 2\\ 1 & 2 & 3
\end{array}\right]$](img605.svg) |
![${\bf x}_0=[1,\;2,\;3]^T$](img606.svg) , it takes the gradient
descent method 41 iterations to reach
, it takes the gradient
descent method 41 iterations to reach
![${\bf x}_{41}=[3.5486e-06,\;-7.4471e-06,\;4.6180e-06]^T$](img607.svg) corresponding
to
corresponding
to
 . From the same initial guess, it takes the
conjugate gradient method only
. From the same initial guess, it takes the
conjugate gradient method only  iterations to converge to the
solution:
iterations to converge to the
solution:
 |
For an 


Example:
The figure below shows the search path of the conjugate gradient method applied to the minimization of the Rosenbrock function:
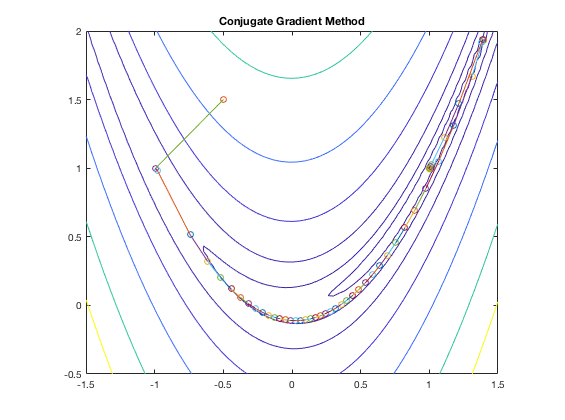
Example:
Solve the following 
 |
 .
.
This equation system can be represented in vector form as



 |
In comparison, the gradient descent method would need to take over 200 iterations (with much reduced complexity though) to reach this level of error.
Conjugate gradient method used for solving linear equation systems:
As discussed before, if 




Now consider solving the linear system









 |
(164) |
![$\displaystyle {\bf b}={\bf A}{\bf x}={\bf A}\left[\sum_{i=1}^N c_i{\bf d}_i\right]
=\sum_{i=1}^N c_i{\bf A}{\bf d}_i$](img621.svg) |
(165) |
 on both sides we get
on both sides we get
 |
(166) |
 we get
we get
 |
(167) |
 we get the solution
of the equation:
we get the solution
of the equation:
 |
(168) |
 , the ith term of the summation above
is simply the A-projection of
, the ith term of the summation above
is simply the A-projection of  onto the ith direction
onto the ith direction  :
:
 |
(169) |
One application of the conjugate gradient method is to solve the normal
equation to find the least-square solution of an over-constrained equation
system





 |
(170) |
 is an
is an  by
by  symmetric, positive definite matrix.
This normal equation can be solved by the conjugate gradient method.
symmetric, positive definite matrix.
This normal equation can be solved by the conjugate gradient method.