AC equivalent circuits

The transistor amplifier in the example here has a voltage gain of 150, based on the assumption of zero internal resistance $R_S=0$ in its source and infinite load resistance $R_L=\infty$. But, as discussed before, the voltage a circuit receives from a source depends on its input impedance $r_{in}$ as well as the internal impedance $R_s\ne 0$ of the source, while the voltage it delivers depends on its output impedance $r_{out}$ as well as the load impedance $R_L$. It is therefore important to consider these input and output impedances of an amplification circuit as well as its voltage gain.

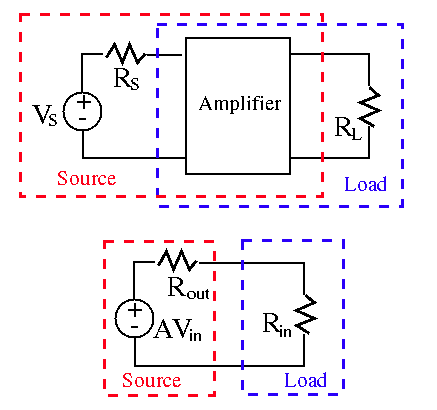
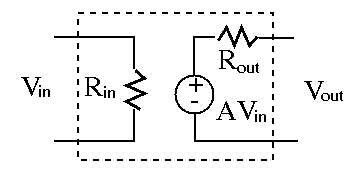
In the first figure, everything inside the red box, including the amplifier as well as $V_S$ and $R_s$, is treated as the source, while everything inside the blue box, including the amplifier as well as $R_L$, is treated as the load. Given the amplifier as well as the source $V_S$ and $R_s$, and the load $R_L$, we need to find the following three parameters so that the red and blue boxes in the first figure can be modeled by the corresponding boxes in the second figure:

• Input impedance $r_{in}$
• Output impedance $r_{out}$
• voltage gain $A$

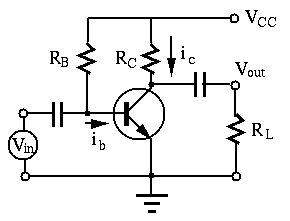
Consider the typical transistor AC amplification circuit below:

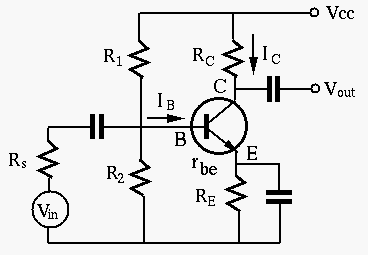
If the capacitances of the coupling capacitors and the emitter by-pass capacitor are large enough with respect to the frequency of the AC signal in the circuit is high enough, these capacitors can all be approximated as short circuit. Moreover, note that the AC voltage of the voltage supply $V_{CC}$ is zero, it can be treated the same as the ground. Now the AC behavior of the transistor amplification circuit can be modeled by the following small signal equivalent circuit:

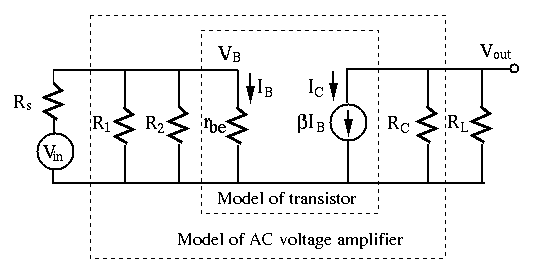
As shown above, this AC small signal equivalent circuit can be modeled by as an active circuit containing three components:

• AC Input Impedance:

  For AC signals, the input of the amplification circuit is shown below, where $R_s$ is the internal resistance of the signal source, and the input impedance of the circuit is the three resistances $R_1$, $R_2$ and $r_{be}$ in parallel:

  $$r_{in}=R_1\vert\vert R_2\vert\vert r_{be} =\left(\frac{1}{R_1}+\f... ...}}\right)^{-1} =\frac{R_1 R_2 r_{be}}{R_1R_2+R_1r_{be}+R_2r_{be}}\approx r_{be}$$ (68)

  The approximation is due to the fact that typically $R_1,\;R_2\gg r_{be}$.
• AC Output Impedance:

  This is simply the resistance of the resistor $r_{out}=R_C$.

• AC Voltage Gain:

  Given the AC input voltage $v_{in}$, the base voltage and current are

  $$v_b \approx v_{in}\;\frac{r_{be}}{r_{be}+R_s},\;\;\;\;\;\;\;\;\;\; i_b=\frac{v_b}{r_{be}}\approx \frac{v_{in}}{r_{be}+R_s}$$ (69)

  The collector current is $i_c=\beta i_b$ and collect voltage is

  $$v_{out}=v_c\approx -i_c\;(R_C\vert\vert R_L) = -\beta\;i_b\;(R_C\vert\vert R_L) =-\beta \frac{v_{in}}{r_{be}+R_s} (R_C\vert\vert R_L)$$ (70)

  Here the negative sign indicates the fact that $v_c$ is $180^\circ$ out of phase with $v_b$. The voltage gain is:

  $$A=\frac{v_{out}}{v_{in}}=\frac{v_c}{v_{in}} \approx -\beta \frac{R_C\vert\vert R_L}{r_{be}+R_s}$$ (71)

  If

  $$R_s\ll r_{in}=R_1\vert\vert R_2\vert\vert r_{be} \approx r_{be},\;\;\;\;\;R_L\gg r_{out}=R_C$$ (72)

  then the gain can be approximated as

  $$A=\frac{v_{out}}{v_{in}}\approx -\beta \frac{R_C}{r_{be}}$$ (73)

  To achieve higher gain $A$, we want to have smaller $r_{be}$ and greater $R_C$. However, this also means the input resistance $r_{in}\approx r_{be}$ is small and the output resistance $r_{out}\approx R_C$ is large, neither is desirable.

  Note that $r_{be}$ is not constant. As shown before, $r_{be}\approx \eta\;V_T/I_B$ of the base-emitter PN-junction is approximately inversely proportional to $I_B$.

  Also note that $R_C$ and $I_B$ affects the DC operating point. Distortion may be caused if $R_C$ or $I_B$ is set properly.

Example 1:

$V_{CC}=12V$, $R_B=300\,k\Omega$, $R_C=R_L=4\,k\Omega$, and $\beta=40$. We further assume $R_s=0$, and the capacitances are large enough so that they can be considered as short circuit for AC signals.

• Find base current:

  $$I_B=\frac{V_{CC}-V_{BE}}{R_B} \approx \frac{V_{CC}}{R_B}=\frac{12}{300\times 10^3} =40\times 10^{-6}\; A=40\;\mu A$$ (74)

• Find DC load line determined by the following two points:
  

  $$I_C=0, V_{CE}=12V$$

  $$V_{CE}=0, I_C=\frac{V_{CC}}{R_C}=\frac{12\;V}{4\times 10^3\;\Omega} =3\times 10^{-3}A=3 \;mA$$ (75)

  
  

• Find DC operating point $Q$:

  $$I_C=\beta I_B=40\times 40\;\mu A=1.6\;mA,\;\;\;\;\;\;\; V_{CE}=V_{CC}-R_CI_C=12-4\times 1.6=5.6\;V$$ (76)

• Find AC load line:

  The AC load is $R'_L=R_C\vert\vert R_L=2\;k\Omega$. The AC load line is a straight line passing the DC operating point with slope $1/R'_L=1/2$. The intersections of the AC load line with $V_{CE}$ and $I_C$ axes can be found by

  $$\frac{1.6}{V_{AC0}-5.6}=\frac{1}{2}\;\;\;\;\Longrightarrow V_{AC0}=8.8\,V$$ (77)

  $$\frac{I_{AC0}-1.5}{5.6}=\frac{1}{2}\;\;\;\;\Longrightarrow I_{AC0}=4.4\;mA$$ (78)

• Find input AC voltage and current:

  Assume AC input voltage is $v_{in}=(20\;\sin\;\omega t)\;mV$ and $V_{BE}=0.6V$, the overall base voltage is

  $$v_{be}(t)=V_{BE}+v_{in}=(0.6+0.02\;\sin\;\omega t)\;V$$ (79)

  and the corresponding base current can be found graphically from the input characteristics to be

  $$i_b(t)=I_B+i_{in}=(40+20\;\sin\;\omega t)\;\mu A$$ (80)

  between 20 and 60 $\mu A$.

• Find $r_{be}$

  As shown here,

  $$r_{be}=\eta \frac{V_T}{I_B}=1.5\times\frac{26\;mV}{40\mu A} \approx 1 \;k\Omega$$ (81)

  which can also be estimated from the input characteristic plot below:

  $$r_{be}=\frac{\Delta v_{be}}{\Delta i_b} =\frac{20\,mV}{20\,\mu A}=1\;k\Omega$$ (82)

• Find AC output voltage:

  The output current is

  $$i_c(t)=\beta\; i_b(t)=40\times(40+20\sin\omega t)\;\mu A =(1.6+ 0.8 \;\sin\omega t)\,mA$$ (83)

  The output voltage is

  $$v_c(t)=V_{AC0}-R'_L\;i_c(t)=8.8-2\times(1.6+0.8\;\sin\omega t) =(5.6-1.6 \;sin\;\omega t)\;V=v_{out}(t)$$ (84)

• Find the AC voltage gain:

  $$A_v=\frac{\vert v_{out}\vert}{\vert v_{in}\vert}=\frac{1.6}{0.02}=80$$ (85)

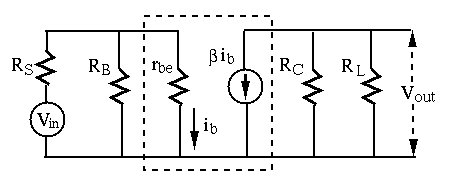
The circuit above can also be analyzed using the small-signal model.

$$i_b=v_{in}/r_{be}, \;\;\;\;v_c=-i_c\; (R_C\vert\vert R_L)$$ (86)

The voltage gain is:

$$A_v=\frac{v_c}{v_{in}}=-\frac{\beta\; i_b\;(R_C\vert\vert R_L)}{r... ...ta\,(R_C\vert\vert R_L)}{r_{be}} =-\frac{(40\times 2)\;k\Omega}{1\;k\Omega}=-80$$ (87)

The input resistance is $r_{in}=R_B\vert\vert r_{be}\approx r_{be}=1\,k\Omega$, the output resistance is $r_{out}=R_C=4\;k\Omega$.

Example 2:

Consider the circuit below with its AC small-signal model:

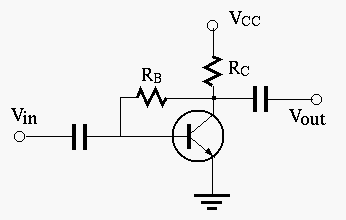
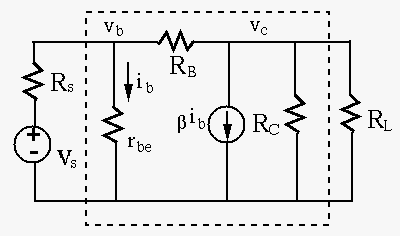
We can find the voltage gain, the input and output resistances when $R_S=0$ and $R_L=\infty$ ( $v_{in}=v_b,\;\;v_{out}=v_c$).

• AC voltage gain:

  Apply KCL to the collector to get

  $$\frac{v_c-v_s}{R_B}+\beta i_b+\frac{v_c}{R_C} =\frac{v_c-v_s}{R_B}+\beta \,\frac{v_s}{r_{be}}+\frac{v_c}{R_C}=0$$ (88)

  i.e.,

  $$v_c\left(\frac{1}{R_B}+\frac{1}{R_C}\right) =v_s\left(\frac{1}{R_B}-\beta\frac{1}{r_{be}}\right)$$ (89)

  Solving this we get $v_c$ and then find the AC voltage gain:
  

  $$A = \frac{v_{out}}{v_{in}}=\frac{v_c}{v_s} =\frac{1/R_B-\beta/r_{be}}{1/R_B+1/R_C} =\frac{R_C(r_{be}-\beta R_B)}{(R_B+R_C)r_{be}}$$

  $$\approx-\beta \,\frac{R_C R_B}{(R_B+R_C)r_{be}} = -\beta \frac{R_B\vert\vert R_C}{r_{be}} \stackrel{R_B\rightarrow\infty}{\Longrightarrow}-\beta\frac{R_C}{r_{be}}$$ (90)

  
  where the approximation is due to the fact that $r_{be}\ll \beta R_B$. We see that when $R_B\rightarrow\infty$, i.e., there is not negative feedback, the gain becomes the same as the result before without feedback.

• AC input resistance:

  The input resistance is the parallel combination of $r_{be}$ and $r'_{in}$, the resistence of the circuit to the right of the base. First, we realize that $i_b=v_b/r_{be}=v_s/r_{be}$, and convert the current source $\beta i_b$ in parallel with $R_C$ to a voltage source $\beta i_bR_C$ in series with $R_C$, and then get the current into the circuit as:

  $$i=\frac{v_b-(-R_C\beta i_b)}{R_B+R_C}=\frac{v_b+R_C \beta v_b/r_{... ...rac{1+R_C \beta /r_{be}}{R_B+R_C} \approx v_b \frac{\beta R_C /r_{be}}{R_B+R_C}$$ (91)

  where the approximation is due to the fact that $r_{be}\ll \beta R_C$. The resistance can then be found as

  $$r'_{in}=\frac{v_b}{i} =\frac{R_B+R_C}{\beta R_C /r_{be}}=\frac{R_B+R_C}{\beta R_C}\,r_{be}$$ (92)

  and the total input resistance is:

  $$r_{in}=r_{be}\vert\vert r'_{in}=r_{be}\frac{1}{1+\beta R_C/(R_B+R... ...be} & R_B\rightarrow\infty\\ r_{be}/\beta & R_B\rightarrow 0\end{array}\right.$$ (93)

• AC output resistance:
  • Open-circuit voltage with $R_L=\infty$ is simply

    $$v_{oc}=A v_b=-\beta\frac{R_C}{r_{be}}\frac{1}{1+R_C/R_B}\,v_b$$ (94)

  • Short-circuit current with $R_L=0$:

    The short-circuit current by $v_b$ alone is $i'=v_b/R_B$, and the short-circuit current by current source $\beta i_b$ alone is $i''=-\beta i_b=-\beta v_b/r_{be}$, then by superposition, the total short-circuit current is

    $$i_{sc}=i'+i''=v_b\left(\frac{1}{R_B}-\frac{\beta}{r_{be}}\right)$$ (95)

  • Output resistance:
    

    $$r_{out} = \frac{v_{oc}}{i_{sc}}=\frac{-\beta\frac{R_C}{r_{be}}\frac{1}{1+R_... ...beta\frac{R_C}{r_{be}}\frac{1}{1+R_C/R_B}}{\frac{r_{be}-\beta R_B}{R_B r_{be}}}$$

    $$\approx \frac{-\beta\frac{R_C}{r_{be}}\frac{R_B}{R_B+R_C}}{\frac{-\beta R... ...}{R_C+R_B}=R_C\vert\vert R_B\stackrel{R_B\rightarrow\infty}{\Longrightarrow}R_C$$ (96)

    
    

Example 3:

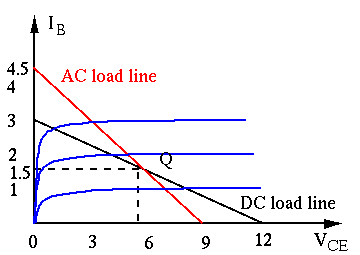
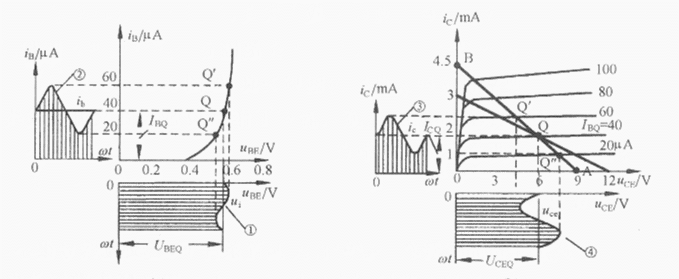
Consider both the DC operating point and its AC small signal model of the circuit below, where $V_{CC}=12V,\;R_E=0.1\,k\Omega,\;\beta=100$:

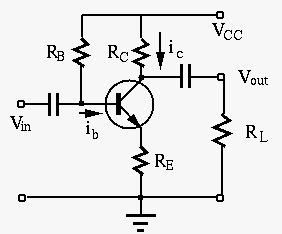
We realize $R_E$ introduces a negative feedback:

$$i_c \uparrow \Longrightarrow v_e \uparrow \Longrightarrow v_{be} \downarrow \Longrightarrow i_b \downarrow \Longrightarrow i_c \downarrow$$ (97)

We first apply KVL to the base path to get

$$V_{CC}=I_B R_B+V_{BE}+(\beta+1)I_BR_E,\;\;\;\;\; I_B=\frac{V_{CC}-V_{BE}}{R_B+(\beta+1)R_E}$$ (98)

and

$$I_C=\beta I_B=\beta\,\frac{V_{CC}-V_{BE}}{R_B+(\beta+1)R_E},\;\;\;\;\; V_{CE}=V_{CC}-I_CR_C-I_ER_E\approx V_{CC}-I_C(R_C+R_E)$$ (99)

We then find $R_B$ and $R_C$ so that the DC operating point to be in the middle of the linear region:

• We can find $R_B$ assuming $R_C=1.9\,k\Omega$:

  $$I_E=\frac{V_{CC}-V_{CE}}{R_C+R_E}=\frac{6}{0.1+1.9}=3\,mA,\;\;\;\; I_B=\frac{I_C}{\beta}=0.03\,mA$$ (100)

  $$R_B+(\beta+1)R_E=\frac{V_{CC}-V_{BE}}{I_B}=\frac{12-0.7}{0.03}=377\,k\Omega$$ (101)

  $$R_B=377-100\times 0.1=367\,k\Omega$$ (102)

• Alternatively, we find $R_C$ assuming $R_B=250\,k\Omega$:

  $$I_B=\frac{V_{CC}-V_{BE}}{R_B+\beta R_E} =\frac{12-0.7}{250+100\times 0.1}=\frac{11.3}{260}=0.044$$ (103)

  $$\frac{V_{CC}-V_{CE}}{R_C+R_E}=\frac{6}{0.1+R_C}=I_C=\beta I_B=4.4\,mA$$ (104)

  Solving to get $R_C=1.26\,k\Omega$.

Next consider the AC equivalent circuit based on small-signal model of the transistor in the dashed line box:

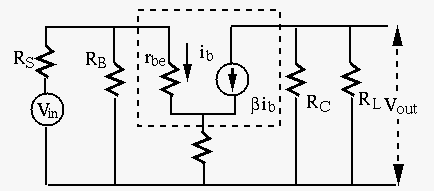
As $R_B$ is significantly greater than all resistors in the circuit, it can be ignored in the AC analysis. Apply KCL to the emitter to get

$$i_b+\beta i_b=(\beta+1)i_b=\frac{v_e}{R_E}=\frac{v_{in}-r_{be}i_b}{R_E}$$ (105)

Solving for $i_b$:

$$i_b=\frac{v_{in}}{r_{be}+(\beta+1)R_E}$$ (106)

• AC input resistance:

  $$r_{in}=\frac{v_{in}}{i_{in}}=\frac{v_{in}}{i_b}=r_{be}+(\beta+1)R_E \approx \beta R_E$$ (107)

• AC voltage gain:
  

  $$A = \frac{v_{out}}{v_{in}}=-\frac{\beta i_b (R_C\vert\vert R_L)}{v_{i... ...=-\frac{\beta\,(R_C\vert\vert R_L)}{v_{in}}\,\frac{v_{in}}{r_{be}+(\beta+1)R_E}$$

  $$= -\frac{\beta\,R_C\vert\vert R_L}{r_{be}+(\beta+1)R_E} \approx -\frac{R_C\vert\vert R_L}{R_E}$$ (108)

  
  
• AC output resistance:
  • Open-circuit voltage ( $R_L=\infty$): $v_{oc}=-i_c R_C=-\beta i_b R_C$
  • Short-ciruit current ($R_L=0$): $i_{sc}=-i_c=-\beta i_b$
  • Output resistance:

    $$r_{out}=\frac{v_{oc}}{i_{sc}}=R_C$$ (109)

In conclusion, the negative feedback introduced by $R_E$ increases the input resistance, and stabalizes the DC operating point as well as the AC voltage gain.