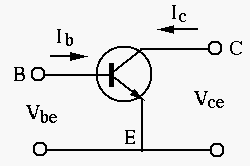
Next: AC equivalent circuits Up: ch4 Previous: Biasing
A CE transistor circuit can be modeled by a two-port network as shown below:
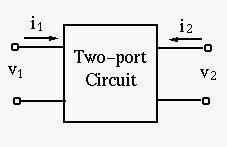
The two-port network is described by the relationship between
two pairs of variables (

![$C_4^2=4!/[2!(4-2)!]=6$](img331.svg)
 |
(63) |
 ,
,  ,
,
 , and
, and
 :
:
 |
(64) |
 |
(65) |
 are the hybrid model parameters:
are the hybrid model parameters:
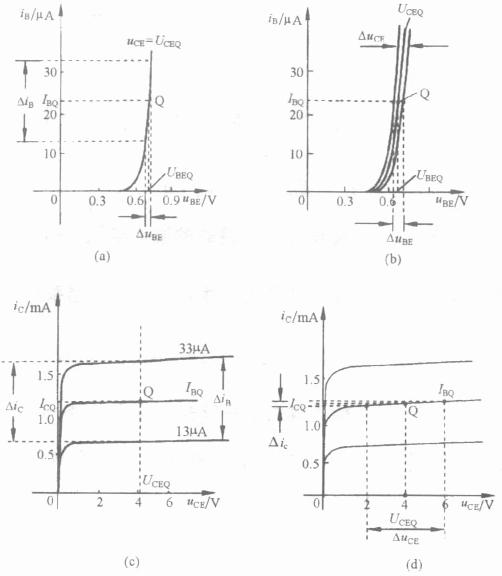
 : input AC impedance
with
: input AC impedance
with  (output AC short-circuit). This is the AC
resistance between base and emitter, the reciprocal of the
slope of the current-voltage curve of the input characteristics.
(output AC short-circuit). This is the AC
resistance between base and emitter, the reciprocal of the
slope of the current-voltage curve of the input characteristics.
 : reverse transfer voltage
ratio representing how
: reverse transfer voltage
ratio representing how  affects
affects  with
with  (input
AC open-circuit). In general
(input
AC open-circuit). In general  is small and can be ignored.
is small and can be ignored.
 : forward transfer current
ratio or current amplification factor with
: forward transfer current
ratio or current amplification factor with  (output AC
short-circuit). Typically,
(output AC
short-circuit). Typically,  is in the range of 100 to
200.
is in the range of 100 to
200.
 : output admittance,
with
: output admittance,
with  (input AC open-circuit). This is the slope of the
current-voltage curve in the output characteristics. In general
(input AC open-circuit). This is the slope of the
current-voltage curve in the output characteristics. In general
 is small and can be ignored.
is small and can be ignored.
 ,
,  ,
,  and
and  are small (
are small (
 )
around the DC operating point
)
around the DC operating point  and far away from either the cutoff
or the saturation region, the non-linear quantities that describe the
input and output characteristics can be linearized as the following
small signal model:
and far away from either the cutoff
or the saturation region, the non-linear quantities that describe the
input and output characteristics can be linearized as the following
small signal model:
 |
(66) |
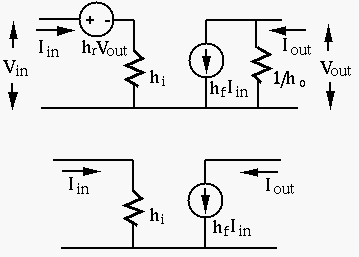
In general, 



The base and emitter forms a PN-junction with a resistance 
 |
(67) |
 through the PN-junction
between base and emitter. Typically, at room temperature
through the PN-junction
between base and emitter. Typically, at room temperature
 ,
if
,
if  is approximately in the range of
is approximately in the range of
 , then
, then
 is a few hundred ohms.
is a few hundred ohms.
Based on this small signal model, a transistor can be analyzed as a
two-port circuit containing a resistor 

In summary, we see that there are two aspects of a transistor circuit:
 ,
,  and
and  and voltages
and voltages  and
and  ;
;