Examples: Mechanical and Electrical Systems

• A mechanical system composed of a spring $k$ and a mass $m$ can be described by the following equation (Newton's second law $f=ma$):

  $$m\frac{d^2}{dt^2}x(t)+kx(t)=0,\;\;\;\; \;\;\;\; \frac{d^2}{dt^2}x(t)+\frac{k}{m}x(t)=\ddot{x}+\omega_n^2 x(t)=0$$ (61)

  where $x(t)$ is the displacement of the mass (horizontal) and $\omega_n=\sqrt{k/m}=1/\sqrt{cm}$ ($c=1/k$ is the compliance of the spring).

• An electrical system composed of a capacitor $C$ and an inductor $L$ in parallel can be described by:

  $$i_C(t)=C\frac{dv(t)}{dt},\;\;\;v(t)=L\frac{di_L(t)}{dt}$$ (62)

  where $v(t)$ is the voltage across both components, and $i_C(t)$ and $i_L(t)$ are currents through $C$ and $L$, respectively.

  

  As $i_C(t)+i_L(t)=0$, i.e. $i_C(t)=-i_L(t)$, we have

  $$v(t)=L\frac{d}{dt}i_L(t)=L\frac{d}{dt}\;(-C\frac{dv}{dt}),\;\;\; \;\;\;\;\frac{d^2v(t)}{dt^2}+\frac{1}{LC}v(t) =\ddot{v}(t)+\omega_n^2 v(t)=0$$ (63)

To find the homogeneous solution of the differential equation above (for either the mechanical or electrical system), we assume $v(t)=e^{st}$ and get $\ddot{v}(t)=s^2 e^{st}$, and the DE becomes:

$$(s^2+\omega_n^2) e^{st}=0,\;\;\;\;\;\; \;\;\;\;\;\; s^2+\omega_n^2=0$$ (64)

Solving this we get $s=\pm j\omega_n$ and

$$v(t)=e^{j\omega_n t}=\cos \omega t\pm j\sin \omega_n t$$ (65)

• In the mechanical system, when the displacement is zero $x(t) =\sin(\omega_n t)=0$, i.e., the potential energy stored in the spring is zero, the velocity $\dot{x}(t)=\omega_n\;\cos(\omega_n t)=\pm \omega_n$, i.e., the kinetic energy is maximal. On the other hand, when the displacement is $x(t)=\sin(\omega_n t)=\pm 1$, i.e., the potential energy stored in the spring is maximal, the velocity $\dot{x}(t)=\omega_n \;\cos(\omega_n t)=0$, i.e., the kinetic energy is zero.
• In the electrical system, when $v(t)=\sin(\omega_n t)=0$, i.e., the energy stored in the capacitor is zero $W_C=Cv^2/2=0$, $i(t)=C\dot{v}(t)=\omega_n C\;\cos(\omega_n t)=\pm \omega_n C$, i.e., the energy stored in the inductor $W_L=Li^2/2$ is maximal. On the other hand, when $v(t)=\sin(\omega_n t)=\pm 1$, i.e., the energy stored in the capacitor is maximal, $i(t)=C\dot{v}(t)=\omega_n C\;\cos(\omega_n t)=0$, i.e., the energy stored in the inductor is zero.

In both cases, the energy in the system is converted back and forth between different forms (potential vs. kinetic in the mechanical system, and electrical vs. magnetic in the electrical system), while the total amount is always reserved.

However, when a dash-pot (causing friction proportional to speed $\dot{x}$) is added (in parallel to the spring) in the mechanical system, and a resistor is added in series with the electrical circuit, the energy is dissipated (converted to heat) in both systems:

$$\frac{d^2x}{dt^2}+\frac{b}{m}\frac{dx}{dt}+\frac{k}{m}x=0$$ (66)

$$\frac{d^2v}{dt^2}+\frac{R}{L}\frac{dv}{dt}+\frac{1}{LC}v=0$$ (67)

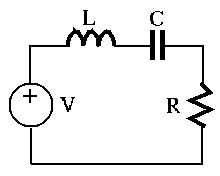
The corresponding solution of the DEs will be decaying sinusoidal, indicating the dissipation of the energy in the system.

Consider the power in the RCL electrical system:

$$p(t)=v(t) i(t) =v(t) \frac{d}{dt} Q(t)$$ (68)

The energy consumed in the system is:

$$w=\int_0^t P(\tau) d\tau=v(t) [Q(t)-Q(0)]=Cv^2(t)$$ (69)

where we have assumed $Q(0)=0$ and $Q(t)=Cv(t)$. On the other hand, as we also know the energy stored in $C$ is $W_C=Cv^2/2$, we see that half of the energy is consumed (dissipated/stored) in the rest of the circuit ($R$ and $L$). This is always the case independent of the system parameters. When the input voltage is DC $v(t)=V$, the current at the steady-state is zero and the energy stored in $L$ is $Li^2/2=0$, i.e., half of the energy from the source is dissipated by $R$. However, when $R=0$, the energy is converted back and forth between $C$ and $L$ as described above.