In general, the relationship of the currents and voltages
in an AC circuit are described by linear constant coefficient
ordinary differential equations (LCCODEs). But if only the
steady state behavior of circuit is of interested, the circuit
can be described by linear algebraic equations in the s-domain
by Laplace transform method.
Example: A low-pass filter composed of two inductors  and a capacitor
and a capacitor  is inserted between the power supply and the
appliance modeled by resistor
is inserted between the power supply and the
appliance modeled by resistor  to filter out possible spikes
(due to surges in the power line or lightning). Such spikes can
be modeled as a square impulse of certain height, e.g.,
to filter out possible spikes
(due to surges in the power line or lightning). Such spikes can
be modeled as a square impulse of certain height, e.g.,  Volt and certain duration, e.g.,
Volt and certain duration, e.g.,
 , which
can be mathematically represented by a delta function as the input
, which
can be mathematically represented by a delta function as the input
 , and we want to find out the output voltage
, and we want to find out the output voltage
 across the load resistor
across the load resistor  as the response to the impulse
input.
as the response to the impulse
input.

Time domain: We use node-voltage method applied
to the middle node  and the output node
and the output node  :
:
KCL to node  :
:
 , where
, where
 |
(294) |
 |
(295) |
KCL to node  :
:
 , where
, where
 |
(296) |
 |
(297) |
These differential equations can be combined to for a first
order differential equation system:
![$\displaystyle \frac{d}{dt}\left[\begin{array}{c}v_R\\ v_C\\ i_C\end{array}\righ...
... i_C\end{array}\right]
+\left[\begin{array}{c}0\\ 0\\ v_s/L_1\end{array}\right]$](img830.svg) |
(298) |
This first order ODE system can be written in generic form:
 |
(299) |
with a general solution:
 |
(300) |
Given the zero initial condition
 and an
input
and an
input
![${\bf x}(t)=[0,\;0,\;10^{-3}\delta(t)/L_1]^T$](img834.svg) , we can get
, we can get
![$\displaystyle v_R=[1\;0\;0]{\bf y}=e^{{\bf A}t}
\left[\begin{array}{c}0\\ 0\\ 10^{-3}/L_1\end{array}\right]$](img835.svg) |
(301) |
where
 |
(302) |
with
 and
and
![${\bf V}=[{\bf v}_1,\;{\bf v}_2,\;{\bf v}_3]$](img838.svg) being the eigenvalue
and eigenvector matrices of
being the eigenvalue
and eigenvector matrices of  satisfying
satisfying
 , i.e.,
, i.e.,
 .
.
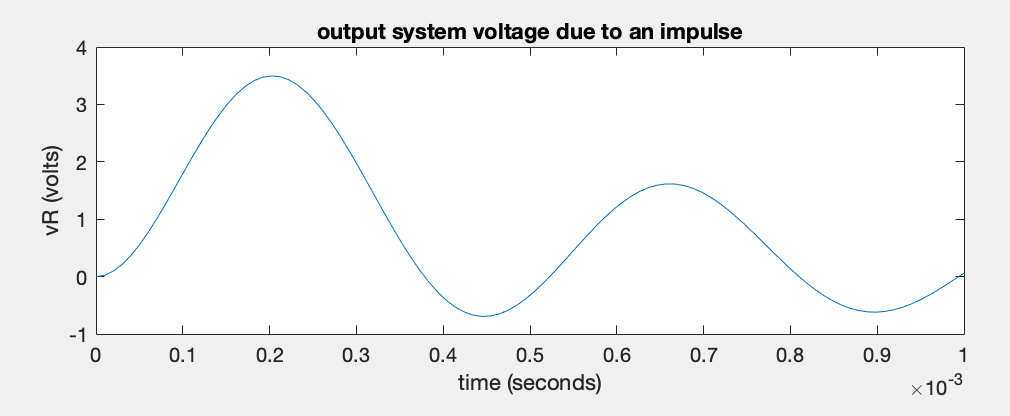
s-domain:
 |
(303) |
Solving the second equation for  , we get
, we get
 |
(304) |
Substituting into the first equation, we get
![$\displaystyle [(R+sL)(1+LC s^2)+sL]V_C(s)=(R+sL)V_s(s)$](img844.svg) |
(305) |
Solving for  we get
we get
 |
(306) |
and
 |
(307) |
The voltage
![$v_R(t)={\cal L}^{-1}[\;V_R(s)\;]$](img847.svg) can be found
by inverse Laplace transform.
can be found
by inverse Laplace transform.















 :
:
 , where
, where


![$\displaystyle \frac{d}{dt}\left[\begin{array}{c}v_R\\ v_C\\ i_C\end{array}\righ...
... i_C\end{array}\right]
+\left[\begin{array}{c}0\\ 0\\ v_s/L_1\end{array}\right]$](img830.svg)


 and an
input
and an
input
![${\bf x}(t)=[0,\;0,\;10^{-3}\delta(t)/L_1]^T$](img834.svg) , we can get
, we can get
![$\displaystyle v_R=[1\;0\;0]{\bf y}=e^{{\bf A}t}
\left[\begin{array}{c}0\\ 0\\ 10^{-3}/L_1\end{array}\right]$](img835.svg)

 and
and
![${\bf V}=[{\bf v}_1,\;{\bf v}_2,\;{\bf v}_3]$](img838.svg) being the eigenvalue
and eigenvector matrices of
being the eigenvalue
and eigenvector matrices of  satisfying
satisfying
 , i.e.,
, i.e.,
 .
.


 , we get
, we get

![$\displaystyle [(R+sL)(1+LC s^2)+sL]V_C(s)=(R+sL)V_s(s)$](img844.svg)
 we get
we get


![$v_R(t)={\cal L}^{-1}[\;V_R(s)\;]$](img847.svg) can be found
by inverse Laplace transform.
can be found
by inverse Laplace transform.