Maximal Margin and Support Vectors

MIT video

Stanford video

The support vector machine (SVM) is a supervised binary classifier trained by a dsta set $\{ ({\bf x}_n, y_n),\;\;n=1,\cdots,N\}$ of which data sample ${\bf x}_n$, a vector in the d-dimensional feature space, belongs to either class $C_+$ if labeled by $y_n=1$ or class $C_-$ if labeled by $y_n=-1$. The result of the training process is the decision boundaries or decision plane $H_0$ in the feature space, described by the linear decision equation:

$$f({\bf x})={\bf w}^T{\bf x}+b=\sum_{i=1}^d x_i w_i+b=0$$ (62)

in terms of its normal vector ${\bf w}$ and intercept $b$. Once the two parameters ${\bf w}$ and $b$ are determined based on the training set, any unlabeled sample ${\bf x}$ can be classified into either of the two classes:

$$\;\;f({\bf x})={\bf w}^T{\bf x}+b\; \left\{ \begin{array}{l} >0 \\ =0\\ <0\end{array} \right., \;\;\; \;\; \left\{ \begin{array}{l} {\bf x}\in C_+ \\ {\bf x}\in H_0\\ {\bf x}\in C_-\end{array} \right.$$ (63)

The initial setup of the SVM algorithm seems the same as the method of linear regression as a linear binary classifier when the linear regression function $f({\bf x})={\bf w}^T{\bf x}+b$ is thresholded by zero to become $f({\bf x})=0$. But here for the SVM, the parameters ${\bf w}$ and $b$ are determined in such a way that the corresponding decision plane separates the training samples belonging to the two classes optimally, so that its distance to the closest samples on either side, called support vectors, is maximized. Also, as kernel mapping can be applied to the SVM, it can also be used for nonlinear classification.

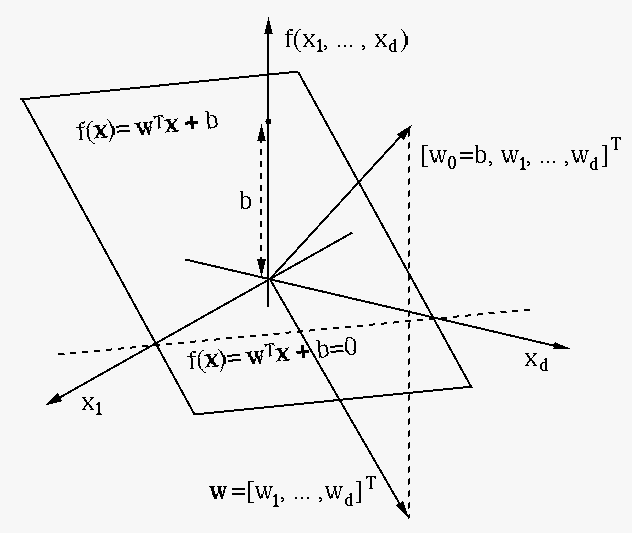
We rewrite the decision equation $f({\bf x})={\bf w}^T{\bf x}+b=0$ as

$$p_{\bf w}({\bf x})=\frac{{\bf w}^T{\bf x}}{\vert\vert{\bf w}\vert\vert} =-\frac{b}{\vert\vert{\bf w}\vert\vert}$$ (64)

and realize this is the projection of any point ${\bf x}\in H_0$ on the decision plane $H_0$ onto its normal direction ${\bf w}$, of which the absolute value is the distance between $H_0$ and the origin:

$$d(H_0,\,{\bf0})=\vert p_{\bf w}({\bf x})\vert=\frac{\vert b\vert}{\vert\vert{\bf w}\vert\vert}$$ (65)

We further find the projection of any point ${\bf x}'\notin H_0$ off the decision plane $H_0$ onto ${\bf w}$ as $p_{\bf w}({\bf x}')={\bf w}^T{\bf x}'/\vert\vert{\bf w}\vert\vert$, and its distance to $H_0$ as:

$$d(H_0,\,{\bf x}')=\bigg\vert p_{\bf w}({\bf x}')-p_{\bf w}({\bf x... ...t{\bf w}\vert\vert} =\frac{\vert f({\bf x}')\vert}{\vert\vert{\bf w}\vert\vert}$$ (66)

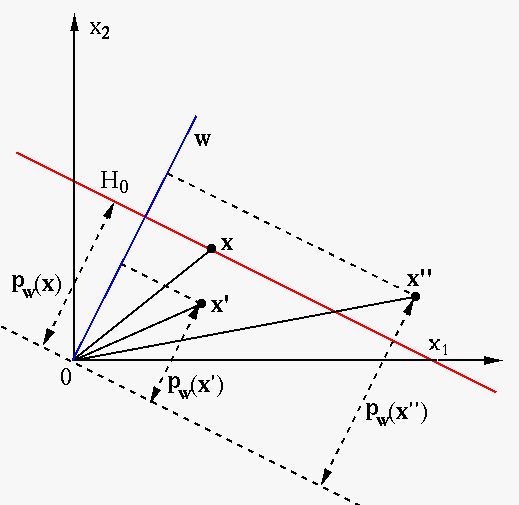
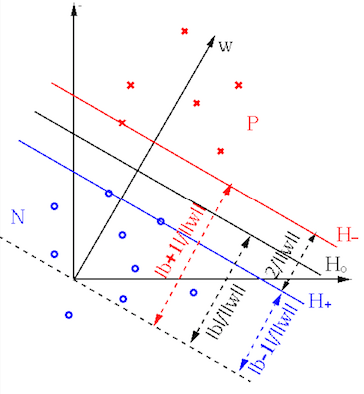
We desire to find the optimal decision plane $H_0$ that separates the training samples belonging to the two different classes, assumed to be linearly separable, in such a way that its distance to the support vectors, denoted by ${\bf x}_{sv}$, is maximized:

$$d(H_0,\,{\bf x}_{sv}\in C_+)=d(H_0,\,{\bf x}_{sv}\in C_-) =d(H_0,\,{\bf x}_{sv})=\frac{\vert f({\bf x}_{sv})\vert}{\vert\vert{\bf w}\vert\vert}$$ (67)

We further consider two additional planes $H_+$ and $H_-$ that are in parallel with $H_0$ and pass through the support vectors ${\bf x}_{sv}$ on either side of $H_0$:

$$f_{\pm}({\bf x})=f({\bf x})\pm c={\bf w}^T {\bf x}+b\pm c ={\bf w}^T {\bf x}+b\pm 1=0$$ (68)

As these equations can be arbitrarily scaled, we can let $c=1$ for convenience. Based on Eq. (65), the distances from $H_+$ or $H_-$ to the origin can be written as

$$d(H_{\pm},{\bf0})=\frac{\vert b\pm c\vert}{\vert\vert{\bf w}\vert\vert} =\frac{\vert b\pm 1\vert}{\vert\vert{\bf w}\vert\vert}$$ (69)

and their distances to the decision plane $H_0$, called the decision margin, can be found as:

$$d(H_\pm,H_0)= \bigg\vert d(H_\pm,{\bf0})-d(H_0,{\bf0}) \bigg\vert... ...ert c\vert}{\vert\vert{\bf w}\vert\vert} =\frac{1}{\vert\vert{\bf w}\vert\vert}$$ (70)

To maximize this margin, we need to minimize $\vert\vert{\bf w}\vert\vert$.

For these planes to correctly separate all samples in the training set $\{({\bf x}_n,\,y_n)\;\;(n=1,\cdots,N)\}$, they have to satisfy the following two conditions:

$$\left\{\begin{array}{ll} f_-({\bf x}_n)={\bf w}^T {\bf x}_n+b-1 \... ...+b+1 \le 0 & \mbox{if $y_n=-1$} \end{array}\right. \;\;\;\;\;\;\;(n=1,\cdots,N)$$ (71)

where the equality is satisfied by the support vectors on $H_+$ or $H_-$, while the inequalities are satisfied by all other samples farther away from $H_0$ behind $H_+$ or $H_-$. The two conditions above can be combined to become:

$$y_n ({\bf w}^T{\bf x}_n +b) \ge 1,\;\;\;\;\;\;(n=1,\cdots,N)$$ (72)

Now the task of finding the optimal decision plane $H_0$ can be formulated as a constrained minimization problem:

$$\;\; \frac{1}{2}\vert\vert{\bf w}\vert\vert^2 =\frac{1}{2}{\bf w}^T {\bf w}$$

$$\;\; y_n ({\bf x}_n^T {\bf w}+b) \ge 1,\;\;\;\;(n=1,\cdots,N)$$ (73)

Example:

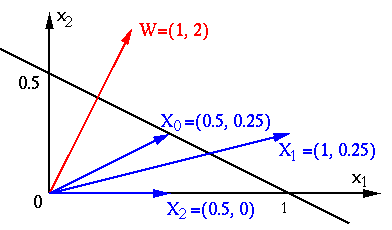
The straight line in 2D space shown above, denoted by $H_0$, is described by the following linear equation

$$f({\bf x})={\bf w}^T{\bf x}+b=[w_1,w_2] \left[ \begin{array}{c} x... ...b =[1, 2]\left[ \begin{array}{c} x_1 \\ x_2 \end{array} \right]-1 =x_1+2x_2-1=0$$ (74)

The distance from $H_0$ to the origin is:

$$d(H_0,{\bf0})=\frac{\vert b\vert}{\vert\vert{\bf w}\vert\vert}=\frac{1}{\sqrt{w_1^2+w_2^2}} =\frac{1}{\sqrt{1^2+2^2}}=\frac{1}{\sqrt{5}}=0.447$$ (75)

which is invariant with respect to any scaling of the equation. Consider three points in the space:

• ${\bf x}_0=[0.5,\;0.25]^T$, $f({\bf x}_0)=0.5+2\times 0.25-1=0$, i.e., ${\bf x}_0$ is on the plane. Its distance to the plane is $d({\bf x}_0,H)=f({\bf x}_0)/\vert\vert{\bf w}\vert\vert=0$.
• ${\bf x}_1=[1,\;0.25]^T$, $f({\bf x}_1)=1+2\times 0.25-1=0.5>0$, i.e., ${\bf x}_1$ is above the straight line, its distance to the plane is $d({\bf x}_1,H)=f({\bf x}_1)/\vert\vert{\bf w}\vert\vert=\vert.5\vert/\sqrt{5}=0.2235$.
• ${\bf x}_2=[0.5,\;0]^T$, $f({\bf x}_2)=0.5+2\times 0-1=-0.5<0$, i.e., ${\bf x}_2$ is below the straight line, its distance to the plane is $d({\bf x}_2,H)=f({\bf x}_2)/\vert\vert{\bf w}\vert\vert=\vert-0.5\vert/\sqrt{5}=0.2235$.

These two points ${\bf x}_1=[1,\,0.25]^T$ and ${\bf x}_2=[0.5,\,0]^T$ with equal distance to $H_0$, the straight line $f({\bf x})=x_1+2x_2-1=0$, can be assumed to be two support vectors ${\bf x}_{sv}$ on either side of $H_0$, and

$$\vert f({\bf x}_{sv})\vert=\vert{\bf w}^T{\bf x}_1+b\vert=\vert{\bf w}^T{\bf x}_2+b\vert=0.5$$ (76)

Multiplying $2$ on both sides of the decision equation $f({\bf x})=0$, it is scaled to become

$$f({\bf x})={\bf w}^T{\bf x}+b=2x_1+4x_2-2=0$$ (77)

and the two equations diescribing $H_+$ parallel to $H_0$ and passing through ${\bf x}_1$ and $H_-$ passing through ${\bf x}_2$ are

$$H_+: 2x_1+4x_2-2-1=2x_1+4x_2-3=0$$

$$H_-: 2x_1+4x_2-2+1=2x_1+4x_2-1=0 \nonumber$$

Their distances to the origin are

$$d(H_+,\,{\bf0})=\frac{\vert-3\vert}{\vert\vert{\bf w}\vert\vert}=... ...\;\;\;\; d(H_-,\,{\bf0})=\frac{\vert-1\vert}{\vert\vert{\bf w}\vert\vert}=0.447$$ (78)

and the distance between $H_-$ and $H_+$ is indeed $2/\vert\vert{\bf w}\vert\vert$:

$$d(H_-,\,H_+)=d(H_+,\,{\bf0})-d(H_-,\,{\bf0})=\frac{2}{\vert\vert{\bf w}\vert\vert} =0.894$$ (79)

twice the distance between $H_0$ and the origin $d(H_0,{\bf0})=0.447$ found previously.

For reasons to be discussed later, instead of directly solving the constrained minimization problem in Eq. (73), now called the primal problem, we actually solve the dual problem. Specifically, we first construct the Lagrangian function of the primal problem:

$$L_p({\bf w},b,{\bf\alpha})=\frac{1}{2}{\bf w}^T{\bf w} +\sum_{n=1}^N \alpha_n(1-y_n( {\bf w}^T {\bf x}_n+b))$$ (80)

where $\alpha_1,\cdots,\alpha_N$ are the Lagrange multipliers, which is called the primal function. Here for this minimization problem with non-positive constraints, the Lagrangian multipliers are required to be negative, $\alpha_n$, according to Table here, if a minus sign is used for the second term. However, to be consistent with most SVM literatures, we use the positive sign for the second term and require $\alpha_n\ge 0$. Note that if ${\bf x}_n$ is a support vector on either $H_+$ or $H_-$, i.e., the equality constraint $y_n({\bf w}^T{\bf x}_n+b)=1$ holds, then $\alpha_n>0$; but if ${\bf x}_n$ is not a support vector, the equality constraint does not hold, and $\alpha_n=0$.

We next find the minimum (or infimum) as the lower bound of the primal function $L_p({\bf w},b)$ in Eq. (80), by setting to zero its partial derivatives with respect to both $b$ and ${\bf w}$:

$$\frac{\partial}{\partial b}L_p({\bf w},b) =\frac{\partial}{\parti... ...}^N \alpha_n(1-y_n( {\bf w}^T {\bf x}_n+b))\right] =\sum_{n=1}^N \alpha_n y_n=0$$ (81)

and

$$\frac{\partial}{\partial {\bf w}}L_p({\bf w},b) =\frac{\partial}{... ...\bf w}^T {\bf x}_n+b))\right] ={\bf w}-\sum_{n=1}^N\alpha_ny_n{\bf x}_n={\bf0},$$ (82)

i.e.,

$${\bf w}=\sum_{n=1}^N \alpha_n y_n {\bf x}_n$$ (83)

Substituting these back into the primal function $L_p({\bf w},b,{\bf\alpha})$, we get its lower bound as a function of the Lagrange multipliers $\{\alpha_1,\cdots,\alpha_N\}$, called the dual function:

$$L_d({\bf\alpha}) = \inf_{{\bf w},b} L_p({\bf w},b,{\bf\alpha}) =\inf_{{\bf w},b}\lef... ...}{\bf w}^T{\bf w} +\sum_{n=1}^N \alpha_n(1-y_n( {\bf w}^T {\bf x}_n+b)) \right]$$

$$= \inf_{{\bf w},b}\left[\frac{1}{2}{\bf w}^T{\bf w} +\sum_{n=1}^N \... ...\bf w}^T \sum_{n=1}^N \alpha_ny_n{\bf x}_n -b\;\sum_{n=1}^N \alpha_ny_n \right]$$

$$= \frac{1}{2} \left(\sum_{m=1}^N \alpha_m y_m {\bf x}_m\right)^T \l... ...alpha_m y_m {\bf x}_m\right)^T \left(\sum_{n=1}^N \alpha_n y_n {\bf x}_n\right)$$

$$= \sum_{n=1}^N\alpha_n -\frac{1}{2} \sum_{n=1}^N \sum_{m=1}^N \alpha_n \alpha_m y_n y_m \left({\bf x}_n^T{\bf x}_m\right)$$ (84)

To further find the greatest or tightest lower bound of the primal function, we need to maximize this dual function $L_d({\bf\alpha})$ with respect to the Lagrange multipliers, subject to the constraint imposed by Eq. (81):

$$\;\; L_d({\bf\alpha}) =\sum_{n=1}^N\alpha_n -\frac{1}{2} \sum_{n=1}^N ... ...bf x}_m\right) ={\bf 1}^T{\bf\alpha}-\frac{1}{2}{\bf\alpha}^T{\bf Q}{\bf\alpha}$$

$$\;\; \sum_{n=1}^N \alpha_n y_n ={\bf y}^T{\bf\alpha}=0, \;\;\;\; \alpha_n\ge 0\;\;\;(n=1,\cdots,N)$$ (85)

where ${\bf Q}$ is an $N$ by $N$ symmetric matrix of which the component in the mth row and nth column is $Q(m,n)=y_my_n{\bf x}_m^T{\bf x}_n$ ( $m,n=1,\cdots,N$). Now we have converted the primal problem of constrained minimization of the primal function $L_p({\bf w},b,{\bf\alpha})$ with respect to ${\bf w}$ and $b$ to its dual problem of linearly constrained maximization of the dual function $L_d({\bf\alpha})$ with respect to $\{\alpha_1,\cdots,\alpha_N\}$. Solving this quadratic programming (QP) problem, we get all Lagrange multipliers $\alpha_n\ge 0,\;(n=1,\cdots,N)$. All training samples ${\bf x}_n$ corresponding to positive Lagrange multipliers $\alpha_n>0$ are support vectors, while others corresponding to $\alpha_n=0$ are not support vectors.

We can now find the normal direction ${\bf w}$ of the optimal decision plane based on Eq. (83):

$${\bf w}=\sum_{n=1}^N \alpha_n y_n {\bf x}_n =\sum_{n\in sv} \alph... ...C_+,\;n\in sv} \alpha_n{\bf x}_n -\sum_{x_n\in C_-,\;n\in sv} \alpha_n{\bf x}_n$$ (86)

Note that the normal vector ${\bf w}$ is the difference between the weighted means of the support vectors in class $C_+$ (first term) and class $C_-$ (second term), and it is determined only by the support vectors.

Having found $\{\alpha_1,\cdots,\alpha_N\}$, we can also find $b$ based on the equality of Eq. (72) for any of the support vectors:

$$y_n \left( {\bf w}^T {\bf x}_n+b\right) = 1\;\;\;\;\; \;\;\;\; {\bf w}^T {\bf x}_n+b = y_n,\;\;\;\;\;\;(n\in sv)$$ (87)

(recall $y_n^2=1$). Solving the equation for $b$ we get:

$$b = y_n-{\bf w}^T {\bf x}_n =y_n-\sum_{m \in sv} \alpha_m y_m( {\bf x}_m^T{\bf x}_n),\;\;\;\;\;(n\in sv)$$ (88)

All support vectors should yield the same result. Computationally we simply get $b$ as the average of the above for all support vectors.

We note that both ${\bf w}$ and $b$ depend only on the support vectors on planes $H_+$ and $H_-$, corresponding to a positive $\alpha_n>0$, while all remaining samples corresponding to $\alpha_n=0$ are farther away from the decision plane $H_0$, behind either $H_+$ or $H_-$. We see that the SVM is solely based on those support vectors in the training set, once they are identified during the training process, all other non-support vectors are irrelevant.

Having obtained ${\bf w}$ and $b$ as shown above as the training process, any unlabeled sample ${\bf x}$ can be classified into either of the two classes depending on whether the following decision function is greater or smaller than zero:

$$f({\bf x})={\bf w}^T{\bf x}+b =\left(\sum_{n\in sv}\alpha_ny_n{\b... ...\{\begin{array}{ll}>0 & {\bf x}\in C_+\\ <0 & {\bf x}\in C_- \end{array}\right.$$ (89)

We also get:

$$\vert\vert{\bf w}\vert\vert^2 = {\bf w}^T {\bf w} =\left(\sum_{n\in sv} \alpha_n y_n {\bf x}^T_n\... ...=\sum_{n\in sv} \alpha_n y_n \sum_{m\in sv} \alpha_m y_m ({\bf x}^T_n{\bf x}_m)$$

$$= \sum_{n\in sv} \alpha_n y_n (y_n-b)=\sum_{n\in sv} \alpha_n (1-y_... ...=\sum_{n\in sv} \alpha_n - b\sum_{n\in sv} \alpha_n y_n=\sum_{n\in sv} \alpha_n$$ (90)

The last equality is due to equality constraints of the dual problem $\sum_{n=1}^N \alpha_n y_n=0$. Now the decision margin can be written as:

$$\frac{1}{\vert\vert{\bf w}\vert\vert}=\left(\sum_{n\in sv} \alpha_n\right)^{-1/2}$$ (91)

The SVM algorithm for binary classification can now by summarized as the following steps:

• Find the Lagrange multipliers $\{\alpha_1,\cdots,\alpha_N\}$ by solving the QP problem in Eq. (85);
• Find the normal vector ${\bf w}$ by Eq. (86);
• Find the bias $b$ by Eq. (88);
• Classify unlabeled ${\bf x}$ by Eq. (89).

As the last expression of the decision function in Eq. (89) depends only on $\alpha_n$ as well as ${\bf x}_n$ and $y_n$ in the training set, the normal vector ${\bf w}$ is never needed, and the second step above for calculating ${\bf w}$ by Eq. (86) can be dropped.

We prefer to solve this dual problem not only because it is easier than the original primal problem, but also, more importantly, for the reason that all data points appear only in the form of an inner product ${\bf x}_n^T{\bf x}_m$ in the dual problem, allowing the kernel method to be used, as discussed later.

The Matlab code for the essential part of the algorithm is listed below, where X and y are respectively the data array composed of $N$ training vectors $[{\bf x}_1,\cdots,{\bf x}_N]$ and their corresponding labelings $y_1,\cdots,y_N$, and IPmethod is a function that implements the interior point method for solving a general QP problem of minimizing ${\bf x}^T{\bf Qx}/2+{\bf c}^T{\bf x}$ subject to the linear equality constraints ${\bf Ax}={\bf b}$ and ${\bf x}\ge {\bf0}$.

    [X y]=getData;               % get the training data
    [m n]=size(X);   
    Q=(y'*y).*(X'*X);            % compute the quadratic matrix
    c=-ones(n,1);                % coefficients of linear term
    A=y;                         % coefficient matrix and 
    b=0;                         % constants of linear equality constraints
    alpha=0.1*ones(n,1);         % initial guess of solution

    [alpha mu lambda]=IPmethod(Q,A,c,b,alpha);  % solve QP to find alphas
                                                % by interior point method
    I=find(abs(alpha)>10^(-3));  % indecies of non-zero alphas
    asv=alpha(I);                % non-zero alphas
    Xsv=X(:,I);                  % support vectors
    ysv=y(:,I);                  % their labels
    w=sum(repmat(ysv.*asv,m,1).*Xsv,2);  % normal vector (not needed)
    bias=mean(ysv-w'*Xsv);               % bias

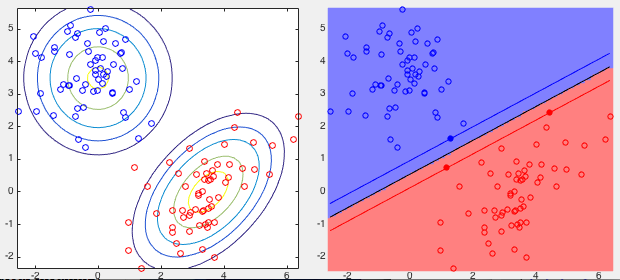
Example: The training set contains two classess of 2-D points with Gaussian distributions generated based on the following mean vectors and covariance matrices:

$${\bf m}_-=\left[\begin{array}{c}3.5\\ 0\end{array}\right],\;\;\;\... ...y}\right],\;\;\;\; {\bf S}_+=\left[\begin{array}{cc}1&0\\ 0&1\end{array}\right]$$ (92)

The SVM algorithm finds the weight vector ${\bf w}$ and constant $b$ of the optimal boundary between the two classes based on three support vectors, all listed below. Note that decision boundary is completely dictated by the three support vectors and the margion distance between them is maximized.

$$\begin{array}{c\vert c\vert l\vert r}\hline n & \alpha_n & {\... ...rray}{r}-1.25\\ 2.39\end{array}\right],\;\;\;\;\;\;\;\; b=-1.31$$ (93)