Linear Regression Based on Basis Functions

The method of linear regression considered previously can be generalized to model nonlinear relationships between the dependent variable $y$ and the independent variables in ${\bf x}=[x_1,\cdots,x_d]^T$ by a regression function as a linear combination of $K$ nonlinear basis functions of ${\bf x}$:

$$\hat{y}=f({\bf x}) =\sum_{k=1}^K w_k \,\varphi_k({\bf x},{\bf\theta})$$ (145)

where $\varphi_k({\bf x},{\bf\theta}),\;(k=1,\cdots,K)$ is the basis functions parameterized by ${\bf\theta}$ that span the function space in which $\hat{y}$ resides. Some of the common basis functions include the following:

• Power function:

  $$\varphi_k(x)=x^{k-1}$$ (146)

  The regression function $f(x)$ is $(K-1)$th order polynomial function.

• Sinusoidal function:

  $$\varphi_k(x,\omega)=\sin((k-1)\omega x), \;\;\;\; \;\;\;\;\; \varphi_k(x,\omega)=\cos((k-1)\omega x)$$ (147)

  The regression function $f(x)$ is similar to the sine or cosine series expansion of the given function.

• Gassian function:

  $$\varphi_k({\bf x},{\bf c}_k)=\exp(a \vert\vert{\bf x}-{\bf c}_k\vert\vert^2)$$ (148)

  The is function is one member of a family of functions called radial basis functions (RBFs), all of which are centered at point ${\bf c}_k$.

• Sigmoid function:

  $$\varphi_k({\bf x},{\bf c}_k,a)=\frac{1}{1+e^{-a\vert\vert{\bf x}-{\bf c}_k\vert\vert}}$$ (149)

These four types of basis functions are show below:

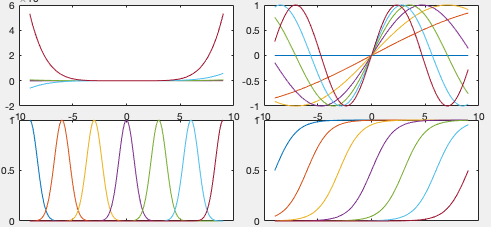
The original d-dimensional data space spanned by $x_1,\cdots,x_d$ is now converted to a K-dimensional space spanned by the $K$ basis functions $\varphi_1({\bf x}),\cdots,\varphi_K({\bf x})$. Applying such a regression model to each data point ${\bf x}_n$, we get

$$\hat{y}_n=\sum_{k=1}^K w_k \,\varphi_k({\bf x}_n) \;\;\;\;\;\;(n=1,\cdots,N)$$ (150)

or in matrix form:

$$\hat{\bf y} =\left[\begin{array}{c}y_1\\ \vdots\\ y_N\end{array}\... ... \left[\begin{array}{c}w_1\\ \vdots\\ w_K\end{array}\right] ={\bf\Phi}^T{\bf w}$$ (151)

where ${\bf\Phi}$ is a $K\times N$ matrix of which the component in the nth row and kth column is the kth basis function evaluated at the nth data point:

$${\bf\Phi}=\left[\begin{array}{ccc} \varphi_1({\bf x}_1)&\cdots&\v... ...ts&\vdots\\ \varphi_1({\bf x}_N)&\cdots&\varphi_K({\bf x}_N)\end{array}\right]$$ (152)

Typically there are many more sample data points than the basis functions, i.e., $N\gg K$.

As the nonlinear model $\hat{\bf y}={\bf\Phi}^T{\bf w}$ in Eq. (151) is in the same form as the linear model $\hat{\bf y}={\bf X}^T{\bf w}$ in Eq. (108), we can solve it to find the LS solution ${\bf w}^*$ the same way as in Eq. (116), by simply replacing ${\bf X}$ by ${\bf\Phi}$:

$${\bf w}^*=({\bf\Phi\Phi}^T)^{-1}{\bf\Phi}{\bf y} =({\bf\Phi}^T)^-{\bf y}$$ (153)

where $({\bf\Phi}^)^^-=({\bf\Phi\Phi}^T)^{-1}{\bf\Phi}$ is the $K\times N$ pseudo-inverse of the $N\times K$ matrix ${\bf\Phi}^T$. Now we get the output of the regression model

$$\hat{\bf y}={\bf\Phi}^T{\bf w}={\bf\Phi}^T{\bf\Phi}^-{\bf y} ={\bf\Phi}^T({\bf\Phi\Phi}^T)^{-1}{\bf\Phi}{\bf y}$$ (154)

The Matlab code segment belows shows the essential part of the algorithm, where $x(n)$ is the nth data sample ${\bf x}_n$ out of the total of $N$, $y(x)$ represents vector ${\bf y}=[y_1,\cdots,y_N]^T$ with $y_n=f({\bf x}_n)$, and $c(k)$ represents the parameters for the kth basis function $\phi({\bf x},c(k))$.

     for n=1:N
         for k=1:K
             Phi(n,k)=phi(x(n),c(k));   
         end
     end
     w=pinv(Phi)*y(x);    	% weight vector by LS method
     yhat=Phi*w;                % reconstructed function

Example:

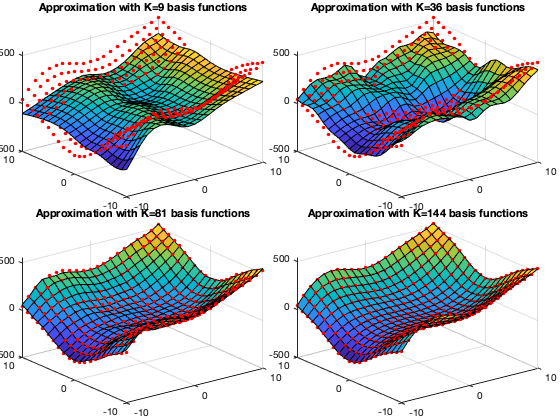
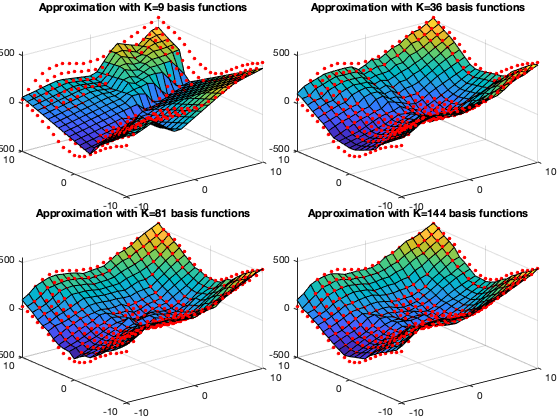
The plots below show the approximations of a function using linear regression based on four different types of basis functions listed above. We see that the more basis functions are used, the more accurately the given funtion is approximated.

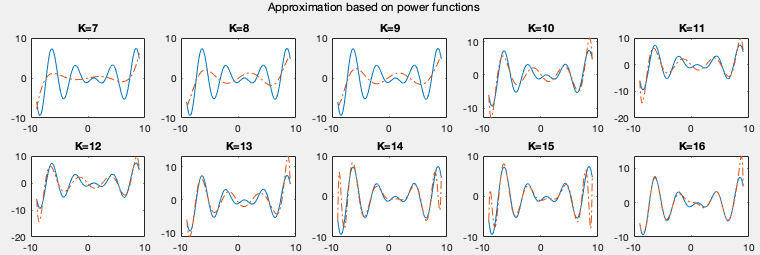
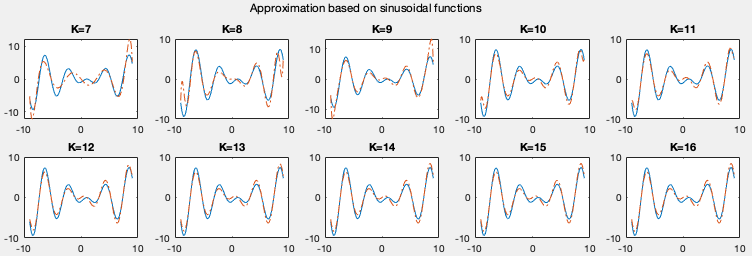
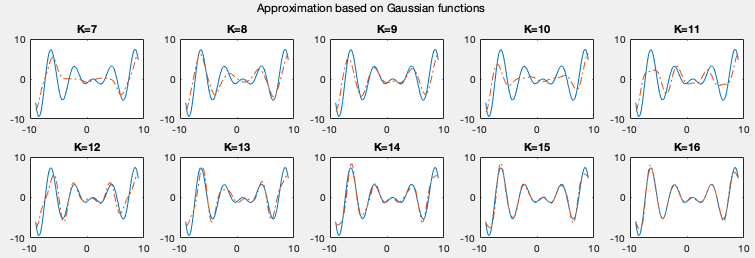
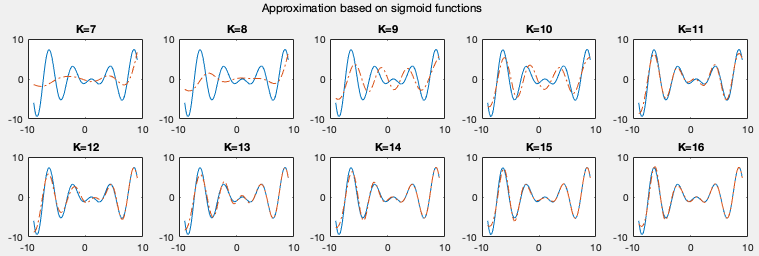
Example:

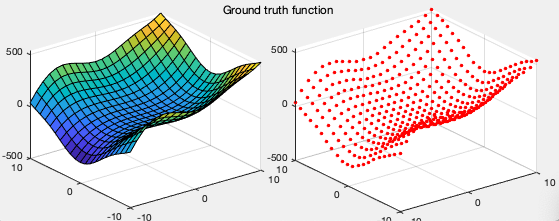
The plots below show the approximations of a 2-D function $f({\bf x})=f(x_1,\,x_2)$ shown below using linear regression based on Gaussian basis functions centered at $K$ different locations in the 2-D space.

The figure below shows a 2-D function (left) and the $N$ sample points (right) used for regression:

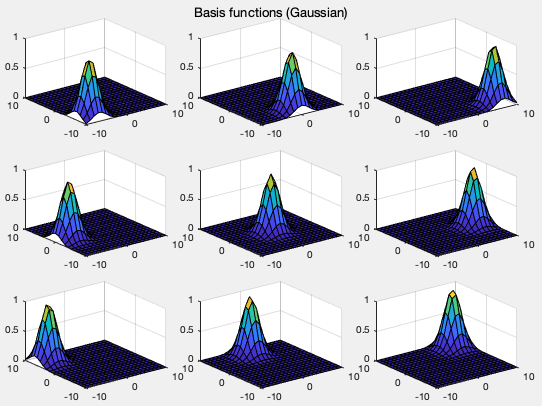
The figure below shows $K=9$ Gaussian basis functions located at different locations in the 2-D space:

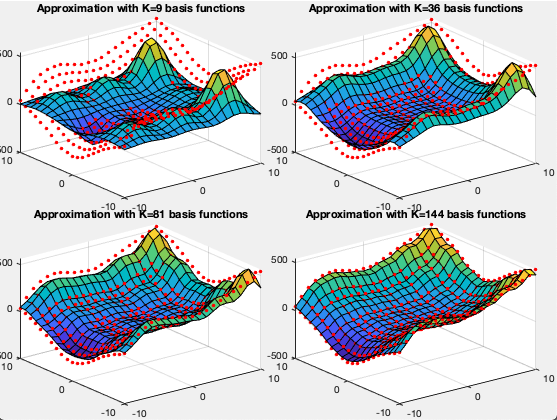
The figure below shows the approximated functions based on different number $K$ of basis functions:

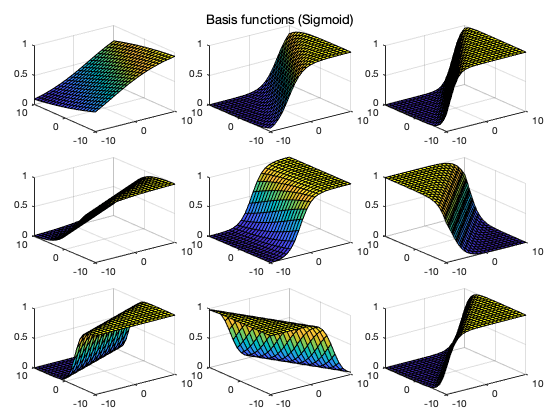
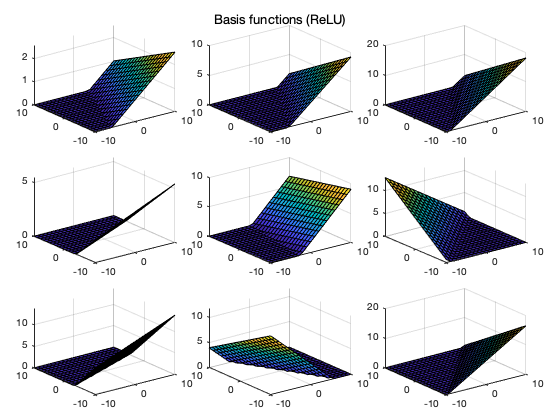
In addition to the different types of basis functions listed above, we further consider the following basis functions:

$$\varphi_k({\bf x},{\bf w}_k,b_k) =g\left({\bf w}_k^T{\bf x}+b_k\r... ...=g\left(\sum_{i=1}^d w_{dk}x_d+b_k\right) =g\left(\sum_{i=0}^d w_{dk}x_d\right)$$ (155)

where $g(x)$ in, called activation function, can take some different forms such as

$$g(x)=\left\{\begin{array}{ll} 1/(1+e^{-x}) & \mbox{sigmoid functi... ...ge 0\end{array}\right. & \mbox{rectified linear unit (ReLU)} \end{array}\right.$$ (156)

The regression method based on these basis functions can be interpreted as a three-layer neural network shown below, containing the input layer, the middle and hidden layer and the output layer of multiple units, called neurons or nodes.

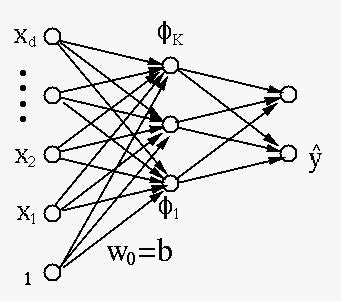
As shown in figure, the $d$ nodes of the input layer take the $d$ components of one of the data points ${\bf x}_n$ as inputs, and each of the $K$ nodes of the hidden layer finds the linear combination ${\bf w}_k^T{\bf x}$ of these $d$ components from the input layer together with a bias term $b_k$, and generates an output $\varphi_k({\bf x})=g\left({\bf w}_k^T{\bf x}+b_k\right)$. A node of the output layer in tern takes the outputs from the $K$ nodes in the hidden layer and generates an output $\hat{y}=\hat{f}({\bf x}_n)=\sum_{k=1}^Kw_k\varphi_k({\bf x}_n)$ as the regression approximation of the desired function $f({\bf x}_n)$. Note that there exist two sets of weights here, those in vector ${\bf w}_k$ for each of the $K$ hidden layer nodes, and those for the node of the output layer found in Eq. (153). If there are multiple nodes in the output layer, they can each approximate a different function. This three-layer network is of particular interest in neural network algorithms, to be considered in Chapter 9. ///

Example

This method of regression based on basis functions is applied to approximating the same 2-D function $f({\bf x})=f(x_1,\,x_2)$ in the previous example, as a linear combination of $K$ basis functions $\varphi_k({\bf x})={\bf w}_k^T{\bf x}+b_k$ with each parameterized by ${\bf w}_k$ and $b_k$. The regression is based on a set of $N$ data samples $\{ {\bf x}_1,\cdots,{\bf x}_N\}$ taken from a grid of the 2-D space, and the corresponding function values in $\{y_1,\cdots,y_N\}$.

The Matlab code segment below shows the essential part of the program for this example, where $f$ is a function to be approxmiated, which can be arbitrarily specified.

    g=@(x) x.*(x>0);        % ReLU activation function, or
    g=@(x) 1/(1+exp(-x));   % Sigmoid activation function
    g=@(x,w,b)g(w'*x+b);    % the basis function
    
    [X,Y]=meshgrid(xmin:1:xmax, ymin:1:ymax); % define 2-D points
    nx=size(X,2);           % number of samples in first dimension
    ny=size(Y,1);           % number of samples in second dimension
    N=nx*ny;                % total number of data samples
    Phi=zeros(N,K);   	    % K basis functions evaluated at N sample points
    W=1-2*rand(2,K);        % random initialization of weights
    b=1-2*rand(1,K);        % and biases for K basis functions
    n=0;
    for i=1:nx
        x(1)=X(1,i);        % first component 
        for j=1:ny
            x(2)=Y(j,1);    % second component
            n=n+1;          % of the nth sample
            Y(i,j)=func(x); % function evalued at the sample
            for k=1:K       % basis functions evaluated at the sample
                Phi(n,k)=g(x,W(:,k),b(k));
            end
        end
    end
    y=reshape(Y,N,1);       % convert function values to vector
    w=pinv(Phi)*y;    	    % find weights by LS method
    yhat=Phi*w;             % reconstructed function 
    Yhat=reshape(yhat,m,n); % convert vector y to 2-D to compare w/ Y

The figures below show the regression results as well as the basis functions used, based on both the sigmoid and ReLU activation functions. We note that as the function is better approximated when more basis functions are used in the regression.

• Regression based on sigmoid function:

  

• Regression based on ReLU function: