Solving First Order ODEs

Only in the special case of LCCODE, can the equation be solved analytically to obtain a closed-form solution as discussed above. In the general case of nonlinear ODE systems, the closed-form solutions no longer exist, and we can only solve such an equation numerically based on a given initial condition $y(0)=y_0$.

We first consider solving a first order ODE which can be written in the explicit form:

$$y'(t)=\frac{d}{dt}y(t)=f(t,y(t))$$ (179)

This ODE can be solved iteratively, by estimating its next value $y(t+h)$ from the previous one $y(t)$:

$$y(t+h) = y(t)+\Delta y=y(t)+h\,\frac{y(t+h)-y(t)}{h}$$

$$= y(t)+h\, y'(t+ch)=y(t)+h\; f(t+ch,\,y(t+ch))$$ (180)

where $h$ is the step size, $\Delta y=y(t+h)-y(t)$, $c$ is a value between 0 and $1$, and

$$\frac{\Delta y}{h}=\frac{y(t+h)-y(t)}{h} =y'(t+ch),\;\;\;\;\;\;\;(0\le c\le 1)$$ (181)

is the slope of the secant of the function $y(t)$ through the two $y(t)$ and $y(t+h)$, which, according to the mean value theorem, is equal to the derivative of the function at some point $t+ch$ inside the interval $[t,\;t+h]$.

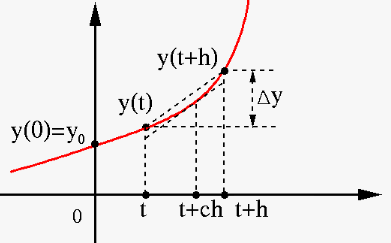
However, as the slope $y'(t+ch)$ of the secant is unknown, all methods considered below approximate $y(t+h)$ from $y(t)$ based on certain estimated slope of the secant between $y(t)$ and $y(t+h)$:

$$y(t+h)\approx \hat{y}(t+h)=y(t)+h\; \hat{y'}(t+ch)$$ (182)

The goal is to minimize the error, represented as a kth power function of the step size $h$:

$$=\vert y(t+h)-\hat{y}(t+h)\vert\propto O(h^k)$$ (183)

As $h<1$ is small, the higher the order $k$ of the error term, the more accurate a method is.

Eq. (180) can be expressed as an iteration:

$$y_{n+1}=y_n+h\,y'(t_n+ch)=y_n+h\,f(t_n+ch, y(t_n+ch))$$ (184)

where $t_n=t$, $t_{n+1}=t+h$, $y_n=y(t_n)=y(t)$, $y_{n+1}=y(t_{n+1})=y(t+h)$, and $f_n=f(t_n,\,y(t_n))$.

We further note that the increment $\Delta y=y(t+h)-y(t)$ in Eq. (180) can also be obtained as an integration based on the given $y'(t)=f(t,y(t))$, by the method of Newton-Cotes quadrature:

$$\Delta y=y(t+h)-y(t)=\int_t^{t+h} y'(\tau)\,d\tau \approx\sum_{i=0}^n c_i y'(t_i)=\sum_{i=0}^n c_i f(t_i,y(t_i))$$ (185)

• $n=1$ trapezoidal rule based on two points:

  $$\int_t^{t+h} y'(\tau)\,d\tau\approx \frac{h}{2}[y'(t)+y'(t+h)] =\frac{h}{2}[f(t,y(t))+f(t+h,y(t+h))]$$ (186)

• $n=2$ Simpson's rule based on three points:
  

  $$\int_t^{t+h} y'(\tau)\,d\tau \approx \frac{h}{6}[y'(t)+4 y'(t+h/2)+y'(t+h)]$$

  $$= \frac{h}{3}[f(t,y(t))+4 f(t+h/2,y(t+h/2))+f(t+h,y(t+h))]$$ (187)

  
  
• $n=3$ Simpson's 3/8 rule based on four points:
  

  $$\int_t^{t+h} y'(\tau)\,d\tau \approx \frac{h}{8}[y'(t)+3y'(t+h/3)+3y'(t+2h/3)+y'(t+h)]$$

  $$= \frac{h}{8}[f(t,y(t))+3f(t+h/3,y(t+h/3))+3f(t+2h/3,y(t+2h/3)) +f(t+h,y(t+h))]$$ (188)

  
  

However, we note that in these equations, function values such $y(t+h/3),\;y(t+h/2),\;y(t+2h/3)$ and $y(t+h)$ are unknown and need to be estimated so that the error is minimized.