Consider a first-order autonomous ODE system containing  equations:
equations:
 or or![$\displaystyle \;\;\;\;\;\;\;\;
\left[\begin{array}{l} y_1'(t)\\ y_2'(t)\end{arr...
...right]
=\left[\begin{array}{l}f_1(y_1,\;y_2)\\ f_2(y_1,\;y_2)\end{array}\right]$](img392.svg) |
(155) |
Note that the system is autonomous as it does not explicitly
depends on the independent variable  . A phase plane plot
can be made to visualize certain properties such as the stability
of the solution. Specifically, let
. A phase plane plot
can be made to visualize certain properties such as the stability
of the solution. Specifically, let  and
and  span a 2-D
plane in which every point is associated with a vector with two
components
span a 2-D
plane in which every point is associated with a vector with two
components
![$\displaystyle {\bf f}=\left[\begin{array}{c}f_1\\ f_2\end{array}\right]
=\left[\begin{array}{c}y'_1\\ y'_2\end{array}\right]$](img395.svg) |
(156) |
represented by an arrow indicating the direction along which the
system is moving as time  progresses. If the vector at a point
is zero
progresses. If the vector at a point
is zero
![$\displaystyle {\bf f}=\left[\begin{array}{l} f_1\\ f_2\end{array}\right]
=\left[\begin{array}{l} 0\\ 0\end{array}\right]={\bf0}$](img396.svg) |
(157) |
then the point is an equalibrium point.
We first consider the special case of LCCODE as an example:
![$\displaystyle {\bf y}'=\left[\begin{array}{c}y_1\\ y_2\end{array}\right]'
=\lef...
... d\end{array}\right]
\left[\begin{array}{c}y_1\\ y_2\end{array}\right]={\bf Ay}$](img397.svg) |
(158) |
Obviously the point  is an equilibrium solution at
which
is an equilibrium solution at
which
 . As the solution of
this homogeneous system is in the following form:
. As the solution of
this homogeneous system is in the following form:
 |
(159) |
we see that this solution is stable if the real parts of all
eigenvalues are smaller than zero. By solving the characteristic
equation of  :
:
where
 and
and
 are the
trace and determinant of
are the
trace and determinant of  respectively, we can get the
eigenvalues of
respectively, we can get the
eigenvalues of 
 |
(161) |
where
 .
.
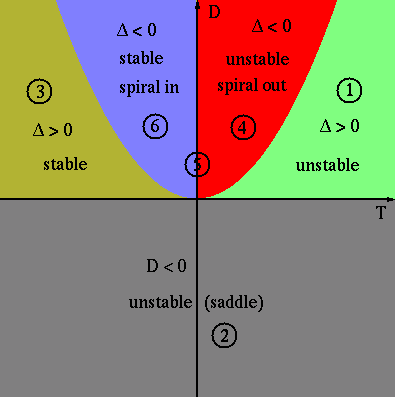
- If
 (above the parabola), i.e.,
(above the parabola), i.e.,
 ,
then
,
then
 are two complex
conjugate roots,
are two complex
conjugate roots,
 |
(162) |
- If
 (between the parabola and horizontal axis),
i.e.,
(between the parabola and horizontal axis),
i.e.,
 , then
, then
 are two real roots,
are two real roots,
 |
(163) |
- If
 (below horizontal axis), i.e.,
(below horizontal axis), i.e.,
 ,
then
,
then
 have opposite signs,
unstable (saddle point);
have opposite signs,
unstable (saddle point);
In summary, the solution is stable only if  and
and  (the
top-left quadrant).
(the
top-left quadrant).
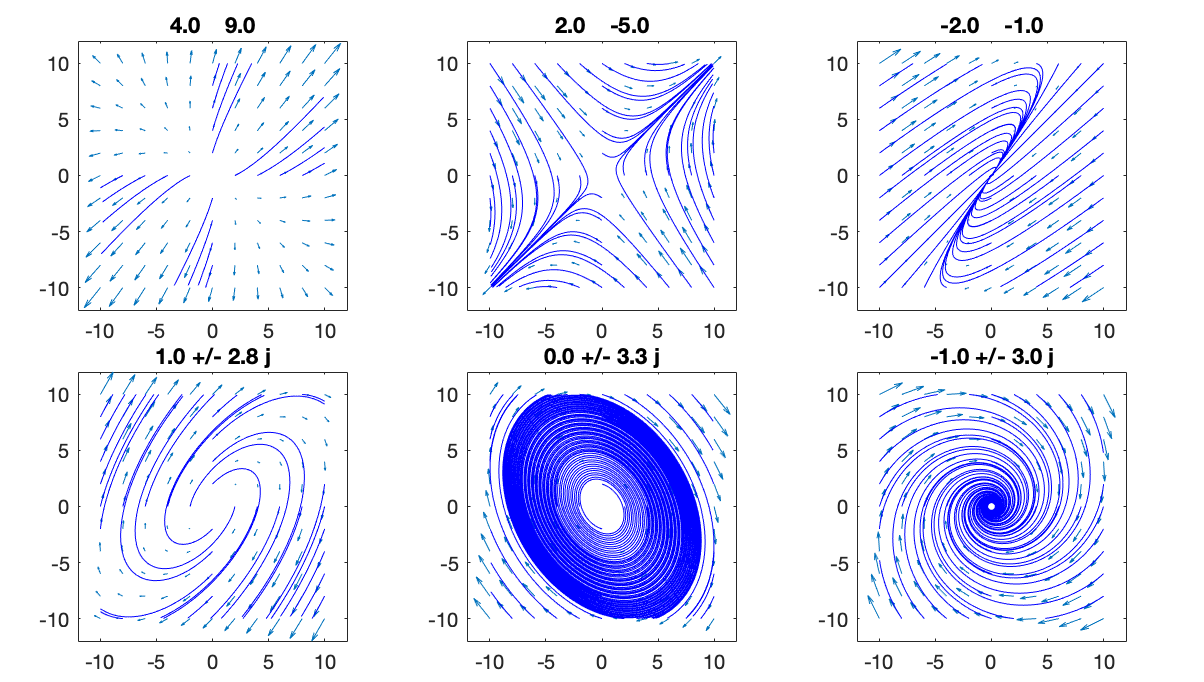
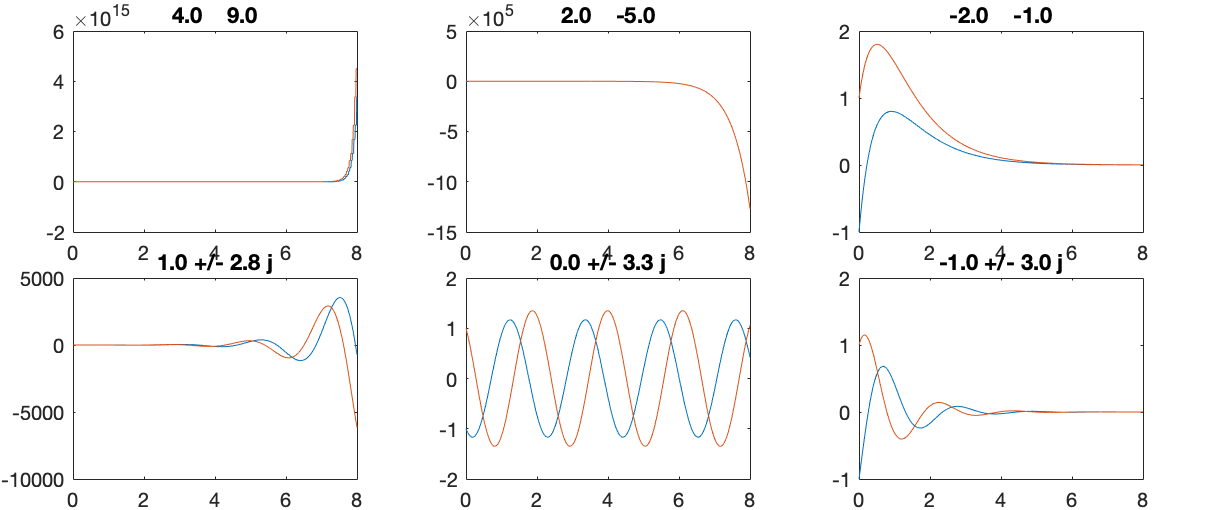
The behavior of the dynamic system described by a first order ODE
system can be visualized by the phase plane portrait, in
which the derivative
![${\bf y}'=[y'_1,\;y'_2]$](img420.svg) at each point
at each point
![${\bf y}=[y_1,\;y_2]^T$](img421.svg) is drawn as an arrow, as shown in the
examples below:
is drawn as an arrow, as shown in the
examples below:
![$\displaystyle \left[\begin{array}{rr}6&2\\ 3&7\end{array}\right],\;\;\;
\left[\...
...\end{array}\right],\;\;\;
\left[\begin{array}{rr}-1&3\\ -3&-1\end{array}\right]$](img422.svg) |
(164) |
 |
(165) |
The system is unstable if the real parts of any eigenvalue
is greater than zero (cases 1, 2, 4).
We next consider a set of coupled first order nonlinear ODE system
 |
(166) |
with initial condition
 .
This system can be expressed in vector form and Taylor expanded
in the neighborhood of an equilibrium point (satisfying
.
This system can be expressed in vector form and Taylor expanded
in the neighborhood of an equilibrium point (satisfying
 for all
for all  ):
):
 |
(167) |
where
 is the Jacobian matrix of
is the Jacobian matrix of  evaluated at
evaluated at
 :
:
![$\displaystyle {\bf J}_f(t,{\bf y}^*)=\left[\begin{array}{ccc}
\frac{\partial f_...
...dots &
\frac{\partial f_N}{\partial y_N} \end{array}\right]_{{\bf y}={\bf y}^*}$](img430.svg) |
(168) |
We see that the nonlinear ODE system can be locally linearized in the
neighborhood of the equilibrium point  to become a linear
ODE system in the form of
to become a linear
ODE system in the form of
 . The
behavior of the solution in the neighborhood of the equilibrium point
depends on the eigenvalues of
. The
behavior of the solution in the neighborhood of the equilibrium point
depends on the eigenvalues of
 .
.
Example:
The motion of a simple pendulum can be described by the following
second-order ODE:
 |
(169) |
where  is the damping coefficient,
is the damping coefficient,  is the length of the
support rod, and
is the length of the
support rod, and  is gravitational acceleration.
This nonlinear ODE can be linearized if we can assume the angle
is gravitational acceleration.
This nonlinear ODE can be linearized if we can assume the angle
 is small, and consider the Maclaurin expansion of
is small, and consider the Maclaurin expansion of
 :
:
 |
(170) |
and we get a LCCODE
 |
(171) |
This second order ODE can be converted into two first-order ODEs
 |
(172) |
or in vector form:
![$\displaystyle {\bf y}'=\left[\begin{array}{c}\theta\\ \omega\end{array}\right]'...
...ft[\begin{array}{l}f_1=\omega\\ f_2=-c\,\omega-g\sin\theta/L \end{array}\right]$](img441.svg) |
(173) |
The equilibrium point satisfies
From the second equation we get
 , i.e., there are
two equilibrium points
, i.e., there are
two equilibrium points
 and
and
 . In the neighborhood of the
equilibrium point
. In the neighborhood of the
equilibrium point  satisfying
satisfying
 , we have
, we have
![$\displaystyle {\bf y}' \approx {\bf J}_f{\bf y}=\left[\begin{array}{cc}
\frac{\...
...right]
=\left[\begin{array}{cc} 0 & 1 \\ -g\cos\theta/L & -c
\end{array}\right]$](img450.svg) |
(175) |
Consider the two cases:
The phase planes of the pendulum problem corresponding to
 and
and  are shown below. We see that the equiliburim
point
are shown below. We see that the equiliburim
point
 is stable while the equiliburim
point
is stable while the equiliburim
point
 is unstable (saddle point).
is unstable (saddle point).
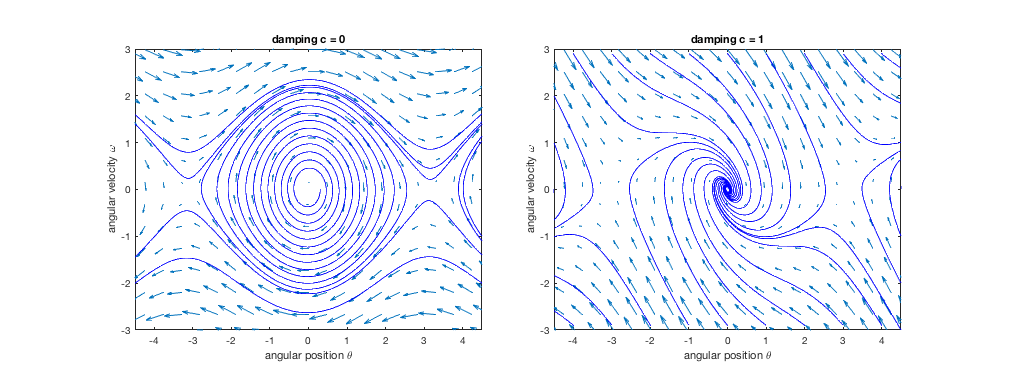
We next consider the complete solution of a second order LCCODE
in the following canonical form:
 |
(178) |
Same as in the first order case, the complete solution of this
second order LCCODE is composed of the
homogeneous solution  when
when  , and the
particular solution
, and the
particular solution  when
when  .
.
In the following, we will first consider various methods
for solving first-order ODEs, and then extend such methods
to solving first order ODE systems containing multiple ODEs
 , and
higher order ODEs
, and
higher order ODEs
 .
.

 or
or![$\displaystyle \;\;\;\;\;\;\;\;
\left[\begin{array}{l} y_1'(t)\\ y_2'(t)\end{arr...
...right]
=\left[\begin{array}{l}f_1(y_1,\;y_2)\\ f_2(y_1,\;y_2)\end{array}\right]$](img392.svg)
 . A phase plane plot
can be made to visualize certain properties such as the stability
of the solution. Specifically, let
. A phase plane plot
can be made to visualize certain properties such as the stability
of the solution. Specifically, let  and
and  span a 2-D
plane in which every point is associated with a vector with two
components
span a 2-D
plane in which every point is associated with a vector with two
components
![$\displaystyle {\bf f}=\left[\begin{array}{c}f_1\\ f_2\end{array}\right]
=\left[\begin{array}{c}y'_1\\ y'_2\end{array}\right]$](img395.svg)
 progresses. If the vector at a point
is zero
progresses. If the vector at a point
is zero
![$\displaystyle {\bf f}=\left[\begin{array}{l} f_1\\ f_2\end{array}\right]
=\left[\begin{array}{l} 0\\ 0\end{array}\right]={\bf0}$](img396.svg)
![$\displaystyle {\bf y}'=\left[\begin{array}{c}y_1\\ y_2\end{array}\right]'
=\lef...
... d\end{array}\right]
\left[\begin{array}{c}y_1\\ y_2\end{array}\right]={\bf Ay}$](img397.svg)
 is an equilibrium solution at
which
is an equilibrium solution at
which
 . As the solution of
this homogeneous system is in the following form:
. As the solution of
this homogeneous system is in the following form:

 :
:


![$\displaystyle \det
\left[\begin{array}{cc}\lambda-a & -b\\ -c & \lambda-d\end{array}\right]
=(\lambda-a)(\lambda-d)-bc$](img402.svg)


 and
and
 are the
trace and determinant of
are the
trace and determinant of  respectively, we can get the
eigenvalues of
respectively, we can get the
eigenvalues of 

 .
.

 (above the parabola), i.e.,
(above the parabola), i.e.,
 ,
then
,
then
 are two complex
conjugate roots,
are two complex
conjugate roots,

 (between the parabola and horizontal axis),
i.e.,
(between the parabola and horizontal axis),
i.e.,
 , then
, then
 are two real roots,
are two real roots,

 (below horizontal axis), i.e.,
(below horizontal axis), i.e.,
 ,
then
,
then
 have opposite signs,
unstable (saddle point);
have opposite signs,
unstable (saddle point);
 and
and  (the
top-left quadrant).
(the
top-left quadrant).
![${\bf y}'=[y'_1,\;y'_2]$](img420.svg)
![${\bf y}=[y_1,\;y_2]^T$](img421.svg)
![$\displaystyle \left[\begin{array}{rr}6&2\\ 3&7\end{array}\right],\;\;\;
\left[\...
...\end{array}\right],\;\;\;
\left[\begin{array}{rr}-1&3\\ -3&-1\end{array}\right]$](img422.svg)




 .
This system can be expressed in vector form and Taylor expanded
in the neighborhood of an equilibrium point (satisfying
.
This system can be expressed in vector form and Taylor expanded
in the neighborhood of an equilibrium point (satisfying
 for all
for all  ):
):

 is the Jacobian matrix of
is the Jacobian matrix of  evaluated at
evaluated at
 :
:
![$\displaystyle {\bf J}_f(t,{\bf y}^*)=\left[\begin{array}{ccc}
\frac{\partial f_...
...dots &
\frac{\partial f_N}{\partial y_N} \end{array}\right]_{{\bf y}={\bf y}^*}$](img430.svg)
 to become a linear
ODE system in the form of
to become a linear
ODE system in the form of
 . The
behavior of the solution in the neighborhood of the equilibrium point
depends on the eigenvalues of
. The
behavior of the solution in the neighborhood of the equilibrium point
depends on the eigenvalues of
 .
.

 is the damping coefficient,
is the damping coefficient,  is the length of the
support rod, and
is the length of the
support rod, and  is gravitational acceleration.
This nonlinear ODE can be linearized if we can assume the angle
is gravitational acceleration.
This nonlinear ODE can be linearized if we can assume the angle
 is small, and consider the Maclaurin expansion of
is small, and consider the Maclaurin expansion of
 :
:



![$\displaystyle {\bf y}'=\left[\begin{array}{c}\theta\\ \omega\end{array}\right]'...
...ft[\begin{array}{l}f_1=\omega\\ f_2=-c\,\omega-g\sin\theta/L \end{array}\right]$](img441.svg)






 , i.e., there are
two equilibrium points
, i.e., there are
two equilibrium points
 and
and
 . In the neighborhood of the
equilibrium point
. In the neighborhood of the
equilibrium point  satisfying
satisfying
 , we have
, we have
![$\displaystyle {\bf y}' \approx {\bf J}_f{\bf y}=\left[\begin{array}{cc}
\frac{\...
...right]
=\left[\begin{array}{cc} 0 & 1 \\ -g\cos\theta/L & -c
\end{array}\right]$](img450.svg)
 ,
,
 :
:

 , both eigenvalues
, both eigenvalues
 are purely
imaginary, the motion is a sinusoidal oscillation; if
are purely
imaginary, the motion is a sinusoidal oscillation; if  ,
,
 , the motion is an attenuated oscillation.
, the motion is an attenuated oscillation.
 ,
,
 :
:







 when
when  , and the
particular solution
, and the
particular solution  when
when  .
.

