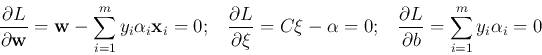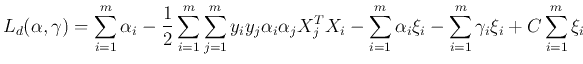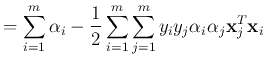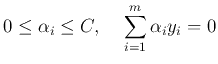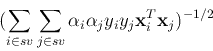Next: Kernel Mapping
Up: Soft Margin SVM
Previous: 2-Norm Soft Margin
The primal Lagrangian for 1-norm problem above is
with
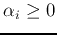 and
and
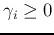 .
Substituting
.
Substituting
into the primal Lagrangian, we get the dual problem
Note that interestingly the objective function of the dual problem is
identical to that of the linearly separable problem discussed previously,
due to the nice cancellation based on
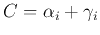 . Also, since
. Also, since
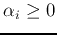 and
and
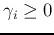 , we have
, we have
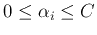 .
Solving this QP problem for
.
Solving this QP problem for 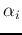 , we get the optimal decision plane
, we get the optimal decision plane
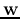 and
and 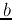 with the margin
with the margin
Ruye Wang
2016-08-24
![\begin{displaymath}L_p({\bf w},b,\xi,\alpha,\gamma)=\frac{1}{2}{\bf w}^T{\bf w}+...
...a_i[y_i({\bf w}^T{\bf x}+b)-1+\xi_i]-\sum_{i=1}^m\gamma_i\xi_i
\end{displaymath}](img132.png)
![\begin{displaymath}L_p({\bf w},b,\xi,\alpha,\gamma)=\frac{1}{2}{\bf w}^T{\bf w}+...
...a_i[y_i({\bf w}^T{\bf x}+b)-1+\xi_i]-\sum_{i=1}^m\gamma_i\xi_i
\end{displaymath}](img132.png)