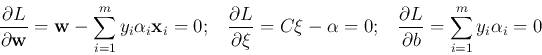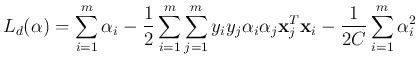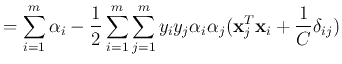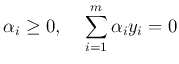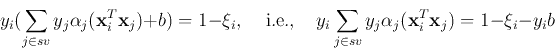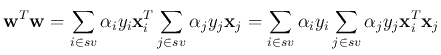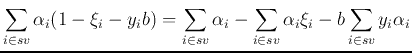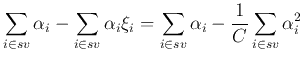Next: 1-Norm Soft Margin
Up: Soft Margin SVM
Previous: Soft Margin SVM
The primal Lagrangian for 2-norm problem above is
Substituting the following
into the primal Lagrangian, we get the dual problem
This QP program can be solved for 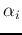 . All support vectors
. All support vectors 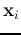 corresponding to
corresponding to 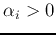 satisfy:
satisfy:
Substituting
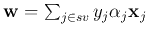 into this equation, we get
into this equation, we get
For the optimal weight 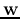 , we have
, we have
The last equation is due to
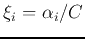 . The optimal margin is
. The optimal margin is



Next: 1-Norm Soft Margin
Up: Soft Margin SVM
Previous: Soft Margin SVM
Ruye Wang
2016-08-24
![\begin{displaymath}L_p({\bf w},b,\xi,\alpha)=\frac{1}{2}{\bf w}^T{\bf w}+\frac{C...
...i_i^2
-\sum_{i=1}^m \alpha_i[y_i({\bf w}^T{\bf x}+b)-1+\xi_i]
\end{displaymath}](img121.png)
![\begin{displaymath}L_p({\bf w},b,\xi,\alpha)=\frac{1}{2}{\bf w}^T{\bf w}+\frac{C...
...i_i^2
-\sum_{i=1}^m \alpha_i[y_i({\bf w}^T{\bf x}+b)-1+\xi_i]
\end{displaymath}](img121.png)