


Next: About this document ...
Up: Support Vector Machines (SVM)
Previous: 1-Norm Soft Margin
The algorithm above converges only for linearly separable data. If the
data set is not linearly separable, we can map the samples 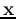 into a feature space of higher dimensions:
into a feature space of higher dimensions:
in which the classes can be linearly separated. The decision function in
the new space becomes:
where
and 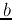 are the parameters of the decision plane in the new space.
As the vectors
are the parameters of the decision plane in the new space.
As the vectors 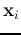 appear only in inner products in both the decision
function and the learning law, the mapping function
appear only in inner products in both the decision
function and the learning law, the mapping function 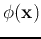 does not
need to be explicitly specified. Instead, all we need is the inner
product of the vectors in the new space. The function
does not
need to be explicitly specified. Instead, all we need is the inner
product of the vectors in the new space. The function 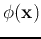 is a
kernel-induced implicit mapping.
is a
kernel-induced implicit mapping.
Definition: A kernel is a function that takes two vectors 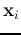 and
and 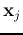 as arguments and returns the value of the inner product of
their images
as arguments and returns the value of the inner product of
their images
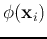 and
and
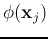 :
:
As only the inner product of the two vectors in the new space is returned,
the dimensionality of the new space is not important.
The learning algorithm in the kernel space can be obtained by replacing
all inner products in the learning algorithm in the original space with
the kernels:
The parameter 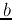 can be found from any support vectors
can be found from any support vectors 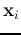 :
:
Example 0: linear kernel
Assume
![${\bf x}=[x_1,\cdots,x_n]^T$](img149.png) ,
,
![${\bf z}=[z_1,\cdots,z_n]^T$](img150.png) ,
,
Example 1: polynomial kernels
Assume
![${\bf x}=[x_1, x_2]^T$](img16.png) ,
,
![${\bf z}=[z_1,z_2]^T$](img152.png) ,
,
This is a mapping from a 2-D space to a 3-D space. The order can be changed
from 2 to general d.
Example 2:
Example 3:



Next: About this document ...
Up: Support Vector Machines (SVM)
Previous: 1-Norm Soft Margin
Ruye Wang
2016-08-24
![]() into a feature space of higher dimensions:
into a feature space of higher dimensions:
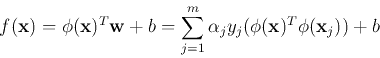
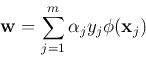
![]() and
and ![]() as arguments and returns the value of the inner product of
their images
as arguments and returns the value of the inner product of
their images
![]() and
and
![]() :
:
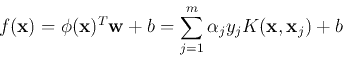
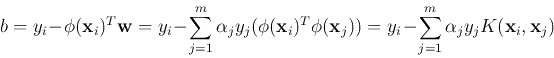
![]() ,
,
![]() ,
,
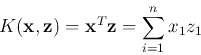
![]() ,
,
![]() ,
,