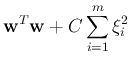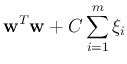Next: 2-Norm Soft Margin
Up: Support Vector Machines (SVM)
Previous: Support Vector Machine
When the two classes are not linearly separable, the condition for the
optimal hyper-plane can be relaxed by including an extra term:
For minimum error, 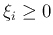 should be minimized as well as
should be minimized as well as 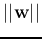 ,
and the objective function becomes:
,
and the objective function becomes:
Here 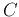 is a regularization parameter that controls the trade-off between
maximizing the margin and minimizing the training error. Small C tends to
emphasize the margin while ignoring the outliers in the training data, while
large C may tend to overfit the training data.
is a regularization parameter that controls the trade-off between
maximizing the margin and minimizing the training error. Small C tends to
emphasize the margin while ignoring the outliers in the training data, while
large C may tend to overfit the training data.
When 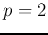 , it is called 2-norm soft margin problem:
, it is called 2-norm soft margin problem:
Note that the condition 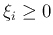 is dropped, as if
is dropped, as if 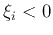 , we can
set it to zero and the objective function is further reduced.)
Alternatively, if we let
, we can
set it to zero and the objective function is further reduced.)
Alternatively, if we let 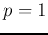 , the problem can be formulated as
, the problem can be formulated as
This is called 1-norm soft margin problem. The algorithm based on 1-norm
setup, when compared to 2-norm algorithm, is less sensitive to outliers in
training data. When the data is noisy, 1-norm method should be used to
ignore the outliers.
Subsections



Next: 2-Norm Soft Margin
Up: Support Vector Machines (SVM)
Previous: Support Vector Machine
Ruye Wang
2016-08-24
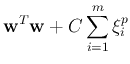
![]() , it is called 2-norm soft margin problem:
, it is called 2-norm soft margin problem: