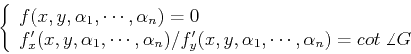The
gradient direction ![]() of an edge pixel
can be used to reduce the computation in the
parameter space. First recall that the tangent direction or the derivative
of an edge pixel
can be used to reduce the computation in the
parameter space. First recall that the tangent direction or the derivative
![]() of an implicit function
of an implicit function ![]() can be found as:
can be found as:
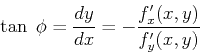
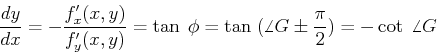
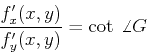
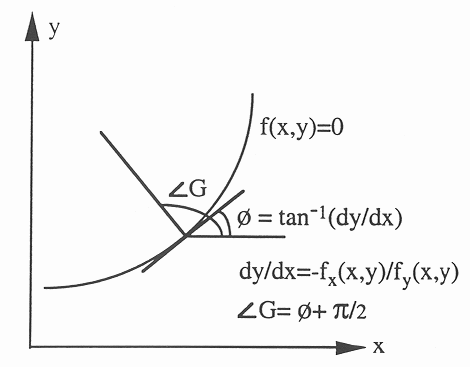
Now the gradient direction ![]() can be used to establish a second
equation, in addition to the original equation describing the shape, and
thereby reducing the dimensions of the hyper-surface in the parameter space
that needs to be incremented by 1.
can be used to establish a second
equation, in addition to the original equation describing the shape, and
thereby reducing the dimensions of the hyper-surface in the parameter space
that needs to be incremented by 1.