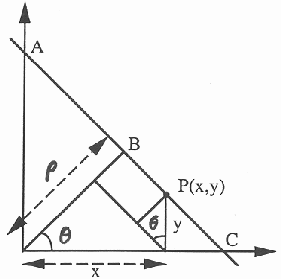
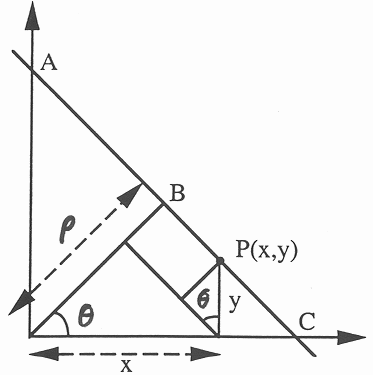
A straight line in 2D space described by this parametric equation:
To find the Hough transform of a certain point ![]() in the image space,
we solve the equation above for
in the image space,
we solve the equation above for ![]() and get
and get
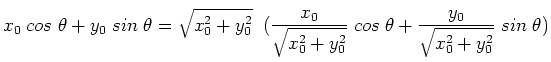 |
|||
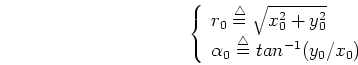
We see from the equation above that any point ![]() in the image
space is transformed into a sinusoidal curve in the parameter space.
On the other hand, a point
in the image
space is transformed into a sinusoidal curve in the parameter space.
On the other hand, a point
![]() on this sinusoidal curve
represents a straight line passing through the point
on this sinusoidal curve
represents a straight line passing through the point ![]() in
the image space, as shown in the figures below, where
in
the image space, as shown in the figures below, where ![]() , i.e.,
, i.e.,
![]() ,
,
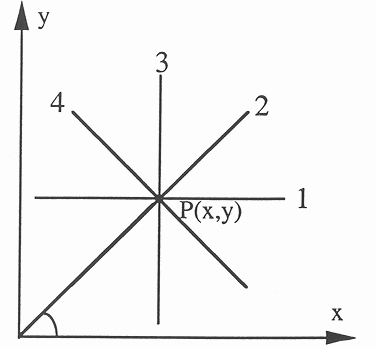
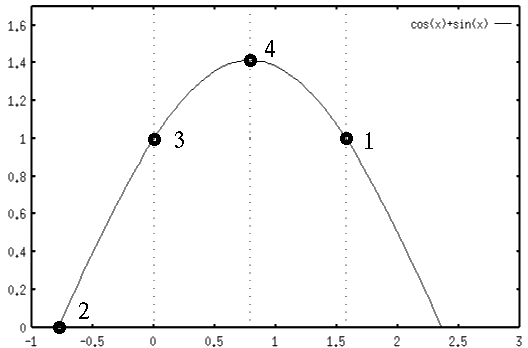
![]() . Note that the four
particular directions labeled as 2, 3, 4 and 1 in the image (left) correspond
respectively to the points in the Hough space (right):
. Note that the four
particular directions labeled as 2, 3, 4 and 1 in the image (left) correspond
respectively to the points in the Hough space (right):

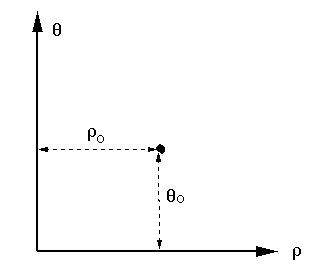
Any given point
![]() in the parameter space can be inverse
transformed to the spatial domain to represent a straight line specified by
the equation
in the parameter space can be inverse
transformed to the spatial domain to represent a straight line specified by
the equation
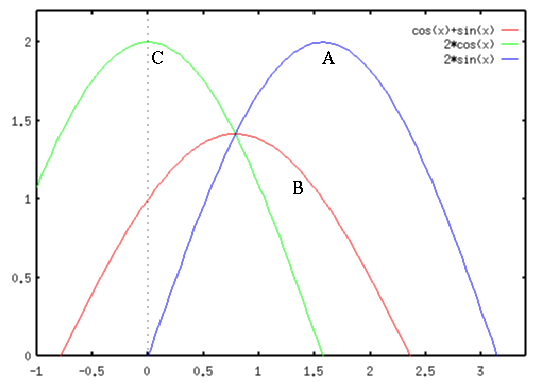
The figures below show an example of three image points ![]() ,
, ![]() , and
, and
![]() all on a straight line. These points are mapped to the parameter space as
three sinusoidal curves in blue, red and green, respectively. The fact that these
points are on a straight line guarantees that the corresponding curves intersect at
a point (
all on a straight line. These points are mapped to the parameter space as
three sinusoidal curves in blue, red and green, respectively. The fact that these
points are on a straight line guarantees that the corresponding curves intersect at
a point (
![]() and
and
![]() ) representing the straight line
) representing the straight line
The ddetection of all straight lines in the image can be carried out by the following steps:
for all ![]() {
{
This algorithm can be improved by making use of the gradient direction
![]() , which, in this particular case, is the same as the angle
, which, in this particular case, is the same as the angle ![]() .
Now for any point
.
Now for any point
![]() , we only need to increment the elements on
a small segment of the sinusoidal curve. The third step in the above algorithm
can be modified as:
, we only need to increment the elements on
a small segment of the sinusoidal curve. The third step in the above algorithm
can be modified as:
for all ![]() satisfying
satisfying
![]()
{
where ![]() defines a small range in
defines a small range in ![]() to allow some room for
error in
to allow some room for
error in ![]() .
.
Check out this online demo.