


Next: Compass Gradient Operations
Up: gradient
Previous: The Gradient Operator
For discrete digital images, the derivative in gradient operation
becomes the difference
Two steps for finding discrete gradient of a digital image:
- Find the difference:
in the two directions:
- Find the magnitude and direction of the gradient vector:
The differences in two directions 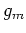 and
and 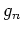 can be obtained by
convolution with the following kernels:
can be obtained by
convolution with the following kernels:
- Roberts
or
- Sobel (3x3)
- Prewitt (3x3)
- Prewitt (4x4)
Note Sobel and Prewitt operators first find the averages of one direction
and then find the difference of these averages in the another direction.



Next: Compass Gradient Operations
Up: gradient
Previous: The Gradient Operator
Ruye Wang
2016-10-18
![\begin{displaymath}\angle g[m,n]=\tan^{-1} \left(\frac{g_n[m,n]}{g_m[m,n]}\right) \end{displaymath}](img47.png)
![]() and
and ![]() can be obtained by
convolution with the following kernels:
can be obtained by
convolution with the following kernels:
![\begin{displaymath}\left[ \begin{array}{rr} -1 & 1 0 & 0 \end{array} \right],...
...
\left[ \begin{array}{rr} -1 & 0 1 & 0 \end{array} \right]
\end{displaymath}](img50.png)
![\begin{displaymath}\left[ \begin{array}{rr} 0 & 1 -1 & 0 \end{array} \right],...
...
\left[ \begin{array}{rr} 1 & 0 0 & -1 \end{array} \right]
\end{displaymath}](img51.png)
![\begin{displaymath}\left[ \begin{array}{rrr} -1 & 0 & 1 -2 & 0 & 2 -1 & 0 ...
...} -1 & -2 & -1 0 & 0 & 0 1 & 2 & 1
\end{array} \right]
\end{displaymath}](img52.png)
![\begin{displaymath}\left[ \begin{array}{rrr} -1 & 0 & 1 -1 & 0 & 1 -1 & 0 ...
...} -1 & -1 & -1 0 & 0 & 0 1 & 1 & 1
\end{array} \right]
\end{displaymath}](img53.png)
![\begin{displaymath}\left[ \begin{array}{rrrr} -3 & -1 & 1 & 3 -3 & -1 & 1 & 3...
...1 & -1 \\
1 & 1 & 1 & 1 3 & 3 & 3 & 3 \end{array} \right]
\end{displaymath}](img54.png)