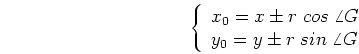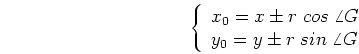Next: Detection of Ellipses
Up: hough
Previous: Make Use of
A circle in the image can be described by
where 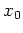 ,
, 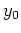 , and
, and 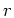 are three parameters which span a 3D Hough space.
Any point
are three parameters which span a 3D Hough space.
Any point 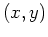 in the image corresponds to a cone shaped surface in the 3D
parameter space. To use
in the image corresponds to a cone shaped surface in the 3D
parameter space. To use 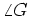 , consider the derivative
, consider the derivative
Now we only need to increment those elements in the parameter space that
satisfy both of the following equations
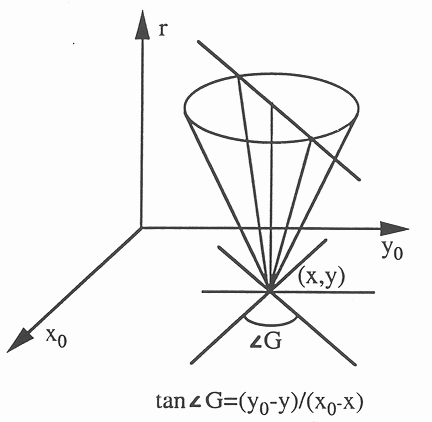
Geometrically these two simultaneous equations represent the intersection of
a cone specified by the first equation and a plane specified by the second
equation which passes through the axis of the cone, as shown in the figure below.
Solving these equations for 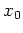 and
and 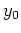 , we get
, we get
and the algorithm for detecting circles:
- For any pixel satisfying
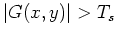 , increment all elements
satisfying the two simultaneous equations above;
, increment all elements
satisfying the two simultaneous equations above;
for all 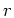
{
}
- In the parameter space, any element
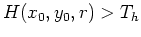 represents a circle with radius
represents a circle with radius 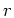 located at
located at 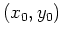 in the image.
in the image.



Next: Detection of Ellipses
Up: hough
Previous: Make Use of
Ruye Wang
2009-11-17
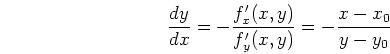
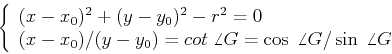

![]() and
and ![]() , we get
, we get