The Twin-T notch (band-stop) filter

The twin-T filter

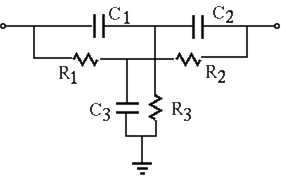
The twin-T network is composed of two T-networks:

• The RCR network is formed by two resistors $R_1=R_2=R$ and one capacitor $C_3=2C$.

• The CRC network is formed by two capacitors $C_1=C_2=C$ and one resistor $R_3=R/2$.

By simple observation we see that when the output is an open-circuit with $Z_L=\infty$, a sinusoidal signal can pass the twin-T when the frequency is either very low $\omega\approx 0$ or very high $\omega\rightarrow\infty$. More specifically, the frequency response function of the twin-T network can be found to be (see here):

$$H(j\omega) = \frac{v_{out}}{v_{in}} =\frac{(j\omega)^2+\omega_n^2}{(j\omega)^2+4\omega_nj\omega+\omega_n^2}$$

$$= \frac{(j\omega)^2+\omega_n^2}{(j\omega)^2+j\omega\omega_n/Q+\omega_n^2} =\frac{\omega^2-\omega_n^2}{\omega^2-j\omega\Delta\omega-\omega_n^2}$$ (36)

where

  $$\omega_n=\frac{1}{RC}=\frac{1}{\tau},\;\;\;Q=\frac{1}{4},\;\;\;\; \Delta\omega=\frac{\omega_n}{Q}=4\omega_n$$ (37)

This twin-T network is a band-stop filter (notch filter) which attenuates the frequency $\omega_n=1/\tau$ to zero:

  $$\vert H(j\omega)\vert=\left\{\begin{array}{ll} H(0)=\omega_n^2/... ...}H(j\omega)=\omega^2/\omega^2=1 & \omega\rightarrow \infty \end{array}\right.$$ (38)

This result can also be reached by noticing the following

  $$H'(j\omega)\big\vert _{\omega=1/\tau}=\frac{1}{1+j2},\;\;\;\;\;\;\; H''(j\omega)\big\vert _{\omega=1/\tau}=\frac{1}{1-j2}$$ (39)

As they are equal in magnitude but opposite in phase, their outputs cancel each other to produce zero output.

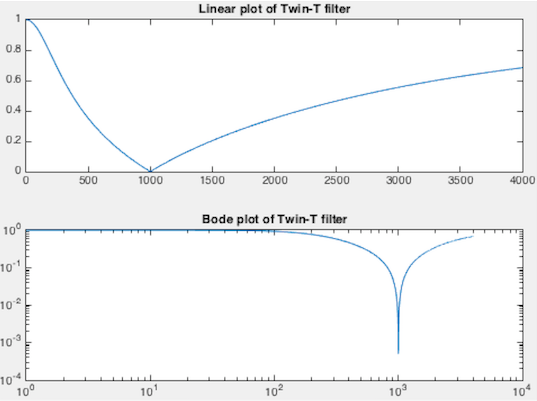
When this notch filter is used in a negative feedback loop of an amplifier, it becomes an oscillator.

The active twin-T filter

The bandwidth $\Delta\omega=\omega_n/Q=4\omega_n$ may not be narrow enough for most applications due to the small quality factor $Q=1/4$. To overcome this problem, an active filter containing two op-amp followers (with unity gain $A=1$) can be used to introduce a positive feedback loop as shown below:

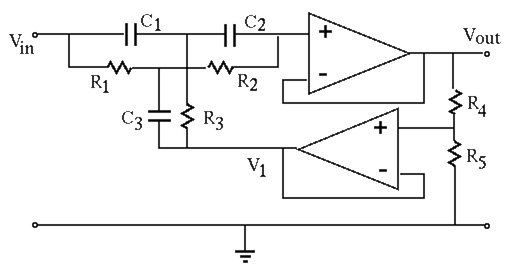
Now the common terminal of the twin-T filter is no longer grounded, instead it is connected a potentiometer, a voltage divider composed of $R_4$ and $R_5$, to form a feedback loop by which a fraction of the output $V_{out}$ is fed back:

  $$V_1=\frac{R_5}{R_4+R_5}\;V_{out}=\alpha v_{out}$$ (40)

where $\alpha=R_5/(R_4+R_5)$, i.e., $1-\alpha=R_4/(R_4+R_5)$.

The input and output of the twin-T network are respectively $V_{in}-V_1$ and $V_{out}-V_1$, and they are now related by the frequency response function $H(j\omega)$ of the twin-T network:

  $$V_{out}-V_1=H(j\omega)(V_{in}-V_1)$$ (41)

Rearranging and substituting $V_1=V_{out}\;R_5/(R_4+R_5)$, we get

$$H(j\omega)V_{in} = V_{out}+(H(j\omega)-1) V_1 =V_{out}+(H(j\omega)-1)\frac{R_5}{R_4+R_5}V_{out}$$

$$= \left(1+(H(j\omega)-1)\;\frac{R_5}{R_4+R_5}\right)\,V_{out} =\frac{R_4+H(j\omega)R_5}{R_4+R_5}\;V_{out}$$ (42)

Now the frequency response function of this active filter with feedback can be found to be

  $$H_{active}(j\omega)=\frac{V_{out}}{V_{in}} =\frac{H(j\omega)(R_4+R_5)}{R_4+H(j\omega)R_5}$$ (43)

Substituting $H(j\omega)=((j\omega)^2+\omega_n^2)/((j\omega)^2+4\omega_n j\omega +\omega_n^2)$ we get

$$H_{active}(j\omega) = \frac{(\omega_n^2-\omega^2)(R_4+R_5)} {R_4(\omega_n^2-\omega^2+4\omega_n j\omega)+(\omega_n^2-\omega^2)R_5}$$

$$= \frac{(\omega_n^2-\omega^2)(R_4+R_5)} {4\omega_nR_4 j\omega+(\omega_n^2-\omega^2)(R_4+R_5)}$$

$$= \frac{\omega_n^2-\omega^2}{j\omega 4\omega_n R_4/(R_4+R_5)+\omega_n^2-\omega^2}$$

$$= \frac{\omega_n^2-\omega^2}{\omega_n^2-\omega^2+\omega_n/Q_{active... ... =\frac{\omega^2-\omega_n^2}{\omega^2-\Delta\omega_{active} j\omega-\omega^2_n}$$ (44)

where

  $$Q_{active}=\frac{R_4+R_5}{4R_4},\;\;\;\;\;\; \Delta\omega_{active}=\frac{\omega_n}{Q}_{active}$$ (45)

are respectively the quality factor and the bandwidth of the active filter with feedback. By changing $R_4$ and $R_5$, the bandwidth $\Delta\omega_{active}$ can be adjusted. In particular,

• when $R_5=0$, $V_1=0$ (no feedback), $Q_{active}=1/4=Q$, $\Delta\omega=\omega_n/Q=4\omega_n$;
• when $R_4=0$, $V_1=V_{out}$ (one hundred percent feedback), $Q_{active}=\infty$, $\Delta\omega_{active}=\omega_n/Q_{active}=0$.

The bridged T filter

If in the RCR T-network the vertical capacitor branch is dropped, i.e., $C=0$, the twin-T network becomes a bridged T network. Now we have $Z'_3=2R$, while the CRC T-network is still the same with $Z''_3=2(1+j\omega RC)/R(j\omega C)^2$, we get:

  $$Z_3=Z'_3\vert\vert Z''_3=\frac{Z'_3 Z''_3}{Z'_3+Z''_3} =\frac{2R(1+j\omega RC)}{1+j\omega RC+(j\omega RC)^2}$$ (46)

The frequency response function of this bridged T network (a voltage divider) is:

$$H(j\omega) = \frac{Z_2}{Z_2+Z_3}=\frac{R+1/j\omega C}{R+1/j\omega C+2R(1+j\omega RC)/(1+j\omega RC+(j\omega RC)^2)}$$

$$= \frac{1/C}{1/j\omega C+2R/(1+j\omega RC+(j\omega RC)^2)} =\frac{1}{1+2j\omega RC/(1+j\omega RC+(j\omega RC)^2)}$$

$$= \frac{1+j\omega RC+(j\omega RC)^2}{1+3j\omega RC+(j\omega RC)^2} =\frac{(j\omega)^2+j\omega /RC+1/(RC)^2}{(j\omega)^2+3j\omega /RC+1/(RC)^2}$$ (47)

We let $\omega_n=1/RC$, and express both the numerator and the denominator in the canonical form as

  $$H(j\omega)=\frac{(j\omega)^2+\omega_n j\omega +\omega_n^2}{(j\ome... ...2-\omega^2+\Delta\omega_n j\omega }{\omega_n^2-\omega^2+\Delta\omega_dj\omega}$$ (48)

where

  $$\Delta\omega_n=\omega_n,\;\;\;\;\;\;\;\Delta\omega_d=3\omega_n$$ (49)

are the bandwidth of the 2nd-order systems of the numerator and the denominator, respectively.

• If $\omega=0$, $H(j\omega)=H(0)=1$
• If $\omega\rightarrow\infty$, $H(j\omega)=1$
• If $\omega=\omega_n=1/RC$, $H(j\omega_n)=1/3$

We see that this is a band-stop filter.