The Sallen-Key filters

A Sallen-Key filter with the general configuration shown below is a second-order active filter that can be used to implement any of the low-pass, high-pass, and band-pass filtering.

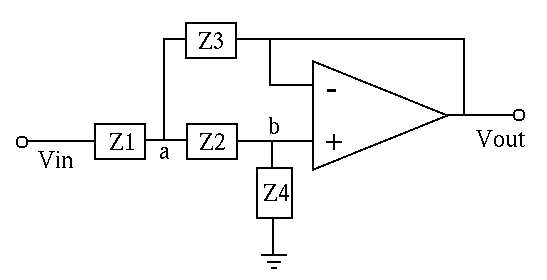
To find the frequency response function of the filter, we find the output voltage as a function of the input voltage both represented in phasor form, and apply the virtual ground assumption $V_b\approx V_-=V_{out}$ and the KCL to nodes a and b:

  $$\frac{V_a-V_{in}}{Z_1}+\frac{V_a-V_{out}}{Z_3}+\frac{V_a-V_{out}}... ...frac{V_a-V_{in}}{Z_1}+(V_a-V_{out})\left(\frac{1}{Z_3}+\frac{1}{Z_2}\right)=0$$ (13)

and

  $$\frac{V_{out}-V_a}{Z_2}+\frac{V_{out}}{Z_4}=0,$$ (14)

Solving the second equation for $V_a$, we get

  $$V_a=V_{out}\frac{Z_2+Z_4}{Z_4}$$ (15)

We then substitut this into the first equation to get

  $$V_{out}\;\left(\frac{Z_2+Z_4}{Z_1Z_4}+\frac{Z_2}{Z_3Z_4}+\frac{Z_2}{Z_2Z_4} \right) =\frac{V_{in}}{Z_1}$$ (16)

Now the frequency response function can be found as the ratio of $V_{out}$ and $V_{in}$:

$$H = \frac{V_{out}}{V_{in}}=\frac{Z_3Z_4}{Z_1Z_2+Z_1Z_3+Z_2Z_3+Z_3Z_4}$$ (17)

• Second order low-pass filter

  If we let $Z_1=R_1$, $Z_2=R_2$, $Z_3=1/j\omega C_1$, $Z_4=1/j\omega C_2$, the FRF becomes (see here):

    $$H(j\omega)=\frac{\omega_n^2}{(j\omega)^2+\Delta\omega\;j\omega+\omega_n^2}$$ (18)

  where

    $$\omega_n=\frac{1}{\sqrt{R_1R_2C_1C_2}},\;\;\;\;\;\;\; \Delta\ome... ...)C_1}=\frac{1}{R_pC_1},\;\;\;\; R_p=R_1\vert\vert R_2=\frac{R_1R_2}{R_1+R_2}$$ (19)
  and
    $$Q=\frac{\omega_n}{\Delta\omega}=\frac{\sqrt{R_1R_2C_1C_2}}{(R_1+R... ...2}, \;\;\;\;\; \zeta=\frac{1}{2Q}=\frac{(R_1+R_2)C_2}{2\sqrt{R_1R_2C_1C_2}}$$ (20)
  To satisfy the two parameters $\omega_n$ and $\zeta$ or $Q=1/2\zeta$ of a desired filter, we can arbitrarily set any two of the four variables $R_1$, $R_2$, $C_1$, and $C_2$, and then solve for the other two. For example, for convenience, if we let $R_1=R_2=1$, we get
    $$\omega_n=\frac{1}{\sqrt{C_1C_2}},\;\;\;\;\;\Delta\omega=\frac{1}{C_1}$$ (21)

• Second order high-pass filter

  If we let $Z_1=1/j\omega C_1$, $Z_2=1/j\omega C_2$, $Z_3=R_1$, $Z_4=R_2$, the FRF becomes (see here):

    $$H(j\omega)=\frac{(j\omega)^2}{(j\omega)^2+\Delta\omega\;j\omega+\omega_n^2}$$ (22)
  where
    $$\omega_n=\frac{1}{\sqrt{R_1R_2C_1C_2}},\;\;\;\;\;\;\; \Delta\omega=\frac{1}{C_sR_2},\;\;\;\;\; C_s=\frac{C_1C_2}{C_1+C_2}$$ (23)
  and
    $$Q=\frac{\sqrt{R_1R_2C_1C_2}}{(C_1+C_2)R_1},\;\;\;\;\;\; \zeta=\frac{1}{2Q}=\frac{(C_1+C_2)R_1}{2\sqrt{R_1R_2C_1C_2}}$$ (24)

• Band-pass filter

  

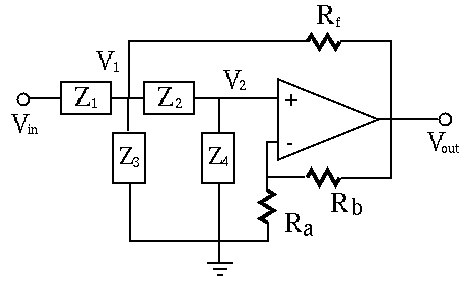
  By voltage divider and virtual ground, we get

    $$V_2=\frac{R_a}{R_a+R_b}V_{out}=kV_{out},\;\;\;\;\;\;\;\left(k=\frac{R_a}{R_a+R_b}\right)$$ (25)
  Apply KCL to node $V_2$ to get:
    $$\frac{V_1-V_2}{Z_2}=\frac{V_2}{Z_4},\;\;\;\;\;\;\;\mbox{i.e.}\;\;\;\;\; V_1=V_2\left(1+\frac{Z_2}{Z_4}\right)$$ (26)
  Apply KCL to node $V_1$ to get:
    $$\frac{V_{in}-V_1}{Z_1}+\frac{V_{out}-V_1}{R_f}+\frac{V_2-V_1}{Z_2} =\frac{V_1}{Z_3}$$ (27)
  Rearranging the terms, and substituting $V_2(1+Z_2/Z_4)$ for $V_1$ we get
  

  $$\frac{V_{in}}{Z_1}+\frac{V_{out}}{R_f}+\frac{V_2}{Z_2} =V_1\left(\frac{1}{Z_1}+\frac{1}{R_f}+\frac{1}{Z_2}+\frac{1}{Z_3}\right)$$

  $$= V_2\left(1+\frac{Z_2}{Z_4}\right)\left(\frac{1}{Z_1} +\frac{1}{R_f}+\frac{1}{Z_2}+\frac{1}{Z_3}\right)$$ (28)

  Further rearrange the terms and replace $V_2$ by $kV_{out}$ to get
    $$\frac{V_{in}}{Z_1}+\frac{V_{out}}{R_f} =kV_{out}\left[\left(1+\f... ...{Z_1}+\frac{1}{R_f} +\frac{1}{Z_2}+\frac{1}{Z_3}\right)-\frac{1}{Z_2}\right]$$ (29)
  Further rearrange the terms
  

  $$\frac{V_{in}}{Z_1} = kV_{out}\left[\left(1+\frac{Z_2}{Z_4}\right) \left(\frac{1}{Z_1} ... ..._f}+\frac{1}{Z_2}+\frac{1}{Z_3}\right)-\frac{1}{Z_2}\right]-\frac{V_{out}}{R_f}$$

  $$= V_{out}\left\{k\left[\left(1+\frac{Z_2}{Z_4}\right)\left(\frac{1}... ...}+\frac{1}{Z_2}+\frac{1}{Z_3}\right)-\frac{1}{Z_2}\right]-\frac{1}{R_f}\right\}$$ (30)

  Finally we get the frequency response function:
  

  $$H=\frac{V_{out}}{V_{in}} = \frac{1}{Z_1\left\{k\left[\left(1+\frac{Z_2}{Z_4}\right)\left(\fr... ...+\frac{1}{Z_2}+\frac{1}{Z_3}\right)-\frac{1}{Z_2}\right]-\frac{1}{R_f}\right\}}$$

  $$= \frac{1/k}{Z_1\left[\left(1+\frac{Z_2}{Z_4}\right)\left(\frac{1}{... ...{R_f}+\frac{1}{Z_2}+\frac{1}{Z_3}\right)-\frac{1}{Z_2}\right]-\frac{Z_1}{kR_f}}$$

  $$= \frac{1/k}{1+\frac{Z_1}{R_f}+\frac{Z_1}{Z_3}+\frac{Z_2}{Z_4}+\frac{Z_1Z_2}{Z_4R_f}+\frac{Z_1}{Z_4}+\frac{Z_1Z_2}{Z_3Z_4}-\frac{Z_1}{kR_f}}$$ (31)

  Now if we let
    $$Z_1=R_1,\;\;\;\;\;Z_4=R_2,\;\;\;\;Z_2=\frac{1}{j\omega C_2}, \;\;\;\;Z_3=\frac{1}{j\omega C_1}$$ (32)
  the frequency response function becomes
  

  $$H = \frac{\left(1+\frac{R_b}{R_a}\right)\frac{1}{R_1C_1}j\omega}{(j\o... ...1}{R_1C_1}-\frac{R_b}{R_aR_fC_1}\right)j\omega+\frac{R_1+R_f}{R_fR_1R_2C_1C_2}}$$

  $$= \frac{Aj\omega}{(j\omega)^2+\Delta\omega j\omega+\omega_n^2}, \;\;\;\;\;\;\;\;\; A=(1+R_b/R_a)/R_1C_1$$ (33)

  This is a band-pass filter with the peak frequency equal to the natural frequency:
    $$\omega_n=\sqrt{\frac{R_1+R_f}{R_fR_1R_2C_1C_2}}$$ (34)
  the bandwidth
    $$\Delta\omega=\frac{1}{R_2C_1}+\frac{1}{R_2C_2}+\frac{1}{R_1C_1}-\frac{R_b}{R_aR_fC_1}$$ (35)
  The gain of the filter is controlled by $1+R_b/R_a$.

Example:

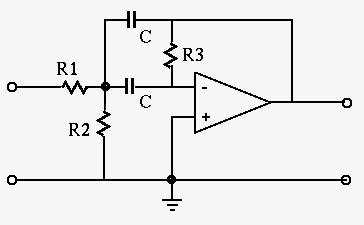
where $C=10^{-5}\,\mu F$, $R_1=8\,k\Omega,\; R_2=0.16\,k\Omega,\;R_3=16\,k\Omega$.