Next: The Sallen-Key filters Up: Chapter 6: Active Filter Previous: Chapter 6: Active Filter
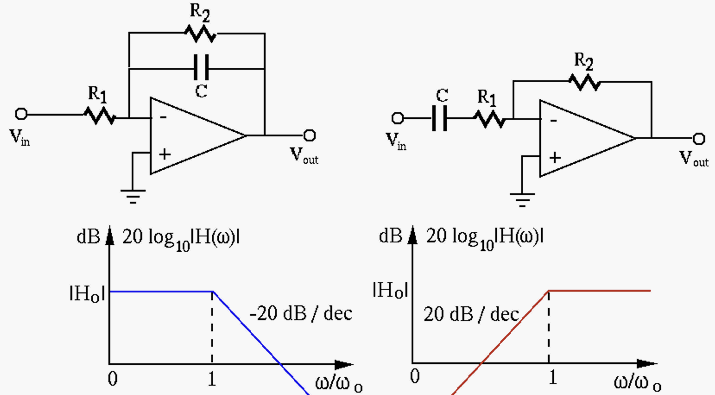
Consider the two active filters shown below and determine what kind of filters they are.
Qualitatively, we see that this is a low-pass filter as
 (1)
(1)
 when
when
 .
.
Specifically,
 |
 |
 |
|
 |
 |
(2) |
 is the DC gain when
is the DC gain when  , and
, and
 is cut-off or corner frequency, at which
is cut-off or corner frequency, at which
 . Intuitively, when frequency is high,
. Intuitively, when frequency is high,
 is small and the negative feedback becomes strong,
and the output is low. For example, when
is small and the negative feedback becomes strong,
and the output is low. For example, when
 ,
,
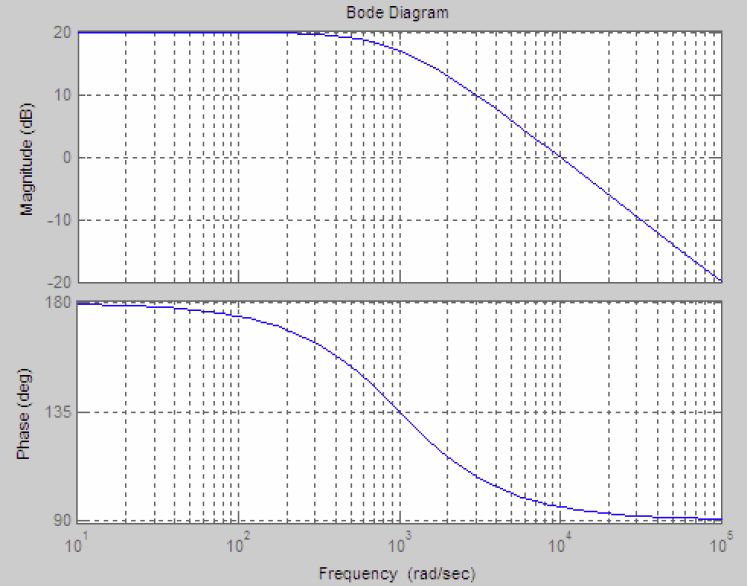
 , the Bode plots are shown
below:
, the Bode plots are shown
below:
Qualitatively, we see that this is a high-pass filter as
 (3)
(3)
 when
when  .
.
Specifically,
 |
 |
 |
|
 |
 |
(4) |
 is the gain when
is the gain when
 ,
,
 is the cut-off or corner frequency, at which
is the cut-off or corner frequency, at which
 . Intuitively, when frequency is
low
. Intuitively, when frequency is
low  is large and the signal is difficult to pass,
therefore the output is low. For example, when
is large and the signal is difficult to pass,
therefore the output is low. For example, when  ,
,
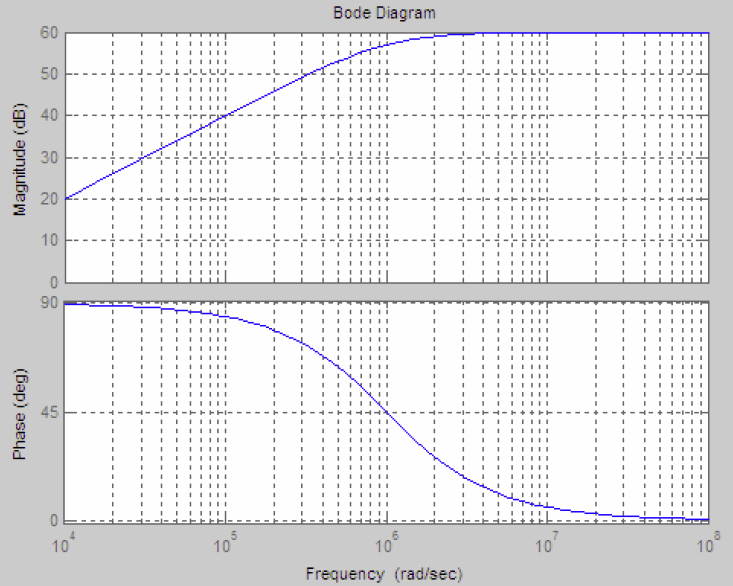
 , the Bode plots are shown below:
, the Bode plots are shown below:
If we let 



 (5)
(5)
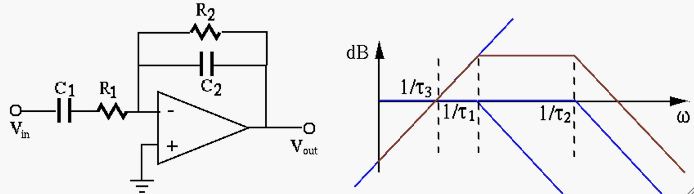
Qualitatively, we see that this is a band-pass filter as
 (6)
(6)
 when
when
 .
.
We let
 (7)
(7)
 |
 |
 |
|
 |
 |
||
 |
 |
||
 |
 |
||
 |
 |
(8) |
 ,
,  ,
,  ,
,
 , and
, and
 .
This is a bandpass filter with the peak at the natural frequency
.
This is a bandpass filter with the peak at the natural frequency
 , which is the geometric average of the two corner frequencies
, which is the geometric average of the two corner frequencies
 and
and
 , or the arithmetic average of
, or the arithmetic average of
 and
and  in log scale:
in log scale:
 (9)
(9)
For example, if





 (10)
(10)
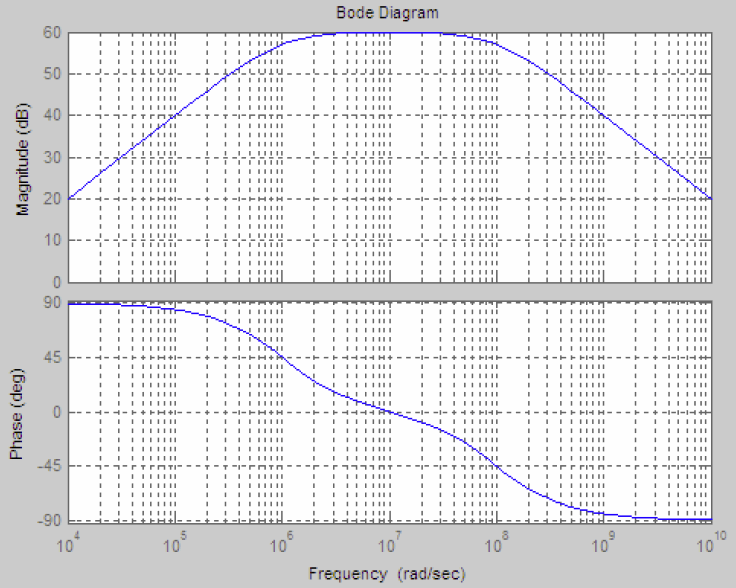
If the log-magnitude 
 (11)
(11)
 and
and  in the op-ammp circuit of the band-pass filter, we get a band-stop filter:
in the op-ammp circuit of the band-pass filter, we get a band-stop filter:
 |
 |
 |
|
 |
 |
(12) |