Metal-Oxide-Semiconductor Field-Effect Transistors

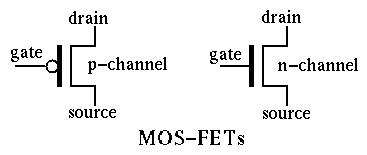
A metal-oxide-semiconductor field-effect transistor (MOSFET) has three terminals, source, gate, and drain. In an n-MOSFET (or p-MOSFET), both the source S and drain D are N-type (or P-type) and the substrate between them is P-type (or N-type). The gate and the P-type substrate is insulated by a thin layer of silicon dioxide ($SiO_2$). Due to this insulation, there is no gate current to either the source or drain.

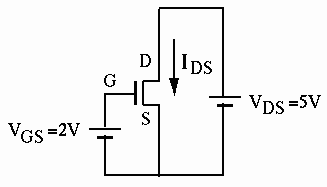
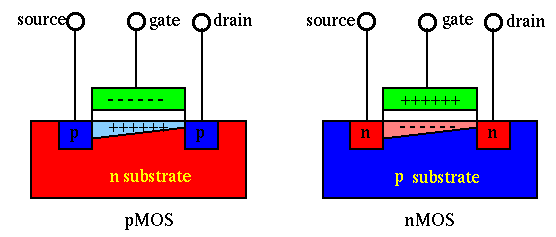
Typically the polarities of the voltages applied to the MOS transistor are such that

$$V_{GS}=V_G-V_S>0 \;\;\;\;\;\;\; \;\;\;\;\;\;V_{DS}=V_D-V_S>0$$ (154)

The n-MOSFET can be considered as a voltage-controlled current channel. When sufficient voltage $V_{GS}$ is applied between gate and source, the positive potential at the gate will induce enough electrons from the P-type substrate (minority carriers) to form an electronic channel called an inversion layer between source and drain, and a current $I_D$ between source and drain is formed.

The MOS transistor can be used in either analog circuits or as a switch in binary logic circuit:

$$\left\{ \begin{array}{l} V_{GS} \uparrow \Longrightarrow I_D \upa... ...ongrightarrow I_D \downarrow \Longrightarrow \mbox{cut off} \end{array} \right.$$ (155)

More acturately, the drain current $I_D(V_{GS})$ as a function of the gate voltage $V_{GS}$ can be modeled by

$$I_D=\left\{ \begin{array}{ll} 0 & \mbox{if $V_{GS}<V_T$\ (cutoff)... ... K(V_{GS}-V_T)^2 & \mbox{if $V_{GS}\ge V_T$\ (conducting)} \end{array} \right.$$ (156)

When the input voltage $V_{GS}$ is lower than the threshold voltage $V_T$, no inversion layer is formed, and no current flows through S and D. When $V_{GS}$ is higher than $V_T$, the current $I_D$ is proportional to the difference squared.

Moreover, the current $I_D$ affected by voltage $V_{DS}$ as well as $V_{GS}$ can be considered as a function $I_D(V_{GS},\,V_{DS})$ of both $V_{GS}$ and $V_{DS}$, as plotted below (similar to a bipolar transistor $I_C=f(I_B,\,V_{CE})$):

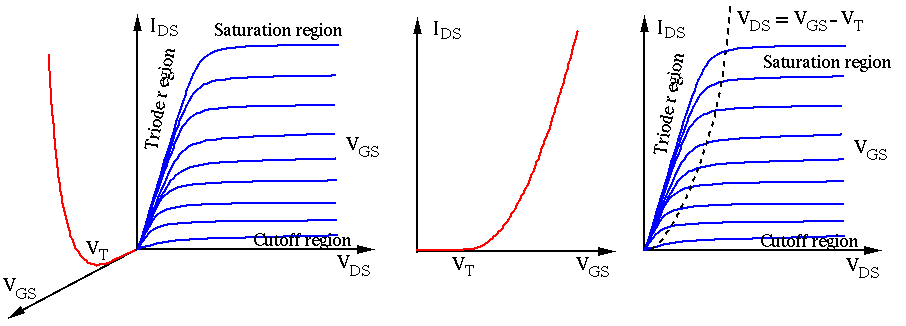
This function can be divided into three different regions:

• Cutoff region:

  $$V_{GS} < V_T,\;\;\;\;\;\; \;\;\;\;\;I_D=0$$ (157)

• Triode region:

  $$V_{GS}>V_T\;\;\;\;\;\; \;\;\;\;\;\;V_{GD}=V_{GS}-V_{DS}>V_T$$ (158)

  Voltages $V_{GS}$ and $V_{GD}$ at both the S and D ends of the inversion layer exceeds $V_T$, some electrons as minority carriers in the P-type substrate are pulled toward the gate to form an inversion layer close to the gate to form an N-type channel with certain resistance between S and D. $I_D$ increases linearly as $V_{DS}$ increases, with a coefficient $\Delta V_{DS}/\Delta I_D$ (Ohm's law), and nonlinearly as $V_{GS}$ increases (to pull more electrons toward the gate to enhance the conductivity of the n-channel). Note that as $V_{GS}>V_{GD}$, the inversion layer is narrower at the D end than the S end.

• Saturation region:

  $$V_{GS}>V_T\;\;\;\;\;\; \;\;\;\;\; V_{GD}=V_{GS}-V_{DS}<V_T$$ (159)

  Voltage $V_{GS}$ at the S end exceeds $V_T$, but $V_{GD}$ at the D end is lower than $V_T$. On the one hand, the increased voltage $V_{DS}$ tends to increase $I_D$, on the other hand, the reduced $V_{GD}$ makes the inversion layer at the D end narrow to the extend that it is nearly closed (pinch-off). As the result, higher voltage $V_{DS}$ does not cause more current $I_D$ (saturated), and it is only affected by $V_{GS}$.

In the plot of $I_D$ vs $V_{DS}$, the triode region and the saturation region are separated by the curve of $V_{GD}=V_{GS}-V_{DS}=V_T$.

Example: Assume $V_T=1V$.

• when $V_{GS}<V_T=1V$, the MOSFET is in cutoff region with $I_D=0$ independent of $V_{DS}$.
• when $V_{GS}=2V > V_T=1V$ and $V_{DS}<V_{GS}-V_T=1V$, the MOSFET is in linear or triode region with $I_D$ affected by both $V_{GS}$ and $V_{DS}$.
• when $V_{DS}>V_{GS}-V_T=1V$, the MOSFET is in saturation region with $I_D$ determined only by $V_{GS}$.

Assume $K=2 mA/V^2$ and $V_T=1V$, and both MOSFETs in the following circuit are in the saturation region. Find $I_D$ and output voltage $V$.

$I_D=K(V_{GS}-V_T)^2=2(2-1)^2=2\,mA$. As both MOSFETs are in saturation region with the same $I_D$ which is determined only by $V_{GS}$ but independent of $V_{DS}$, their $V_{GS}$ must be the same. The upper transistor must have the same $V_{GS}$ as the lower one $V_{GS}=2V$, i.e., the output voltage has to be $5-2=3V$. For the lower transistor, $V_{GD}=V_{GS}-V_{DS}=2-3=-1<V_T=2$, i.e., the transistor is indeed in saturation region.

Comparison between BJT and FET

• BJT has a low input resistance $r_{in}$. But as MOSFET's gate is insulated from the channel ( $r_{in}>10^{11} \Omega$), it draws virtually no input current from the source and therefore has infinite input resistance.
• BJT can be considered as a current amplifier as its output current $I_C$ is proportional ($\beta$ and $\alpha$) to its input current ($I_B$ or $I_E$), but MOSFET is voltage ($V_{GS}$) controlled. Consequently, the power consumption of MOSFETs is lower than BJTs.
• MOSFETs are easy to fabricate in large scale and have higher element density than BJTs.
• MOSFETs have thin insulation layer which is more prone to statics and requires special protection.
• BJTs have higher cutoff frequency and higher maximum current than MOSFETs.
• MOSFETs are much more widely used than BJTs (especially in computers and digital systems).
• Both majority and minority carriers are used in BJTs, but only majority carriers are used in FETs. Consequently FETs have better temperature stability (minority carriers are more sensitive to temperature).

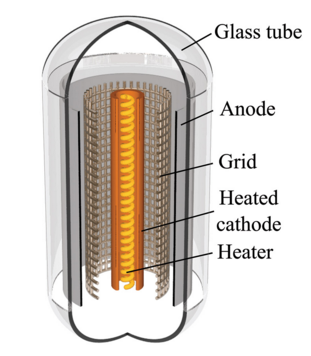
The BJT and FET can be compared with the old technology of vacuum tube based on thermionic electron emission (heated filament). Although the specific physics of each of these devices is quite different from others, the working principles of these devices are essentially the same. In all three devices, a small AC input voltage (signal) is applied to the input terminal of the device (base, gate, or grid) to control the current that flows through the device (from collector, drain, or anode to emitter, source, or cathode, respectively), causing a much amplified voltage to appear at the output terminal (collector, drain, or anode) of the device.