Consider an RC circuit consisted of a resistor and a capacitor in
series connected to an AC voltage source
 , find
the voltage
, find
the voltage  across
across  . The governing DE describing the circuit
can be obtained based on KVL:
. The governing DE describing the circuit
can be obtained based on KVL:
 |
(73) |
When the external input is zero  , the DE is homogeneous
(zero on the right-hand side):
, the DE is homogeneous
(zero on the right-hand side):
 |
(74) |
The non-trivial solution of this homogeneous equation is due to some
non-zero initial value, the voltage
 across the capacitor before
across the capacitor before  . The homogeneous solution needs to
be a function whose derivative takes the same form as the function
itself, an exponential function:
. The homogeneous solution needs to
be a function whose derivative takes the same form as the function
itself, an exponential function:
 and and |
(75) |
Substituting them into the DE, we get
 |
(76) |
As we are not interested in the trivial solution  , we must
have
, we must
have
 i.e. i.e. |
(77) |
Now we get
 for
for  . The constant coefficient
. The constant coefficient
 can be obtained by the initial condition
can be obtained by the initial condition
 :
:
 i.e. i.e. |
(78) |
Now the homogeneous solution is found to be
 |
(79) |
which decays to zero as
 :
:
 |
(80) |
The same result can also be obtained by the
Laplace transform method.
The current through  and
and  is
is
 |
(81) |
The voltage across  is
is
 |
(82) |
This result can be verified by KVL:
 .
.
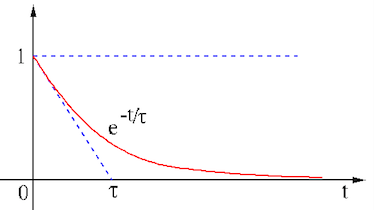
The time constant  can be identified on the time plot of the general
first order response
can be identified on the time plot of the general
first order response
 with
with  . Specifically
consider the derivative of
. Specifically
consider the derivative of  evaluated at
evaluated at  :
:
 |
(83) |
This is the slope of the tangent line of  at
at  , and
, and  is its
intersection with the horizontal axis. We conclude that the voltage across a
capacitor cannot change instantaneously due to the time constant
is its
intersection with the horizontal axis. We conclude that the voltage across a
capacitor cannot change instantaneously due to the time constant  ,
unless
,
unless  and therefore
and therefore  . (The same can be said for the current
through an inductor.)
. (The same can be said for the current
through an inductor.)




 , the DE is homogeneous
(zero on the right-hand side):
, the DE is homogeneous
(zero on the right-hand side):

 across the capacitor before
across the capacitor before  . The homogeneous solution needs to
be a function whose derivative takes the same form as the function
itself, an exponential function:
. The homogeneous solution needs to
be a function whose derivative takes the same form as the function
itself, an exponential function:
 and
and

 , we must
have
, we must
have
 i.e.
i.e.
 for
for  . The constant coefficient
. The constant coefficient
 can be obtained by the initial condition
can be obtained by the initial condition
 :
:
 i.e.
i.e.
 :
:




 is
is

 .
.






 at
at  , and
, and  is its
intersection with the horizontal axis. We conclude that the voltage across a
capacitor cannot change instantaneously due to the time constant
is its
intersection with the horizontal axis. We conclude that the voltage across a
capacitor cannot change instantaneously due to the time constant  ,
unless
,
unless  and therefore
and therefore  . (The same can be said for the current
through an inductor.)
. (The same can be said for the current
through an inductor.)
