Phasor Representation of Sinusoidal Variables

In the following discussion about AC circuit analysis, all sinusoidal variables (currents and voltages) are assumed to be of the same frequency. In general, arithmetic operations of sinusoidal functions are not convenient as they will involve using trigonometric identities. For example, given two sinusoids of the same frequency $\omega$:

$$\left\{ \begin{array}{l} x(t)=A\cos(\omega t+\phi)\\ y(t)=B\cos(\omega t+\psi) \end{array} \right.$$ (16)

we can find their sum as:

$$z(t)=x(t)+y(t) = A\cos(\omega t+\phi)+B\cos(\omega t+\psi)$$

$$= A\cos\omega t\cos\phi-A\sin\omega t\sin\phi +B\cos\omega t\cos\psi-B\sin\omega t\sin\psi$$

$$= (A\cos\phi+B\cos\psi) \cos\omega t -(A\sin\phi+B\sin\psi)\sin\omega t$$ (17)

If we further assume

$$\left\{\begin{array}{l} A\cos\phi+B\cos\psi=C\cos\theta=C_r\\ A\sin\phi+B\sin\psi=C\sin\theta=C_i \end{array}\right.$$ (18)

then $z(t)$ above can be written as the following in terms of $C$ and $\theta$:

$$z(t)=C\cos\theta \cos\omega t+C\sin\theta \sin\omega t =C \cos(\omega t+\theta)$$ (19)

To find $C$ and $\theta$ we note that

$$\left\{\begin{array}{l} C_r^2+C_i^2=C^2\\ \\ C_i/C_r=\tan\theta \end{array}\right.$$

and solve these equations to get

$$C=\sqrt{C_r^2+C_i^2},\;\;\;\;\;\;\;\;\;\;\; \theta=\tan^{-1} (C_i/C_r)$$ (20)

Alternatively, the addition of the two sinusoidal functions above can also be carried out when they are treated as the real (or imaginary) parts of rotating vectors in the complex plane, and thereby more conveniently added in vector forms in the complex plane:

$$z(t)=x(t)+y(t) = A\cos(\omega t+\phi)+B\cos(\omega t+\psi)$$

$$= Re(A e^{j(\omega t+\phi)})+Re(B e^{j(\omega t+\psi)})$$

$$= Re[(A e^{j\phi}+B e^{j\psi})e^{j\omega t}]$$ (21)

We can get $z(t)$ in three steps:

• add the two complex exponentials $A e^{j\phi}$ and $B e^{j\psi})$ as two vectors (not rotating) in the complex plane;
• multiply $e^{j\omega t}$ (rotate again);
• take the real part.

Here the two complex exponentials $A e^{j\phi}$ and $B e^{j\psi}$ are called the phasors of the sinusoidal functions $x(t)$ and $y(t)$.

• Represent a sinusoidal time function $x(t)$ into a phasor $\dot{X}$ (transformation from time domain to frequency domain):

  $$x(t)=A\cos(\omega t+\phi) =Re \left( A e^{j(\omega t+\phi)}\right... ...left( A e^{j\phi} e^{j\omega t} \right) =Re\left( \dot{X} e^{j\omega t} \right)$$ (22)

  where $\dot{X}=A e^{j\phi}$ is the phasor representation of $x(t)=A\cos(\omega t+\phi)$, a vector in the complex plane.

• Convert a phasor $\dot{X}$ back into a sinusoidal time function $x(t)$ (transformation from frequency domain to time domain):

  $$Re\left( \dot{X} e^{j\omega t} \right) =Re\left( A e^{j\phi}\; e^{j\omega t} \right) =A\cos(\omega t+\phi)$$ (23)

  When multiplied by $e^{j\omega t}$, the phasor vector $\dot{X}$ starts to rotate in CCW direction, and its projection onto the real axis is a real sinusoidal function.

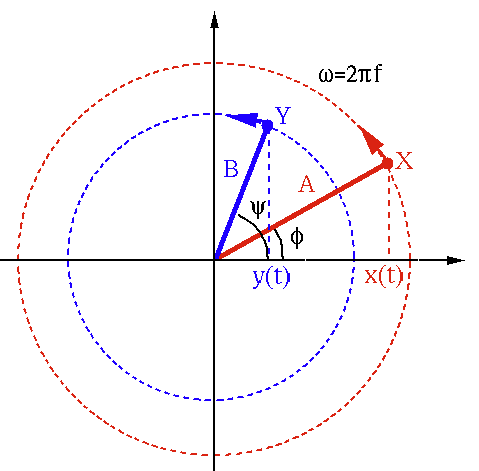
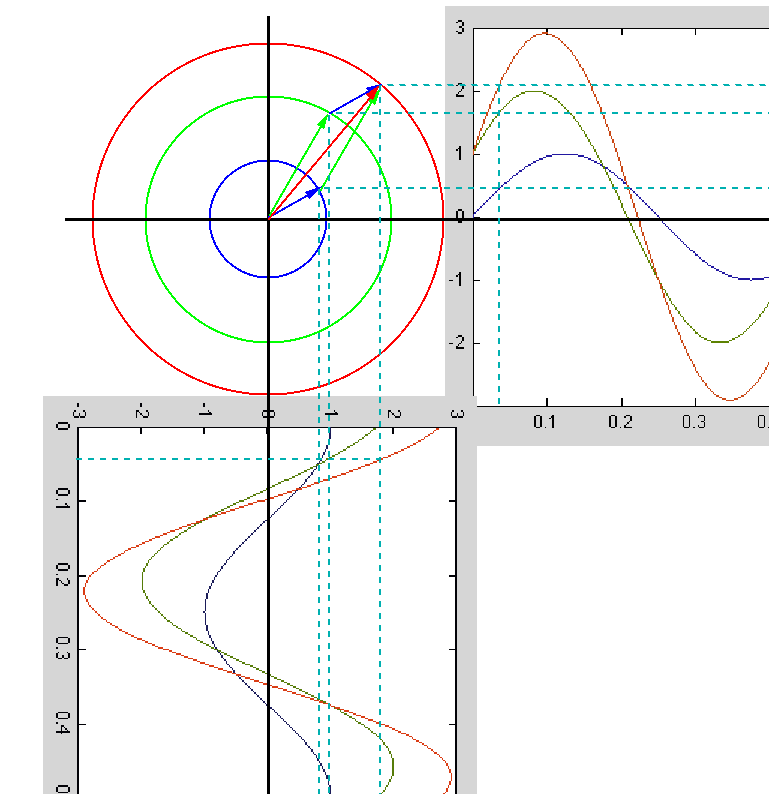
Specifically, the sum $z(t)=x(t)+y(t)$ of the two sinusoidal functions once represented in phasor form in complex plane can be found as the real part of the vector sum in the following three steps:

• Represent both sinusoids by their corresponding phasors

  $$\left\{ \begin{array}{l} x(t)=A\cos(\omega t+\phi)=Re[A e^{j\phi}... ...psi)=Re[B e^{j\psi}e^{j\omega t}] =Re[\dot{Y}e^{j\omega t}] \end{array} \right.$$ (24)

  where

  $$\dot{X}=Ae^{j\phi}=A\;\angle\phi, \;\;\;\;\;\;\;\;\;\;\;\dot{Y}=Be^{j\psi}=B\;\angle\psi$$ (25)

  are the phasors represented as vectors in the complex plane in terms of their magnitudes and initial phases.
• Find the phasor $\dot{Z}$ of the sum $z(t)=x(t)+y(t)$ as the vector sum of the two phasors (carry out operation in frequency domain):
  

  $$\dot{Z}=\dot{X}+\dot{Y} = Ae^{j\phi}+Be^{j\psi} =(A\cos\phi+j\,A\sin\phi)+(B\cos\psi+j\,B\sin\psi)$$

  $$= (A\cos\phi+B\cos\psi)+j\,(A\sin\phi+B\sin\psi)$$

  $$= C_r+j\,C_i=C e^{j\theta}$$ (26)

  
  where

  $$\left\{\begin{array}{l} C_r=A\cos\phi+B\cos\psi\\ C_i=A\sin\phi+B... ...n{array}{l} C=\sqrt{C_r^2+C_i^2}\\ \theta=\tan^{-1}(C_i/C_r) \end{array}\right.$$ (27)

• Get the time function $z(t)$ by multiplying its phasor $\dot{Z}$ by $e^{j\omega t}$ and taking its real part

  $$z(t)=Re\left(\dot{Z}e^{j\omega t}\right) =Re\left(Ce^{j\theta}e^{j\omega t}\right) =Re\left(Ce^{j\omega t+\theta}\right) =C\cos(\omega t+\theta)$$ (28)

(review of complex arithmetic)

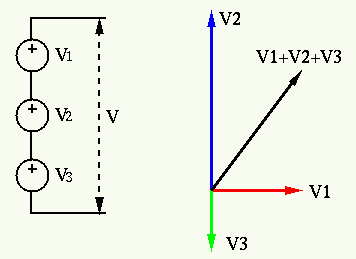
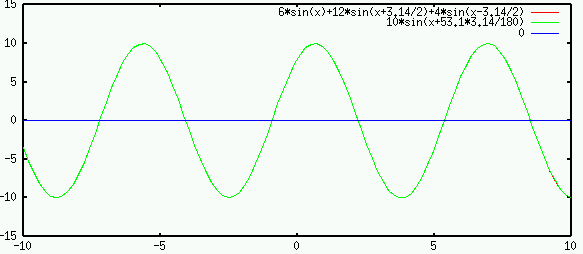
Example

Consider three sinusoidal voltage sources $v_1(t)=6\;\sin(\omega t)$, $v_2(t)=12\;\sin(\omega t+\pi/2)$ and $v_3(t)=4\;\sin(\omega t-\pi/2)$ in series. According to the KVL, the overall voltage will be the algebraic sum of the three:

$$v(t)=v_1(t)+v_2(t)+v_3(t) =6\;\sin(\omega t)+12\;\sin(\omega t+\pi/2) +4\;\sin(\omega t-\pi/2)$$ (29)

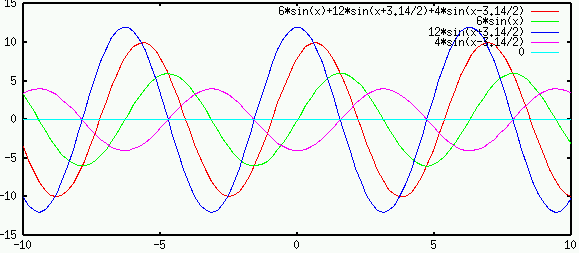
While the addition of these sinusoidal functions is not easy to carry out (still remember all the trigonometric identities?), it is quite straight forward to find the vector sum if the voltages are represented as phasors:

$$\dot{V} = \dot{V}_1+\dot{V}_2+\dot{V}_3 =6\angle 0^\circ+12\angle 90^\circ+4\angle -90^\circ$$

$$= 6+j8=10 \angle \left[\tan^{-1}(8/6)\right] =10\angle\; 53.1^\circ$$ (30)

The resulting voltage is $v(t)=10\;sin(\omega t+53.1^\circ)$

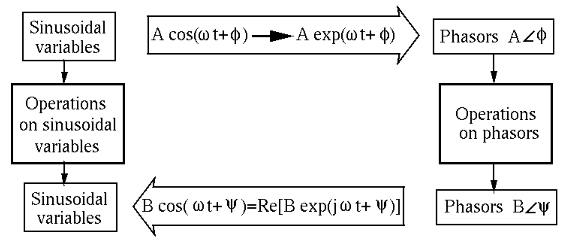
Phasor and the Fourier transform

A sinusoidal function $x(t)=A\cos(\omega t+\phi)$ can be expressed in either Fourier transform (Fourier series) or phasor representation:

$$x(t) = A\cos(\omega t+\phi)=Re[Ae^{j\phi}\;e^{j\omega t}]=Re[\dot{X} e^{j\omega t}]$$

$$= \left(\frac{A}{2}e^{j\phi}\right)e^{j\omega t} +\left(\frac{A}{2}e^{-j\phi}\right)e^{-j\omega t} =X_1 e^{j\omega t}+X_{-1}e^{-j\omega t}$$ (31)

where

$$\dot{X}=Ae^{j\phi},\;\;\;\;\;\;\;\;\;\;\;\;\;\; X_1=\frac{A}{2}e^{j\phi},\;\;\;X_{-1}=\frac{A}{2}e^{-j\phi}$$ (32)

We see that the phasor $\dot{X}$ and the Fourier coefficients $X_1$ and $X_{-1}$ are essentially the same, in the sense that they are both coefficients representing the amplitude and phase of the complex exponential function $e^{j\omega t}$.

In both cases the real time function can be obtained (inverse Fourier transform) by either adding the two complex vectors $X_1e^{j\omega t}$ and $X_{-1}e^{-j\omega t}$ rotating in opposite directions (CCW and CW), or simply taking the real part of the complex variable $\dot{X}e^{j\omega t}$