Review of Complex Arithmetic

A complex number can be represented in two different formats in either the Euclidean and polar coordinate system:

• Euclidean representation:

  $z=x+jy$ where $x$ and $y$ are the real (horizontal) and imaginary (vertical) part of complex variable $z$, respectively.

• Polar representation:

  $z = \vert z\vert\;e^{j\angle z}$, or simply $z=\vert z\vert\;\angle z$, where $\vert z\vert$ and $\angle z$ are the magnitude and phase angle, respectively.

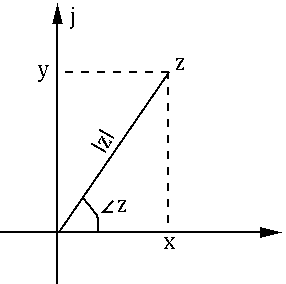
The two representations can be converted from one to the other:

• From $(x,y)$ to $(\vert z\vert,\angle z)$:

  $$\left\{ \begin{array}{ll} \vert z\vert=\sqrt{x^2+y^2} & \mbox{magnitude}\\ \angle z=\tan^{-1} (y/x) & \mbox{phase angle} \end{array} \right.$$ (463)

• From $(\vert z\vert,\angle z)$ to $(x,y)$:

  $$z=\vert z\vert\;e^{j\angle z}=\vert z\vert(\cos\angle z+j\;\sin\angle z)=x+jy$$ (464)

  due to Euler identity, i.e.,

  $$\left\{ \begin{array}{ll} x=\vert z\vert\;\cos\angle z & \mbox{re... ...rt}\\ y=\vert z\vert\;\sin\angle z & \mbox{imaginary part} \end{array} \right.$$ (465)

The arithmetic operations of two complex numbers $z=x+jy=\vert z\vert\;e^{j\angle z}$ and $w=u+jv=\vert w\vert\;e^{j\psi}$ are listed below:

• Add/Subtract:

  $$z+w=(x+u)+j(y+v),\;\;\;\;z-w=(x-u)+j(y-v)$$ (466)

• Multiply:

  $$z\;w=(x+jy)(u+jv)=(xu-yv)+j(xv+yu)=\vert z\vert\;\vert w\vert\;e^{j(\angle z+\angle w)}$$ (467)

• Divide:

  $$\frac{z}{w}=\frac{x+jy}{u+jv}=\frac{(x+jy)(u-jv)}{(u+jv)(u-jv)} =... ...j(yu-xv)}{u^2+v^2} =\frac{\vert z\vert}{\vert w\vert}\;e^{j(\angle z-\angle w)}$$ (468)

• Rotation:

  When a complex number, a vector in complex plane, $z = \vert z\vert\;e^{j\angle z}$ is multiplied by $e^{j\alpha}$, it becomes $z\;e^{j\angle z}=\vert z\vert\;e^{j(\angle z+\alpha)}$, i.e., rotated by an angle of $\alpha$. The rotation is counter-clock wise if $\alpha>0$, but clock-wise if $\alpha<0$. When the rotating angle is a linear function of time $\alpha=\omega t$, then vector $z=\vert z\vert\;e^{j(\angle z+\omega t)}$ becomes a rotating vector with angular frequency $\omega$.

  In particular, As $e^{j\pi/2}=j$ and $e^{-j\pi/2}=-j$, they can be considered as $90^\circ$ rotation factors. Any complex number multiplied by $j$ or $-j$ will be rotated counter clockwise or clockwise by 90 degrees.

• Complex Conjugate:

  The complex conjugate of $z=x+jy=\vert z\vert e^{j\angle z}$ is $z^*=x-jy=\vert z\vert e^{-j\angle z}$. In general, $z^*$ can be obtained by negating every $j$ in the expression of $z$ (replacing $j$ by $-j$). The magnitude of a complex number $z=x+jy$ can be found by:

  $$\sqrt{zz^*}=\sqrt{(x+jy)(x-jy)}=\sqrt{x^2+y^2}=\vert z\vert$$ (469)

• Reciprocal:

  $$\vert z^{-1}\vert=\frac{1}{\vert z\vert}=\frac{1}{\sqrt{x^2+y^2}}... ...\angle\left(z^{-1}\right)=\angle\left(\frac{1}{z}\right) =0-\angle{z}=-\angle z$$ (470)